一类四阶非线性Schrödinger方程解的整体适定性
祝佳玲, 米彩莲, 杨 晗
(西南交通大学数学学院,四川成都611756)
本文研究非线性Schrödinger方程的初边值问题

其中,u=u(t,x)是复值函数,p>0 为常数,Ω⊂R4为边界充分光滑的有界区域,n为方向向量.
Schrödinger方程是量子力学的基本方程,它描述了微观粒子的局域特征和波-粒二象性,考查了在非线性系统中粒子之间的相互作用.对于非线性Schrödinger方程,已有许多作者进行了广泛的研究[1-13],其中 Brezis等在文献[1]中考虑了二阶非线性 Schrödinger方程

的初边值问题,其中,p=2,Ω⊂R2,且具有紧的光滑边界.采用的方法是借助半群理论、能量估计及B-G型不等式,建立了相应的先验估计,得到问题(2)的经典解的整体存在性.事实上,对于0<p≤2,采用同样的方法,可以证明文献[1]中的结论均成立.Tsutsumi[2]研究了文献[1]的推广情形,即研究了如下的非线性Schrödinger方程的初边值问题

其中,Ω⊂R2是有界域,边界光滑有界,f:R+→R 是(0,∞)上的 C2函数,满足

p∈[1,∞ ),Ci是常数.文献[2]建立了新的 B-G型不等式,证明了当2≤p≤3时光滑解的整体存在性.本文采用以上方法研究四阶非线性Schrödinger方程的初边值问题.
文献[1]中B-G型不等式是对经典的Sobolev不等式Hs嵌入到L∞(n为空间维数)情形的改进,即把由线性增长控制减弱为由对数增长控制.本文采用了这一改进,方法即引用B-G型不等式,借助Galerkin方法,得到解的整体适定性,并利用Gronwall不等式证明了解的唯一性.
1 解的整体适定性
本文采用的方法是Galerkin方法,其过程是常规步骤的实施,本文只给出解的相应先验估计.
为了得到解的相应先验估计,准备工作如下.
引理 1.1[4](B-G 型不等式) 设 Ω⊂R4为边界充分光滑的有界域,u∈(Ω),其中 σ≥2,且‖u1,则存在常数 C,使得不等式成立.
对于引理1.1,取 n=4,σ =3,则有更精细的B-G型不等式

对任意的 u∈H4(Ω),且‖u‖H2(Ω)≤1.
引理 1.2[5](Gagliardo-Nirenberg 不等式)设Ω为光滑有界域,j、m是整数,p为实数θ≤1,且0≤j<m,1≤q,r≤∞,则当
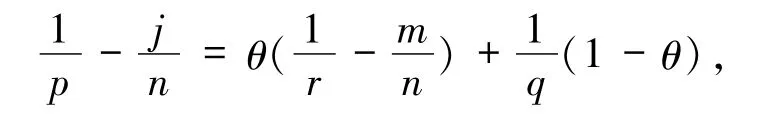
对任意 u∈Wm,r(Ω)∩Lq(Ω),存在正常数 C1和C2,使得
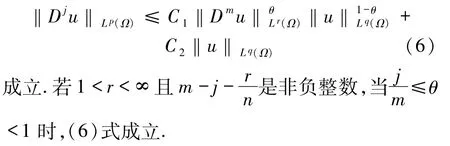
引理 1.3 令 u =u(x,t)是问题(1)的光滑解,则有质量守恒
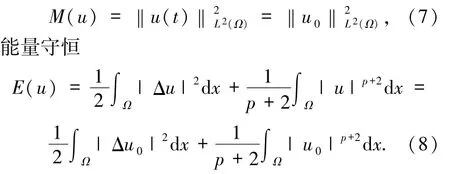
证明 对方程(1)与¯u作内积,考虑其虚部,则有

故(7)式成立.


C是与初值有关的正常数.
引理 1.4 令 u =u(x,t)是问题(1)的光滑解,则有

由于 H2(Ω)嵌入到 L2(p+1)(Ω),所以(10)式成立.
引理 1.5 令 u =u(x,t)是问题(1)的光滑解,且 p≥1,则有

其中C为常数.



由Sobolev嵌入定理及引理1.4得

由(14)~(16)式得(13)式成立.
若把工作空间定义为 X={u|u∈H6(Ω)∩(Ω),Δ2u∈(Ω)},则有如下定理.
定理1.7 假设1≤p≤5,且 Ω⊂R4为充分光滑的有界区域,对任意的u0∈X,则对任意的T>0,方程(1)存在唯一解 u =u(x,t),使得

利用方程(1),分别对(17)式两边作估计有:
第一项

其中C为常数.
令 G(u)= ‖Δut‖L2(Ω),将不等式化作方程,并对两边关于时间t求导,得

即 1≤p≤5.
由方程(1)易得

下证唯一性.设 u1、u2为方程(1)的2 个解,令w=u1-u2,则w满足下列方程


其中C为常数.因此,唯一性得证.

