max-*合成模糊关系方程的解集
朱晓庆, 熊清泉
(四川师范大学数学与软件科学学院,四川成都610066)
模糊关系在模糊系统中占有比较重要的地位,模糊关系方程为模糊关系的主要研究对象之一.1976 年,Sanchez[1]首先讨论了 max-min 合成有限模糊关系方程,给出了方程有解的判定定理,并且在有解情况下给出了最大解的公式.之后,大量的研究者从不同合成算子、不同论域、不同算法等方向来研究模糊关系方程[2-10].值得注意的是,Zhao[11]在完备分配格上讨论了矩阵方程,当格中每个元都有不可约有限并(交)既分解时,给出了方程可解的充要条件,并且在方程可解时,进一步给出方程的解集.1989年,Di Nola等[12]讨论了完备Brouwer格上max-min合成模糊关系方程,给出了方程有解的充要条件.De Baets[13-14]讨论了完备分配格上的sup-T合成模糊关系方程,其中T为t-模.Fodor等[15]证实非交换、非结合算子在近似推理中更有效.2005年,Wang等[9]讨论了完备格上的sup-T合成模糊关系方程,其中T为伪t-模(非交换、非结合),给出了方程有解的充要条件以及存在极小解的充分条件,获得了相应的解集结构.事实上,在求解sup-T(T代表t-模或伪t-模算子)合成模糊关系方程时,求极小解是其中的关键.针对不同合成算子,研究者给出了不同求极小解的方法.Lin[4]用覆盖方法研究了max-Archimedean t-模合成模糊关系方程,发现此类方程与无冗余覆盖存在一一对应关系.Han等[3]在方程有解时根据最大解构造有限偏序集,进一步求出方程的极小解.Matusiewicz等[16]在求解max-*合成模糊关系方程时,通过诱导矩阵首先求出不等式的极小解,进而得到方程的极小解.本文在文献[16]基础上不引入诱导矩阵,讨论[0,1]上max-*合成模糊关系方程.首先讨论单个变量方程,给出方程有解的充要条件.然后讨论多变量单一方程,给出方程解集非空的充要条件.在解集非空时,进一步给出方程存在极小解的必要条件以及极小解的个数.最后讨论方程组的解集,给出方程组解集非空的充要条件,并且在方程组解集非空时,利用最大解构造有限偏序集的方法给出方程组的极小解,进一步给出方程组的解集.
1 预备知识
设 I = {1,2,…,m},J = {1,2,…,n}.向量 x= (xj)j∈J,y = (yj)j∈J,矩阵 A = (aij)I×J,B =(bij)I×J,其中,xj,yj,aij,bij∈ L = [0,1].定义序关系≤为 x≤y⇔xj≤yj,A ≤ B⇔aij≤bij,∀i∈ I,j∈ J.
考虑方程


其中“◦”代表 max-*合成运算,矩阵 A = (aij)m×n与向量 B = (bi)i∈I已知,X = (xj)j∈J未知.
定义 1.1[17]设T :L ×L→L满足:∀a,b,c∈L,有
(i)交换律:T(a,b)= T(b,a);
(ii)结合律:T(a,T(b,c))= T(T(a,b),c);
(iii)单调性:如果 b≤c,则T(a,b)≤T(a,c);
(iv)有界性:T(a,1)= a,称T是(L,≤)上的三角模(简称t-模).
定义1.2[18]设Γ:L ×L→L满足:∀a,b,c∈L,
(i)单调性:如果b≤c,则Γ(a,b)≤Γ(a,c);
(ii)边界条件:Γ(1,a)= a且 Γ(0,a)= 0,称Γ是(L,≤)上的伪t-模.如果Γ还满足Γ(a,0)=0,则称Γ为强伪t-模.
定义 1.3[17]设二元运算*:L × L →L,如果对任意单调不减的序列{xn}n∈N都有(xn*y))*y,∀y∈L,则称二元运算*是左连续的.类似可定义右连续,如果*既是左连续的也是右连续的,则称*是连续的.
定义 1.4[16]设*:L ×L→L 满足:∀a,b,c∈L,
(i)单调性:如果 b≤ c,则 a*b≤ a*c;
(ii)边界条件:1*0 =0;
(iii)连续性:既是左连续的也是右连续的,称*是(L,≤)上的*运算.(L,≤)上的全体*运算用LRC表示.
定义 1.5[19]设φ:L × L→L,定义→φ与←φ为:∀a,b∈ L,

假定空集的上确界是0,下确界为1.特别地,当φ=*时,二元运算→*:L×L→L称为诱导蕴涵,即

当φ=*时,二元运算←*:L×L→L称为对偶诱导蕴涵,即

定义 1.6[20]设二元运算*:L × L → L,如果* 满足:∀a,bλ∈ [0,1],λ ∈ Λ(Λ ≠ Ø),
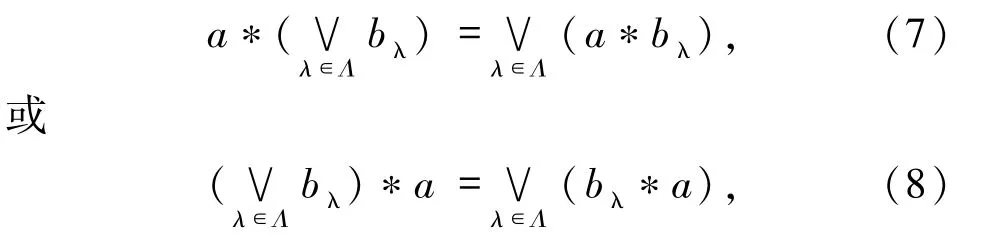
则称*是左(右)无限∨-分配的.如果*既是左无限∨-分配的,又是右无限∨-分配的,则称*是无限∨-分配的.类似地,如果*满足:

则称*是左(右)无限∧-分配的.如果*既是左无限∧-分配的,又是右无限∧-分配的,则称*是无限∧-分配的.如果*既是无限∧-分配的,又是无限∧-分配的,则称*是无限分配的.
引理 1.1[15]设*:L × L→L单调递增,则二元运算*是连续的当且仅当*是无限分配的.
引理 1.2[15]设 {t∈L:a*t≤b}≠Ø,∀a,b∈L.如果单调递增的二元运算*:L×L→L关于第二变元左连续,则L上诱导蕴涵(5)式存在.
引理 1.3[15]设 {t∈L:a*t≤b}≠Ø,∀a,b∈L.如果单调递增的二元运算*:L×L→L关于第二变元右连续,则L上对偶诱导蕴涵(6)式存在.
引理 1.4[19]设二元算子*:L×L→ L为单调递增运算,a,b∈L且诱导蕴涵(5)式存在,则
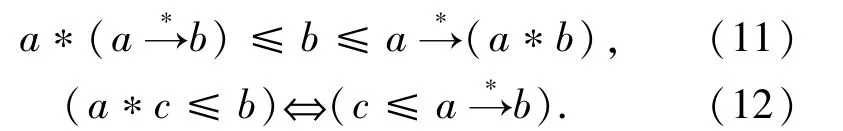
如果对偶诱导蕴涵(6)式存在,则
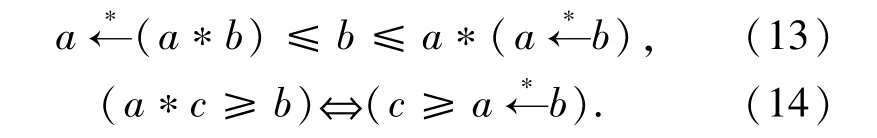
引理1.5[21]如果二元运算*是单调递增的,则max-*合成运算也是单调递增的,即

定义 1.7[22]设(P,≤)是偏序集且 Ø ≠X⊆P.如果p∈X满足x≤p,∀x∈X有p=x,称元素p为X的一个极小元;如果g∈X满足x≤g,∀x∈X,称g为X的一个最大元.
注1.1 方程解集中的极小元称为方程的极小解,方程解集中的最大元称为方程的最大解.
2 方程A◦X=B的解集
本节若未特别说明,则假设*∈LRC,a,b∈L.记 S(a,b,*)= {x ∈ L:a*x = b},S ≤ (a,b,*)= {x∈L:a*x∈b},S≥(a,b,*)= {x∈L:a*x≥b},S(A,B,*)= {X:A◦X = B},S0(A,B,*)表示方程(1)的所有极小解构成的集合,即S0(A,B,*)= {X:X为S(A,B,*)的极小元}.对方程 a*x = b,a,b,x∈L.显然方程a*x = b的解集为

引理 2.1[23]设二元运算*单调递增,X,Y∈S(A,B,*)且 X ∈ Y,则[X,Y]⊆ S(A,B,*).
引理 2.3 S≥(a,b,*)≠Ø当且仅当1∈S ≥ (a,b,*).
证明 ⇐ 显然.
⇒ 设x∈S≥ (a,b,*),则由引理1.5知,a*1 ≥ a*x≥ b.所以1 ∈ S≥ (a,b,*).
证明 ⇐ 显然.
⇒ 设x0∈S(a,b,*),则a*x0= b≤b.由(5)式知,x0≤.又由引理1.5得,b = a*x0≤a*()≤ b.所以,a*()= b,即为方程的解.又因为x0≤,故为方程的最大解.
定理 2.5 如果 S(a,b,*)≠ Ø,则 S(a,b,*)= [].
证明 设x0∈S(a,b,*),由定理2.4得为方程的最大解.又a*x0=b≥b,由(6)式知,x0≥.由引理1.5 得

例 2.1 设 x*y = x·min(x,y),其中 x,y ∈[0,1].考虑方程a*x = b,其中a = 0.8,b = 0.64.
由(5)和(6)式知,

接下来考虑方程

其中“◦”代表max-*合成运算.记S(a,b,*)={x = (xj)j∈J∈Ln:a◦xT= b},S0(a,b,*)= {x:x为 S(a,b,*)的极小元.令

引理2.6 方程(17)有解当且仅当存在j0∈J使得aj0*=b.
证明 ⇐ 显然.
⇒ 设 x = (x1,x2,…,xn)T∈ S(a,b,*),则 ∨j∈J(aj*xj)= b.由于J为有限集,则存在j0∈ J使得aj0}*xj0= b.又由引理1.5及定理2.4知,b=aj0*xj0≤=aj0*()≤b.所以,=b.
令J={j∈J:aj*j=b},可得如下结论.
定理 2.7 如果 S(a,b,*)≠ Ø,则 ∀j0∈J,方程(17)有极小解 x0(j0)= ()j∈J,其中

推论 2.1 如果S(a,b,*)≠Ø,则方程(17)的极小解个数等于 |J|,其中|{·}|表示集合|{·}|的元素个数.
定理 2.8 如果 S(a,b,*)≠ Ø,则 ∀x∈S(a,b,*)存在 x0= ()j∈J∈ S0(a,b,*)使得x0≤ x.
证明 因为 x = (xj)j∈J∈ S(a,b,*),则(aj*xj)= b.由于 J为有限集,则存在j0∈ J使得aj0*xj0= b.又由定理2.5 知xj0∈S(aj0,b,*)=].令

显然x0≤x.又由定理2.7知,x0= ()j∈J为方程的极小解.
定理 2.9 如果 S(a,b,*)≠ Ø,则 S(a,b,*)= ∪x0∈S0(a,b,*)[x0,x¯],其中[x0,x¯]={x∈Ln:x0≤x≤x¯},∀x0∈S0(a,b,*).

另一方面,对 ∀x∈∪x0∈S0(a,b,*)[¯],因为方程(17)的极小解个数等于|J|,为有限集,则存在y0∈S0(a,b,*)使得x∈ [¯].又由引理2.5知,b=a◦y0≤a◦x≤a◦=b,故a◦x=b,即 x ∈ S(a,b,*).因此

例 2.2 考虑方程(0.75,0.8,0.1,1)◦(x1,x2,x3,x4)T= 0.64,其中 * 使用例2.1 中的运算.因为=(1,1,1,0.64)T,经检验,∈S(a,b,*).又因为J = {2,4}且= 0.8,= 0.64,所以方程有 2 个极小解,分别为 x1= (0,0.8,0,0)T,x2= (0,0,0,0.64)T.因此,方程的解集为
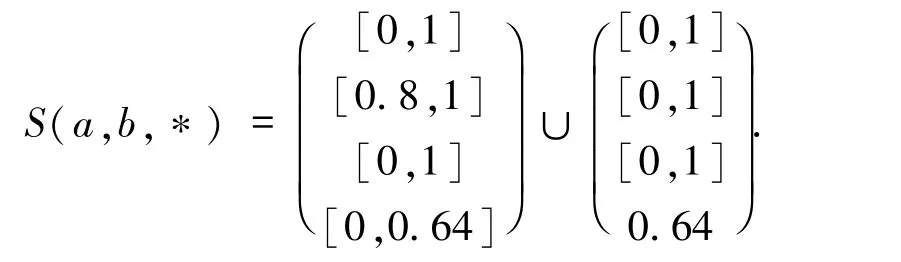
定理2.10 S(A,B,*)≠Ø当且仅当˜X是方程(1)的解.进一步,˜X为方程(1)的最大解.
证明 ⇐ 显然.

下面讨论方程(1)的极小解.
定理 2.11 设 S(A,B,*)≠ Ø,X = (xj)j∈J∈ S(A,B,*),则存在 j0∈ J使得 aij0*xj0= bi,∀i∈ I.
定理 2.12 如果 X ∈ S(A,B,*)且 f∈J(X),则 X(f)≤ X.
定理 2.13 如果X∈S(A,B,*),则F(X)⊆S(A,B,*).

定理 2.14 如果 X,Y ∈ S(A,B,*),X ≤ Y,X(f)∈ F(X),则 f∈ J(Y)且 X(f)= Y(f)∈ F(Y).
证明 设X = (xj)j∈J,Y = (yj)j∈J,且X≤Y.如果 f = (fi)i∈I∈ J(X),则 ∀i∈ I,bi= aifi*xfi≤ aifi*yfi≤bi,即aifi*yfi= bi.因此,fi∈Ji(Y)即 f = (fi)i∈I∈ J(Y).故 X(f)= Y(f)∈ F(Y).
设P是任意一个偏序集,记P的所有极小元构成集合P0.
引理2.15[24]设P为一个偏序集且Ø≠Q⊆P.如果对∀p∈P,∃q∈Q,使得q≤p,则P0= Q0.
引理 2.16 方程(1)的解集 S(A,B,*)与有限偏序集F(˜X)有相同的极小解集.即S0(A,B,*)=F(˜X)0.
证明 由定理2.13知,F(˜X)⊆S(A,B,*).若S(A,B,*)=Ø,则S0(A,B,*)=F(˜X)0=Ø.若S(A,B,*)≠Ø,设X∈S(A,B,*),则由定理2.10知,X≤˜X.由定理2.14及X(f)∈F(X)可得X(f)=˜X(f)∈F(˜X).又由定理2.12知,X(f)≤X.所以,由引理2.15知,S0(A,B,*)=F(˜X)0≠Ø.因此S0(A,B,*)=F(˜X)0.
定理 2.17 如果S(A,B,*)≠Ø,则S(A,B,*)=[X0,X˜],其中[X0,X˜]= {X∈Ln:X0≤X≤X˜,∀A0∈F(X˜)0.
证明 设 X ∈ S(A,B,*),由定理2.16 的证明知,存在Y∈F(X˜)使得Y≤X.又因为F(X˜)为有限集,则存在X0∈F(X˜)0使得X0≤Y.所以,X0≤Y≤X≤X˜,即X∈ [X0,X˜].因此,S(A,B,*)⊆[X0,X˜]⊆S(A,B,*).所以,S(A,B,*)=[X0,X˜].另一方面,由引理1.5及定理2.13知[X0,X˜]⊆S(A,B,*).所以,S(A,B,*)=[X0,X˜].
定理2.18 方程(1)有唯一解当且仅当F(˜X)={˜X}.
证明 ⇐ 由定理2.10与定理2.13可证得.
⇒ 由定理2.17可证得.
下面给出求解方程(1)极小解的步骤.
第1步:根据定理2.10计算˜X并检验˜X是否为方程(1)的解.如果不是,则 S(A,B,*)= Ø,结束;否则,转至第2步;
第2步:根据(19)式构造Ji(˜X),进一步,由(20)式构造J(˜X);
第3步:根据(22)式构造F(˜X);
第4步:根据定理2.16求出方程的极小解S0(A,B,*)=F(˜X)0;
第5 步:输出 S0(A,B,*).
例 2.3 考虑方程(1),其中


经计算,˜X=[0.3,1,0.2]T.经检验,˜X是方程的解,由(19)式得 J1= {2,3},J2= {1,2},则J(˜X)={(2,1),(2,2),(3,1),(3,2)}.
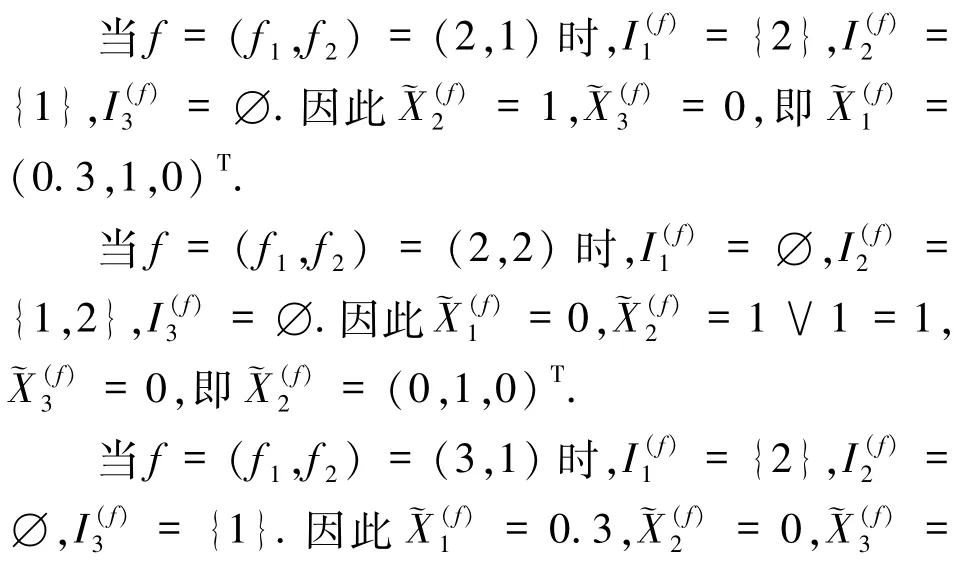
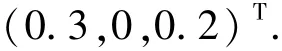
当f= (f1,f2)= (3,2)时{2},= {1}.因此0.2,即= (0,1,0.2)T.

*使用例2.1中的运算,则˜X=(0.8,0.75,0.5,0.6)T.经检验,˜X是方程的解,由(19)式得J1={1},J2={2,4},J3={3},J4={3},则J(˜X)={(1,2,3,3),(1,4,3,3)}.


