一种基于成对粒子的粒子群优化算法

汪在荣， 张文凤

（1.内江师范学院计算机科学学院，四川内江641110； 2.内江师范学院四川省数值仿真重点实验室，四川内江641110；3.重庆大学数学与统计学院，重庆401331）

函数最值求解问题是一个传统问题，对于函数最值求解的方法大致可以分为两大类.第一类是传统的数学分析方法，该类方法建立在数学分析和实变函数理论的基础上，通过分析函数性质求解，其解具有精确性等特征，然而对于较为复杂的函数，特别是无法显示表达以及可微性、连续性较差的函数，分析其数学特性往往十分复杂，使用分析法求解其最值的解是十分困难甚至无法进行的.第二种方法是在计算机技术高速发展的基础上建立的通过模拟计算求解最大值的方法，该方法抛开对于函数的特殊性质的要求，直接通过函数具体值的比较来寻找函数最大值.统计模拟方法求解函数最值可以解决传统分析方法无法解决的问题，但是求解过程计算量大，对于较为复杂的问题如果不进行算法的优化，即使大型计算机也难以得到要求精度的解，所以优化算法是现在最优值问题研究中的一个重要方向.

粒子群算法［1-15］是一种较为新颖的智能优化算法，1995年由文献［1］提出，最初是一种模拟鸟群和鱼群的群体智能算法，目标为搜索连续空间中的最优值.早期的粒子群算法存在着易发散、有趋同性等缺点，为了改进这些缺点，很多学者对粒子群算法进行了改进.文献［2-3］在每次速度迭代时为上一代速度乘以一个因子，称为惯性权重.由于动态惯性在复杂问题中容易使原算法陷入局部最优解中，又提出了模糊惯性权重法，以自适应地改变惯性权重.不过由于参数设定困难，所以尚缺乏大量使用.Clerc等［4］提出了压缩因子法来保证算法的收敛性，压缩因子本质上同惯性权重是等价的.同时，文献［5］从进化算法的角度出发，提出了结合进化算法的粒子群算法，如选择法、繁殖法等.同时从粒子通讯的角度，Zhao等［9］提出了基于粒子的空间位置划分的方案，有效地提高了PSO算法的性能.而文献［6］则测试了不同的邻域拓扑对于PSO算法的影响，发现根据不同问题有着不同的最优邻域拓扑模式.为了避免算法陷入早熟，文献［7-8］将混沌思想引入粒子群算法，将混沌空间映射到解空间，利用混沌系统的遍历性克服粒子群算法的早熟缺陷.从混合算法角度，许多学者尝试将粒子群算法与局部搜索算法结合，以改善粒子群算法的收敛速度和搜索精度.文献［9］尝试将算法分代，在每一代中重组粒子结构以搜索局部最优解.文献［10］则结合Nelder-Mead单纯形法对粒子群算法进行改进，通过Nelder-Mead方法计算局部最优.过去的算法确实能够提高粒子群算法的收敛速度与收敛精度，然而这些算法容易落入局部最优的陷阱.

本文给出一种基于成对粒子的混合粒子群算法，该算法通过调整拓扑结构改善粒子群算法的遍历性，同时通过构建和原粒子对应的具有随机梯度运动性质的成对粒子，在全局搜索的同时，较精确地搜索局部最优值，一方面加强了粒子群算法的全局收敛速度和精度，另一方面克服了粒子群算法容易陷入局部最优的缺陷，并以算例证明了该算法的优越性.

1 粒子群算法简介

1.1 粒子群算法原理与标准PSO 粒子群算法基本思想是在参数空间中随机播下一定量的点作为粒子，每个点根据函数取值由适应函数映射得到一个适应值，粒子在空间中根据自己和其他粒子的适应值按照一定方向运动.通过整个空间中粒子运动的迭代，求出空间中最优值.

最早提出的标准PSO算法，其数学表达如下：在一个n维搜索空间中，初始化m个粒子组成的点集｛x1，x2，…，xm｝，其中第 i个粒子的位置为（xi1，xi2，…，xin），其初始速度为0.计算出每个粒子的函数取值，设为向量p，并得到极值pg.根据p和pg以及第t代的速度通过迭代得到第t+1代粒子速度，并计算出粒子当前位置，其中

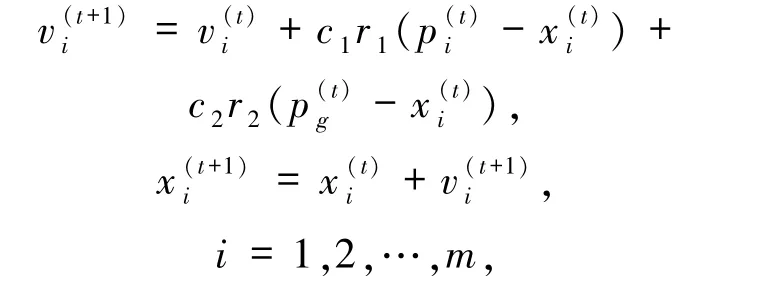
m 为种群规模，t为当代进化代数，r1、r2为［0，1］的实数，c1、c2为加速常数.为使速度不致过大，设置速度上限 Vmax，当｜v｜＞ Vmax时，令

1.2 改进粒子群算法PSON

1.2.1 惯性权重与收缩因子 为了加强对于PSO算法寻优轨迹的控制以优化PSO算法，在速度迭代式中加入一个惯性权重，即将速度迭代公式变为

此处的权重w（t）可以控制上一代速度对当前速度的影响，根据试验发现w（t）为动态时能够取得较好的寻优效果.一个常用的准则为线性递减权值，即

其中的参数常用取值为 wini＝0.9，wend＝0.4.

为保证PSO算法的收敛性，引入了收缩因子.设χ（·）为一个压缩算子，在不考虑惯性权重的基础上，迭代公式为

1.2.2 粒子通讯结构 上述的粒子群算法，每个粒子都与其他所有粒子建立通讯，并向自身最优值以及全局最优值加速，因而该方法存在易陷入局部最优解的问题，导致算法过早收敛，因此很多学者提出了局部粒子通讯方式与速度迭代公式.

对于第i个粒子，假设它只与周围的mi个粒子通讯为第i个粒子的第k个通讯邻居的第t步时的最优值位置表示粒子i自己在前t步时的最优位置，令

由（3）式可以看出，第i个粒子在第t+1步的速度取决于第t步时本身和其邻域内所有粒子的历史最优位置.该算法称为PSON算法.

1.2.3 粒子群算法的收敛性 本文采取的压缩因子粒子群算法中（w+1-φ）2-4w等价于（χ+1-χφ）2-4x，而本文中使用的参数 φ ＝ 4.2，χ＝，满足 Δ ＝ （χ+1- χφ）2-4χ＞0，故而本文使用的算法在全局通讯模式下是收敛的.

2 随机梯度粒子群算法

随机梯度搜索法能够有力地克服全局PSO算法易于过早陷入局部最优值的缺点，以及局部PSO局部收敛速度慢的缺点，在参数设置得当的情况，随机梯度搜索能够在局部收敛.同时，与粒子群算法内核易于结合，随机梯度算法可以看作单个粒子的一种随机搜索运动，而粒子群算法则是根据粒子间的通讯实现群智能来进行搜索，粒子群中的单个粒子没有搜索能力.如果将若干个这样运动的随机粒子加入群智能，赋予粒子群算法中的单个粒子搜索能力，则既可以防止粒子群算法的早熟，增强粒子群算法后期的收敛能力，又能有效利用群智能使搜索速度优于常规随机梯度算法.

2.1 PSON与随机梯度搜索的伴生粒子 PSON算法的本质是服从（3）式给出的速度迭代公式的粒子群算法，令

令其中加速权重ck与 k无关，均相等为 c，则 φk～ U［0，c］.

由（4）式不难发现，粒子对于自身最优值附近的局部最优的搜索较为缺乏，于是在此提出伴生粒子的概念.对初始化的粒子i，引入一个与之对应的伴生粒子i′，i′具有随机梯度粒子的行为模式，具体数学描述为：设伴生粒子i′的位置为，其中t*表示i′的迭代代数，产生一个随机的n维单位向量ζ（t*），则在方向 ζ（t*）上的梯度可以表示为

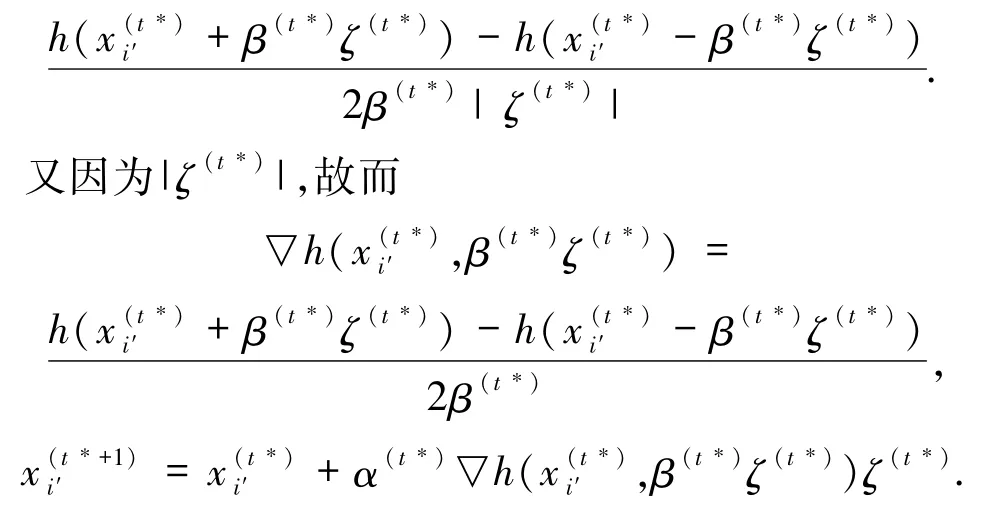
选择合适的参数序列α（t*）和β（t*），可以使伴生粒子在一个小区域内快速收敛到局部最优值.在粒子运动中，每次迭代均考虑粒子与伴生粒子的运动，粒子i在前t步的最优值取值为其本身与伴生粒子前t步的最优值中的较大值，最优位置为最优值的对应位置.

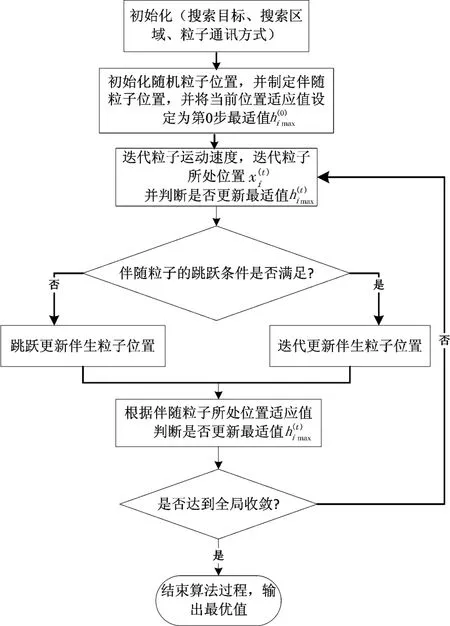
2.2 伴生粒子的跳跃条件 伴生粒子i′的目的是找出粒子i某个位置附近的局部最大值，故而当粒子i的随机化初始位置给定后，i′也在同一位置被初始化.之后随着粒子的不断运动，伴生粒子在一定情况下应当能够移动到粒子所在的新的位置进行搜索，并且重新初始化伴生粒子的相关参数.本文称伴生粒子的该行为为跳跃，并给出伴生粒子的跳跃条件.

设h为x的适应函数，它的值表示粒子在位置x的寻优表现，在一个求函数f最大值问题中，可以简单定义h≜f.

2）收敛跳跃.设伴生粒子i′在经过t*次迭代后，已经满足收敛条件在位置xi′附近收敛，而此时全局算法尚未收敛，则令伴生粒子跳跃至粒子i所处位置，即令，并初始化t*＝0，使伴生粒子在附近搜索局部最适值，以规避伴生粒子在某个局部收敛点进行无意义的迭代.

3）偶然跳跃.即使在1）和2）的条件都不满足的情况，也设伴生粒子i′有小概率p跳跃至粒子i的附近搜索粒子i的局部最适值，以增大搜索空间，避免整个算法落入一个局部最优陷阱.概率p可以是一个给定的参数，也可以是根据前t-1步最适值h（t-1）imax和粒子i在第t步适应值进行加权的参数，本文因为是对该算法的初探研究，主要研究概率p为一个定值的情况.

本文经过实验证明，使用常规跳跃策略容易使算法落入早熟陷阱，本文程序采用的是结合收敛跳跃和偶然跳跃两种策略原则的跳跃，同时经过实验发现，跳跃时伴生粒子i′直接跳跃至粒子i的策略并不是最优，而是跳跃至粒子i附近一个随机地点的策略较优.

在后续算例中，伴生粒子i′跳跃的随机性由一个正态分布给出，正态分布的方差由对应粒子i附近的粒子数加权，粒子i附近的粒子数越多，则说明粒子对该区域的搜索越密集，则伴生粒子跳跃随机项的方差越大，伴生粒子有更大的可能在相对远一些的区域进行搜索.

2.3 算法流程

3 算例分析与测试

3.1 Ackley函数的极大值 Ackley函数由图1所示，其最大值在（0，0）处取得.由图1易见该函数有很多局部最大值.

图1 Ackley函数图Fig.1 The image of Ackley function

使用随机梯度粒子群算法进行91次迭代，就找到了位于（0，0）的最优值，误差范围不超过1 ×10-17.

3.2 Rastrigin函数最小值搜索 为将最小值问题转化为最大值问题，将Rastrigin函数的函数值取相反数得到一个新的函数，在下文中为求简洁，在不引起混淆的情况下将新得的这个函数也称为Rastrigin函数，表达式为

其中n为x的维数，该函数的全局最大值在（0，0）处取得.

二维Rastrigin函数的图像如图2所示，已知其最大值在（0，0）处取得.Rastrigin由于具有非常多的局部最大值，所以对模拟退火算法等具有很强的欺诈性.随机梯度粒子群算法通过597次迭代求解出了Rastrigin函数的最大值点（0，0），误差不超过1 ×10-10.

3.3 Schaffer函数最大值搜索 Schaffer是一个检测搜索算法常用的函数：

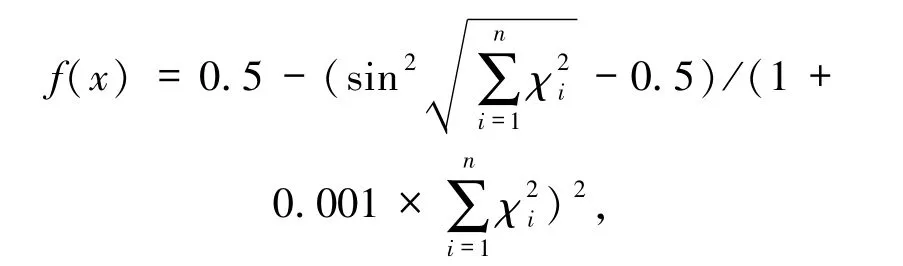
其中χ是一个向量.

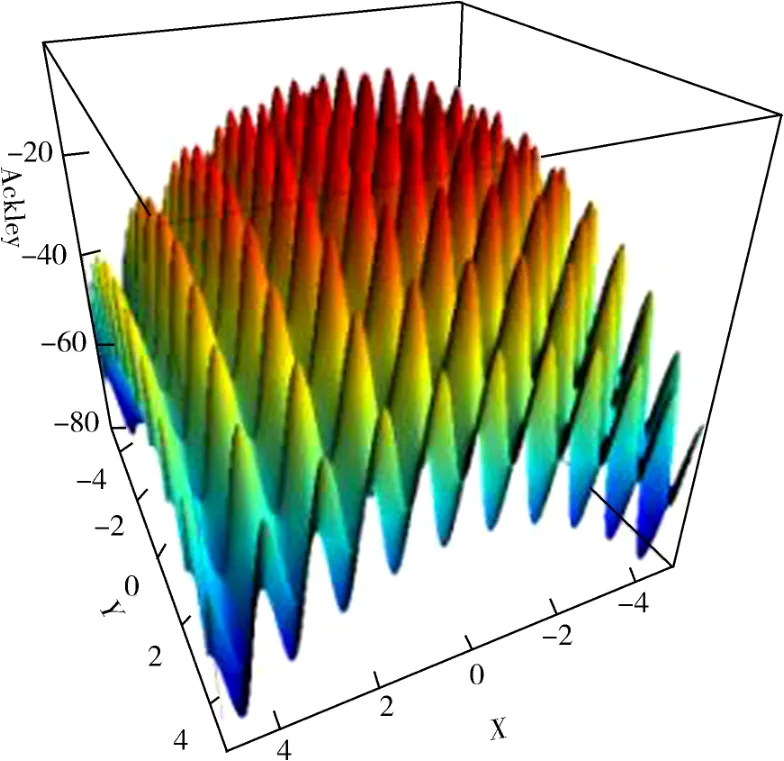
图2 二维Rastrigin函数图像Fig.2 The image of two-dimensional Rastrigin function

二维Schaffer函数图像如图3所示，其最大值在（0，0）处取得，最大值为1.而在其最大值外围一周的峰值上，局部最大值接近0.99，同时其最大值附近峰值区域较小，而局部最大值的环形区域较大，普通PSO和进化算法非常容易落入环形区域陷阱，得到一个局部最大值而错过全局最大值.使用本文提出的随机梯度粒子群算法通过978次迭代得到了正确的最大值，误差不超过1×10-9.

图3 二维Schaffer函数图像Fig.3 The image of two-dimensional Schaffer function

图4 为在搜索Schaffer函数最大值过程中，某个伴生粒子的运动轨迹.图4（a）为该伴生粒子运动的完全轨迹，为了更清晰地看出伴生粒子的运动轨迹与作用，图4（b）表示该伴生粒子最后200次运动的轨迹，图4（c）为该伴生粒子的运动趋势.

由图4可以看出，伴生粒子不容易陷于局部最大值处，观察图4（b）可以看到，当伴生粒子陷入环状极大值陷阱后，它能够跳出局部最大值在附近进行搜索，从而搜索到全局最大值.

图4 Schaffer函数搜索伴生粒子运动图像Fig.4 The motion image of associated particles searched by Schaffer function

3.4 Griewank函数最大值搜索 Griewank函数是一种连续的复杂函数，二维Griewank函数表达式为

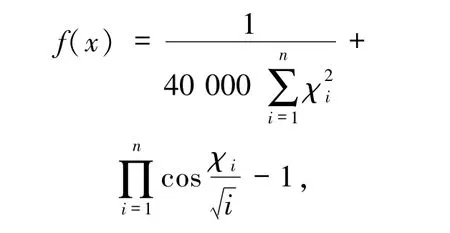
其中x是一个向量.

二维Griewank函数图像如图5所示，其最大值在（0，0）处取得.可以看出Griewank函数有多个局部最大值，一般搜索算法容易陷入局部最大值中.使用随机梯度粒子群算法在第577次迭代时已经收敛到（0，0）处的最大值，误差不超过1×10-9.

4 算法对比研究

本文通过重复模拟试验三维Schaffer函数试验，得到各算法性能（见表1），其中随机梯度粒子群算法模拟试验8次，27个粒子的PSON算法模拟试验12次，54个粒子的PSON算法模拟试验8次，PSO算法模拟试验10次，随机梯度算法模拟试验2 000次.各个算法的粒子初始位置均随机设置为｛（x，y，z）｜-10 ＜ x＜10，-10 ＜ y＜10，-10 ＜ z＜10｝，服从均匀分布的随机数.

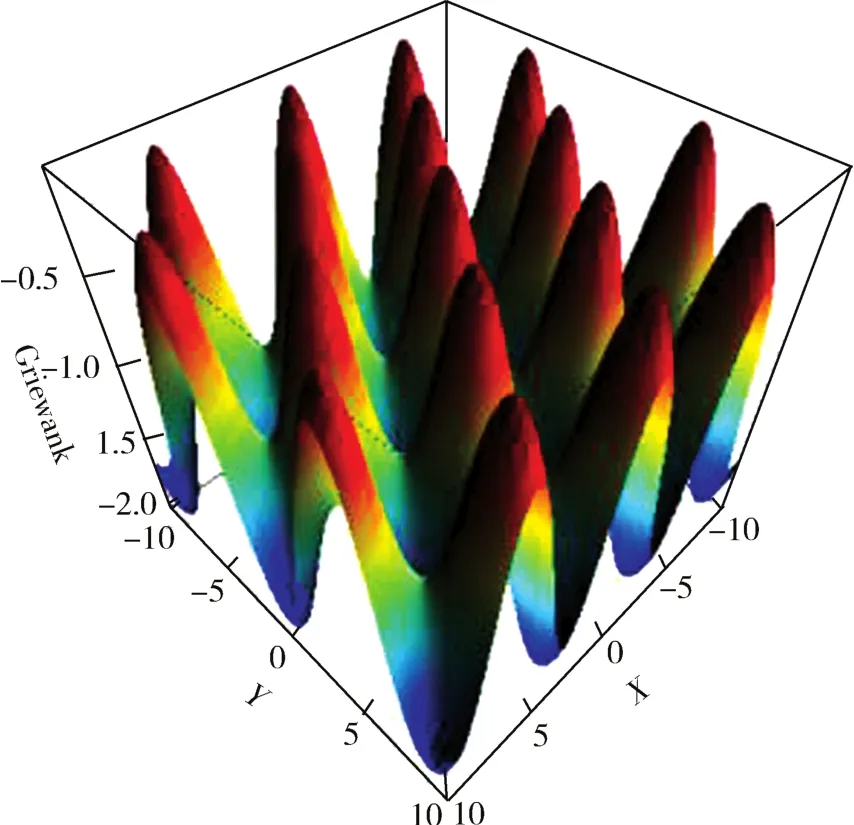
图5 二维Griewank函数图像Fig.5 The image of two-dimensional Griewank function

表1 三维Schaffer函数各算法搜索性能表Tab.1 Search performance tables for each algorithm of three dimensional Schaffer function

表1表明，随机梯度粒子群算法在各项性能上大幅优于PSON算法、标准PSO算法以及较为简单的随机梯度算法.对于复杂问题，单纯增加粒子群算法的粒子数并不能提升算法的寻优效果，反而会增加搜索时间成本，同时，对于一些复杂问题局部型PSO算法难以收敛，这不仅影响搜索的正确率，更会导致实践中整个系统问题处理的延误.如表1所示，如果加上算法未收敛时的时间进行平均，则其他算法的平均用时会大大超过随机梯度粒子群算法.

试验表明，随机梯度粒子群算法是一种效果良好的算法，有很好的应用前景.