数列知识结构与拓展

■河南省偃师高级中学 胡稳治

【数列知识结构】

【基础知识及拓展】

第一部分：数列的概念与简单表示法

(一)基础知识

1.数列的概念。

(1)按照一定顺序排成的一列数称为数列。按项数是否有限可分为有穷数列与无穷数列。

(2)数列可以看作以正整数集N*(或它的有限 子集 ｛1，2，…，n｝)为定义域的函数an=f(n)，当自变量按从小到大的顺序依次取值时所对应的一列函数值。

(3)数列作为特殊的函数，也有单调性。例如:递增数列，递减数列，常数列，摆动数列。

2.数列的表示法。

相对于函数的三种表示法，数列也有三种表示法:解析法，列表法，图像法。

(1)解析法。

①通项公式:如果数列的第n项与序号n之间的关系可以用一个式子来表示，那么这个公式叫作这个数列的通项公式。

②递推公式:由递推公式结合初始条件，可写出数列的各项或求出通项公式。

(2)列表法。

全体正偶数按从小到大的顺序构成的数列2，4，6，…，2n，…可用列表方法表示，如表1。

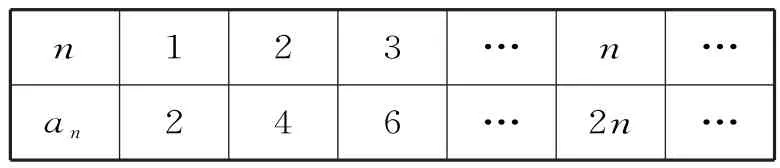
表1

(3)图像法。

数列的图像是一系列孤立的点。

(二)知识拓展

1.数列的单调性。

判断数列｛an｝的单调性，通常转化为判断｛an｝的相邻两项an，an+1的大小关系。

若an+1-an＞0，则数列｛an｝为递增数列;

若an+1-an＜0，则数列｛an｝为递减数列;

若an+1-an=0，则数列｛an｝为常数列。

若已知数列的单调性，则可求得该数列的最大项与最小项。

2.数列的周期性。

对于数列｛an｝，如果存在正整数T，对于任意的n∈N*，都有an+T=an，则称T为数列｛an｝的周期。

3.数列｛an｝的前n项和。

Sn=a1+a2+…+an，由此可知an=

第二部分：等差数列

(一)基础知识

1.等差数列的概念。

如果一个数列从第二项起，每一项与它的前一项的差等于同一个常数，那么这个数列就叫作等差数列，这个常数叫作等差数列的公差，公差通常用字母d表示。

2.等差数列的通项公式。

如果等差数列｛an｝的首项是a1，公差是d，则其通项公式为an=a1+(n-1)d。

3.等差数列的前n项和公式。

如果等差数列｛an｝的首项是a1，公差是

(二)知识拓展

1.等差数列的判定方法。

(1)定义法:对于数列｛an｝，若an+1-an=d(常数)，则数列｛an｝是等差数列。

(2)等差中项法:对于数列｛an｝，若2an+1=an+an+2，则数列｛an｝是等差数列。

2.等差数列的通项公式和前n项和。

已知等差数列｛an｝的首项是a1，公差是d。

(1)an=a1+(n-1)d=d n+(a1-d)，an是关于n的一次式。

(2)由an=a1+(n-1)d及am=a1+(m-1)d，两式相减得an-am=(n-m)d，

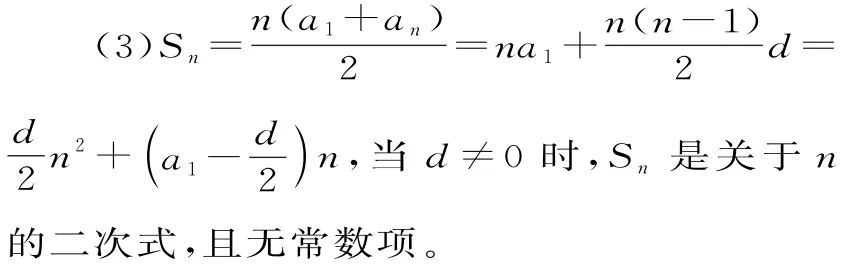
3.等差数列的性质。

(1)对于等差数列｛an｝，若m+n=p+q，则am+an=ap+aq，其中m，n，p，q∈N*。

特别地，若m+n=2p，则am+an=2ap，其中m，n，p∈N*。

(3)相隔等距离的项组成的数列仍是等差数列，即ak，ak+m，ak+2m，…仍是等差数列，公差为m d(k，m∈N*)。

(4)对于等差数列｛an｝，如果Sn是其前n项和，k∈N*，那么Sk，S2k-Sk，S3k-S2k成等差数列，公差为k2d(k∈N*)。

(5)等差数列｛an｝的单调性。当公差d＞0时，｛an｝为递增数列;当公差d＜0时，｛an｝为递减数列;当公差d=0时，｛an｝为常数列。

第三部分：等比数列

(一)基础知识

1.等比数列的概念。

如果一个数列从第二项起，每一项与它的前一项的比等于同一个常数，那么这个数列就叫作等比数列，这个常数叫作等比数列的公比，公比通常用字母q(q≠0)表示。

2.等比数列的通项公式。

如果等比数列｛an｝的首项是a1，公比是q，则其通项公式为an=a1qn-1。

3.等比数列的前n项和公式。

如果等比数列｛an｝的首项是a1，公比是q，则其前n项和公式为Sn=

(二)知识拓展

1.等比数列的判定方法。

(1)定义法:对于数列｛an｝，若q(q≠0)(常数)，则数列｛an｝是等比数列。

(2)等比中项法:对于数列｛an｝，若an·，则数列｛an｝是等比数列。

2.等比数列的通项公式和前n项和。

已知等比数列｛an｝的首项是a1，公比是q。

(2)由an=a1qn-1及am=a1qm-1，两式

3.等比数列的性质。

(1)对于等比数列｛an｝，若m+n=p+q，则am·an=ap·aq，其中m，n，p，q∈N*。

特别地，若m+n=2p，则am·an=a2p，其中m，n，p∈N*。

(2)若等比数列｛an｝的项数为2n，则若等比数列｛an｝的项数为2n+1，

(3)相隔等距离的项组成的数列仍是等比数列，即ak，ak+m，ak+2m，…仍是等比数列，公比为qm(k，m∈N*)。

(4)对于等比数列｛an｝，Sn是其前n项和，k∈N*，那么当q≠-1或q=-1且k为奇数时，Sk，S2k-Sk，S3k-S2k成等比数列;当q=-1且k为偶数时，Sk，S2k-Sk，S3k-S2k不成等比数列。

(5)Sm+n=Sn+qnSm=Sm+qmSn;若等比数列。

(6)等比数列的单调性。

①当q＞1，a1＞0或0＜q＜1，a1＜0时，｛an｝为递增数列;

②当q＞1，a1＜0或0＜q＜1，a1＞0时，｛an｝为递减数列;

③当q=1时，｛an｝为常数列;

④当q＜0时，｛an｝为摆动数列。

第四部分：数列的综合应用

1.数列求和。

(1)公式法:直接利用等差数列、等比数列的前n项和公式求和。

(2)分组求和法:若一个数列的通项公式是由若干个等差数列或等比数列或可求和的数列组成，则求和时可用分组求和法，分别求和后相加减。

(3)并项求和法:在一个数列的前n项中，可两两结合求解，则称之为并项求和。形如an=(-1)nf(n)的类型，可采用两项合并求解。

(4)倒序相加法:若一个数列｛an｝，与首末项等距的两项之和等于首末两项之和，求这个数列的前n项和可用倒序相加法。

(5)裂项相消法:若一个数列｛an｝的每一项都可以化为两项之差，并且前一项的减数恰与后一项的被减数相同，求和时中间项相互抵消，这种求和的方法就是裂项相消法。

(6)错位相减法:若{an}为等差数列，{bn}为等比数列，求数列{anbn}的前n项和，可由Sn-q Sn，求Sn，其中q为{bn}的公比。

2.求通项公式。

对于由初始条件和递推公式所确定的数列，通常可通过对递推公式的转化，构造等差数列或等比数列，通过求出等差数列或等比数列的通项公式，从而求出数列的通项公式。

(1)递推公式为an+1=f(n)an，通常做商f(n-1)可求，就可以使用累乘法求得an。

(2)递推公式为an+1=an+f(n)，通常做差变形为an+1-an=f(n)，只要f(1)+f(2)+…+f(n-1)可求，就可以使用累加法求得an。

(3)递推公式为an+1=p an+q(p，q为常数)，通常使用待定系数法构造新数列。

(4)递推公式为an-an+1=p an+1an(p