数列中易错点的归类剖析

■河南省洛阳市第一高级中学 王玮琪

一、忽视隐含条件致错

例1首项为-20的等差数列{an}，从第10项起各项均为正数，则其公差d的取值范围为 。

解析：由题意知，数列{an}满足

易错点分析：若不能准确把握等差数列的单调性，便不能认识到“前9项均为负数或0”这一隐含条件，从而忽视隐含着的“a9≤0”这一条件。实际上，等差数列要么是递增数列，要么是递减数列，要么是常数列。根据本题已知条件，数列{an}应是递增数列。

例2在等比数列{an}中，an·an+1=16n，则其公比为_____。

解析：因为an·an+1=16n，所以当n≥2时，an-1·an=16n-1，两式相除得q2=16。由条件知相邻两项同号，故q＞0，所以q=4。

易错点分析：本题易忽略隐含条件“q＞0”，导致得出“q=±4”这一错误结果。

二、an与Sn关系把握不准确致错

例3已知数列{an}的前n项和Sn=n2+2n+1，则其通项公式为 。

解析：当n≥2时，an=Sn-Sn-1=(n2+2n+1)-[(n-1)2+2(n-1)+1]=2n+1;

当n=1时，a1=S1=4。

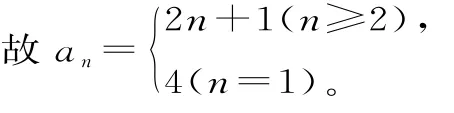
易错点分析：本题易将an与Sn的关系理解为an=Sn-Sn-1，从而得出an=2n+1，并且误认为{an}是等差数列。实际上，当公差d≠0时，等差数列的前n项和应为关于n

三、对等差数列前n项和的形式把握不准致错

易错点分析：本题易根据数列的前n项和的比，将{an}，{bn}的前n项和分别设为Sn=A(7n+45)，Tn=A(n+3)，从而造成结果错误。

四、求等差数列各项绝对值之和时出错

例5 在公差为d的等差数列{an}中，已知a1=10，且a1，2a2+2，5a3成等比数列。

(1)求d，an;

(2)若d＜0，求|a1|+|a2|+|a3|+…+|an|。

解析：(1)由题意得5a3·a1=(2a2+2)2，则d2-3d-4=0，解得d=-1或d=4。

所以an=-n+11，n∈N*或an=4n+6，n∈N*。

(2)设数列{an}的前n项和为Sn。因为d＜0，由(1)得d=-1，an=-n+11。

易错点分析：一是不注意按n≤11，n≥12分类讨论致错;二是在n≥12的情况下，求和时忽略前11项，而直接从第12项开始计算。

五、放缩法证明数列不等式时放缩不当

例6 设n∈N*，xn是曲线y=x2n+2+1在点(1，2)处的切线与x轴交点的横坐标。

(1)求数列{xn}的通项公式;

解析：(1)y'=(x2n+2+1)'=(2n+2)·x2n+1，曲线y=x2n+2+1在点(1，2)处的切线的斜率为2n+2，从而切线方程为y-2=(2n+2)(x-1)。令y=0，解得切线与x轴

综上可得，对任意的n∈N*，均有Tn≥

易错点分析：本题第(2)问是通过放缩的方法证明不等式的，由于不能直接求和，需要放缩后才能求和，并在求和后再进行放缩，放缩的尺度不恰当或放缩的起始项不恰当，是致错的主要原因。实际上，要证考虑通项，通过适当放缩能够使得每项相消即可。证明思路如下:先表示出Tn=当n≥2时，单独考虑