三角函数知识结构与拓展

■河南省偃师高级中学 周成玉

【知识网络】

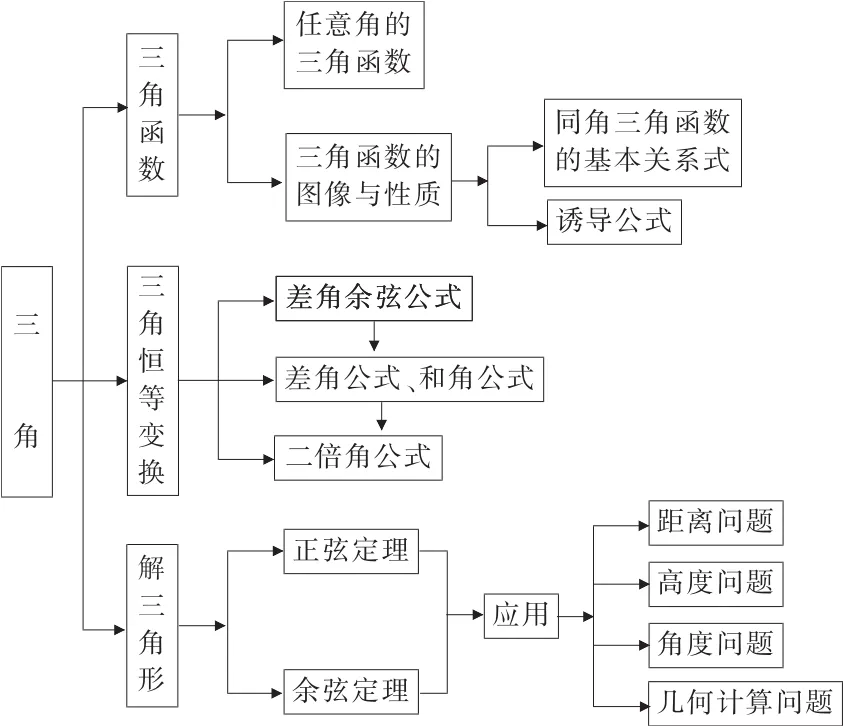
【基础知识及拓展】

第一部分：角的概念及任意角的三角函数

(一)基础知识

(1)角的概念;(2)终边相同的角的表示;(3)弧度制与角度制的互化(包括弧长公式和扇形面积公式);(4)任意角的三角函数的概念;(5)三角函数线。

(二)知识拓展

1.象限角与轴线角的表示。

(1)象限角。

(2)轴线角。

2.任意角三角函数的定义。

设P(x，y)是角a终边上异于顶点的任一点，其到原点O的距离为r，则sina=

3.三角函数值在各象限内的符号。

三角函数值在各象限内的符号口诀:一全正、二正弦、三正切、四余弦。

第二部分：同角三角函数的基本关系与诱导公式

(一)基础知识

(1)同角三角函数的基本关系式:sin2a+cos2a=1=tana;(2)诱导公式:要掌握2kπ+a(k∈Z)，-a，π+a，π-a，

(二)知识拓展

1.同角三角函数基本关系式的变形。

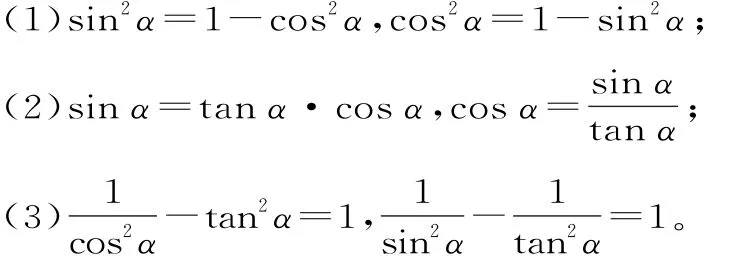
2.sina，cosa的齐次式的应用:分式中分子与分母是关于sina，cosa的齐次式，或含有sin2a，cos2a及sinacosa的式子求值时，可将所求式子的分母看作“1”，利用“sin2a+cos2a=1”代换后转化为正切求解。

3.掌握sina+cosa，sina-cosa，sinacosa的关系:(sina+cosa)2+(sinacosa)2=2。

4.应用诱导公式的重点是“函数名称”与“正负号”的正确判断。求任意角的三角函数值的问题，都可以通过诱导公式化为锐角三角函数的求值问题，具体步骤为:负角化正角→正角化锐角→求值。

第三部分：三角函数的图像和性质

1.正弦函数y=sinx，余弦函数y=cosx，正切函数y=tanx的图像与性质，如表1。

2.函数y=Asin(ω x+φ)的图像画法。

(1)五点作图法:找五个关键点，分别为使y取得最小值、最大值的点和曲线与x轴的交点。其步骤为:

(一)基础知识

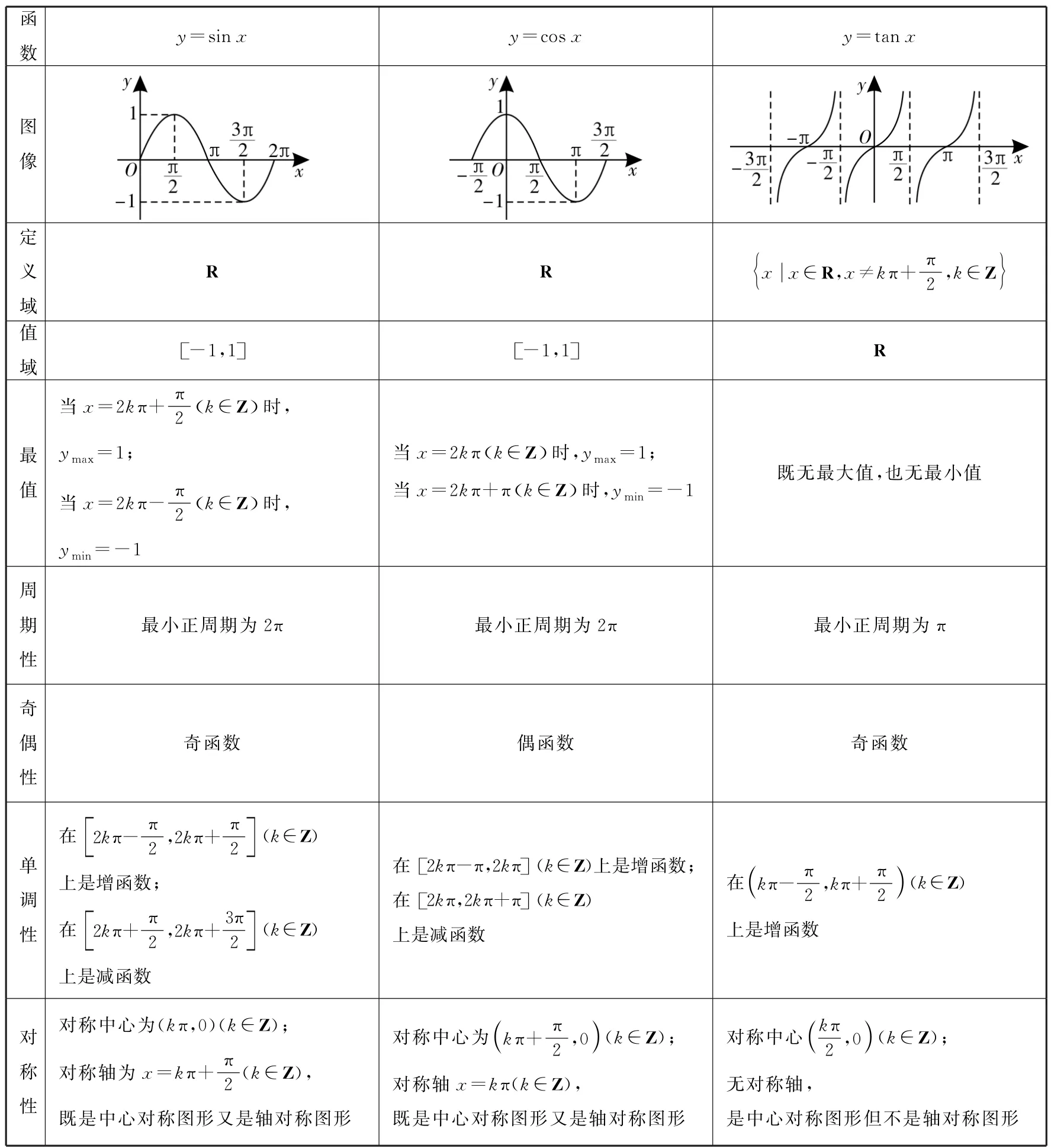
表1

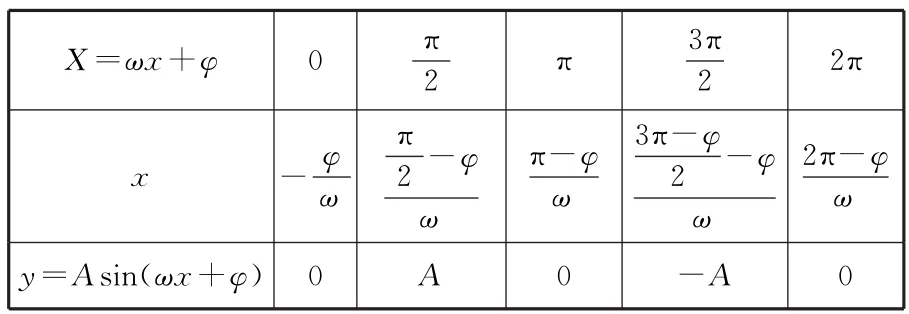
表2

由此可得五个关键点。

③描点画图，再利用函数的周期性把所得简图向左右分别扩展，从而得到y=Asin(ω x+φ)的简图。

(二)知识拓展

1.对于函数y=Asin(ω x+φ)的性质(定义域、值域、单调性、对称性、最值等)可以利用换元的方法，令X=ω x+φ，将其转化为研究y=sinX的性质。

2.函数y=Asin(ω x+φ)的对称轴由ω x+φ=kπ+，k∈Z确定，对称中心由ω x+φ=kπ，k∈Z确定其横坐标。

3.函数y=Acos(ω x+φ)的对称轴由ω x+φ=kπ，k∈Z确定，对称中心由ω x+φ=kπ+，k∈Z确定其横坐标。

4.f(x)=Asin(ω x+φ)(A≠0，ω≠0)为偶函数的充要条件是φ=+kπ(k∈Z);

f(x)=Asin(ω x+φ)(A≠0，ω≠0)为奇函数的充要条件是φ=kπ(k∈Z)。

g(x)=Acos(ω x+φ)(A≠0，ω≠0)为偶函数的充要条件是φ=kπ(k∈Z);

g(x)=Acos(ω x+φ)(A≠0，ω≠0)为奇函数的充要条件是φ=+kπ(k∈Z)。

5.求三角函数的最小正周期，一般先通过恒等变形化为y=Asin(ω x+φ)，y=Acos(ω x+φ)，y=Atan(ω x+φ)的形式，再分

6.求三角函数解析式的方法。

(3)求φ，常用方法有:

①代入法:把图像上的一个已知点代入(此时，A，ω，B已知)。

②五点法:确定φ值时，往往以寻找“五点法”中的第一个零点（，0）作为突破口，

具体如下:“第一点”(即图像上升时与x轴的交点中距原点最近的交点)为ω x+φ=0;“第二点”(即图像的“峰点”)为ω x+φ=;“第三点”(即图像下降时与x轴的交点)为ω x+φ=π;“第四点”(即图像的“谷点”)为ω x+φ=;“第五点”为ω x+φ=2π。

第四部分：三角恒等变换

(一)基础知识

1.两角和与差的正弦、余弦、正切公式。

2.二倍角的正弦、余弦、正切公式。

(二)知识拓展

1.公式的常用变形: (1)tana±tanβ=tan(a±β)(1∓tanatanβ)。(2)降幂公式:sinacosa=sin2a。(3)升幂公式:1+cos 2a=2cos2a;1-cos2a=2sin2a;1+sin 2a=(sina+cosa)2;1-sin2a=(sinacosa)2。(4)辅助角公式:asinx+bcosx=

2.三角化简、求值的常用方法:异名三角函数化为同名三角函数，异角化为同角，异次化为同次，切化弦，特殊值与特殊角的三角函数互化。

3.在化简时要注意角的取值范围。

4.给角求值中一般所给出的角都是非特殊角，从表面上来看是很难入手的，但仔细观察会发现非特殊角与特殊角之间总有一定的关系。解题时，要利用观察得到的关系，结合公式将非特殊角的三角函数转化为特殊角的三角函数，从而得解。

5.已知三角函数值，求其他三角函数式的值的一般思路:(1)先化简所求式子。(2)观察已知条件与所求式子之间的联系(从三角函数名及角入手)。(3)将已知条件代入所求式子，化简求值。

6.已知某种三角函数值来求角，在选取函数时，有以下原则:(1)已知正切函数值，则选正切函数。(2)已知正、余弦函数值，则选正弦或余弦函数。若角的范围是（0），则选正、余弦皆可;若角的范围是(0，π)，则选余弦较

第五部分：正弦定理和余弦定理

(一)基础知识

1.正弦定理和余弦定理，如表3。

表3

(二)知识拓展

1.三角形的内角和定理:在△ABC中，A+B+C=π，其变式为A+B=π-C，

3.在三角形中大角对大边，大角的正弦值也较大，正弦值较大的角也较大，余弦值则相反，即在△ABC中，A＞B⇔sinA＞sinB⇔cosA＜cosB。

4.在△ABC中，已知a，b和A，解三角形时，若求c，则也可以用余弦定理来解。

5.利用正弦、余弦定理判定三角形形状的两种思路:(1)“角化边”:利用正弦、余弦定理把已知条件转化为只含边的关系，通过因式分解、配方等得出边的相应关系，从而判断三角形的形状。(2)“边化角”:利用正弦、余弦定理把已知条件转化为只含内角的三角函数间的关系，通过三角恒等变换，得出内角间的关系，从而判断出三角形的形状，此时要注意应用A+B+C=π这个结论。

6.求三角形面积的方法:(1)若三角形中已知一个角(或该角的正、余弦值)，结合题意求所夹这个角的两边或该两边之积，代入公式求解。(2)若已知三角形的三边，可先求其一个角的余弦值，再求其正弦值，代入公式求面积。

7.三角形中，已知面积求边、角的方法:三角形面积公式中含有两边及其夹角，故根据题目的特点，若求角，就寻求所夹这个角的两边的关系，利用面积公式列方程求解;若求边，就寻求与该边(或两边)有关的角，利用面积公式列方程求解。

8.求最值或范围时，注意公式的选择。

(1)求取值范围时，用正弦定理转化为解三角函数的值域问题。

(2)求最大或最小值时，用余弦定理和均值不等式。注意均值不等式只能求一端的最值，有时也可由两边之和大于第三边求另一个。