车辆半主动悬架分数阶天棚阻尼控制器设计
李 健,杨 建,柴 星,闻登沈 ,刘遵港,王春波,张德龙
(1.营口忠旺铝业有限公司,辽宁 营口 115000; 2.中国重型机械研究院股份公司,陕西 西安 710032)
0 引 言
近年来,半主动空气弹簧悬架研究与应用受到国内外汽车界的广泛关注。半主动空气悬架可以根据路面情况及需求自适应调节刚度或阻尼系数,其控制简单、性能可靠,对车辆行驶平顺性和操纵稳定性有重要影响,在大客车、载重卡车以及工程车辆上广泛采用,特别是在多轴载重汽车领域应用更加普遍。国内外学者对半主动控制悬架开展了大量研究[1-6],所研究的控制算法包括天棚/地棚阻尼控制、模糊PID控制及滑模控制等,但大多都是基于整数阶的控制建模方法。
分数阶微积分,指微分、积分阶次可以是任意的或者说是分数的,它扩展了大家所熟知的整数阶微积分描述能力。在很多方面应用分数阶微积分数学模型,可以更准确地描述实际系统的动态响应[5]。分数阶控制器就是用分数微分方程来描述的控制器,并越来越受到研究者们关注,文献[6]通过最小化积分平方误差给出了一种分数阶控制器,文献[7]给出了一些分数阶控制器的数值例子,文献[8]设计了一个PIα控制器,文献[9]针对二惯性系统的速度控制提出了一个分数阶的PIαD 控制器。诸多研究表明,分数阶控制器比整数阶控制器具有更优的控制性能。
同时,考虑到空气弹簧系统的实际工作情况要更为复杂,不仅与本身结构参数有关,还受到气囊温度、压力及气体可压缩特性的影响。另外,由于分数阶PID控制器已有较多研究,其设计参数较多,实现较为困难。对于各种实际系统,分数阶模型比整数阶模型准确,也为一些动态过程描述提供了很好的工具,针对这些分数阶系统,分数阶控制器能更好体现它的优点。
为此,以某载重汽车空气悬架为研究对象,引入分数阶微积分理论对运动微分方程中的控制力项进行修正,建立半主动空气悬架分数阶天棚阻尼控制器模型,探讨并分析微分算子α及阻尼力系数c对控制指标的影响规律。
1 半主动空气悬架的1/4车辆模型
装有半主动空气悬架的1/4车辆模型如图1所示,车辆及空气悬架相关参数见表1。

图1 自由度的1/4车辆模型

表1 车辆参数

根据图1所示1/4车辆模型的悬架模型,建立其动力学方程为:
(1)
式中:Fd为可变阻尼力,其表达式可写为:
(2)
式中:csky为天棚阻尼系数。
2 分数阶天棚阻尼控制器设计
2.1 分数阶微积分基本理论

(3)
在实际工程应用中,最常用的分数阶微积分定义是Riemann-Liouville(RL)定义、Grünwald-Letnikov(GL)定义以及Caputo分数阶微积分定义[11]。
RL定义为:
(4)
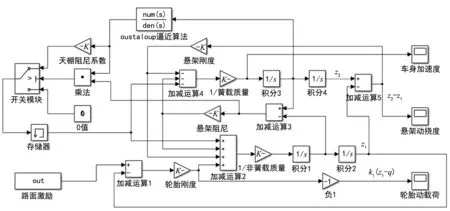
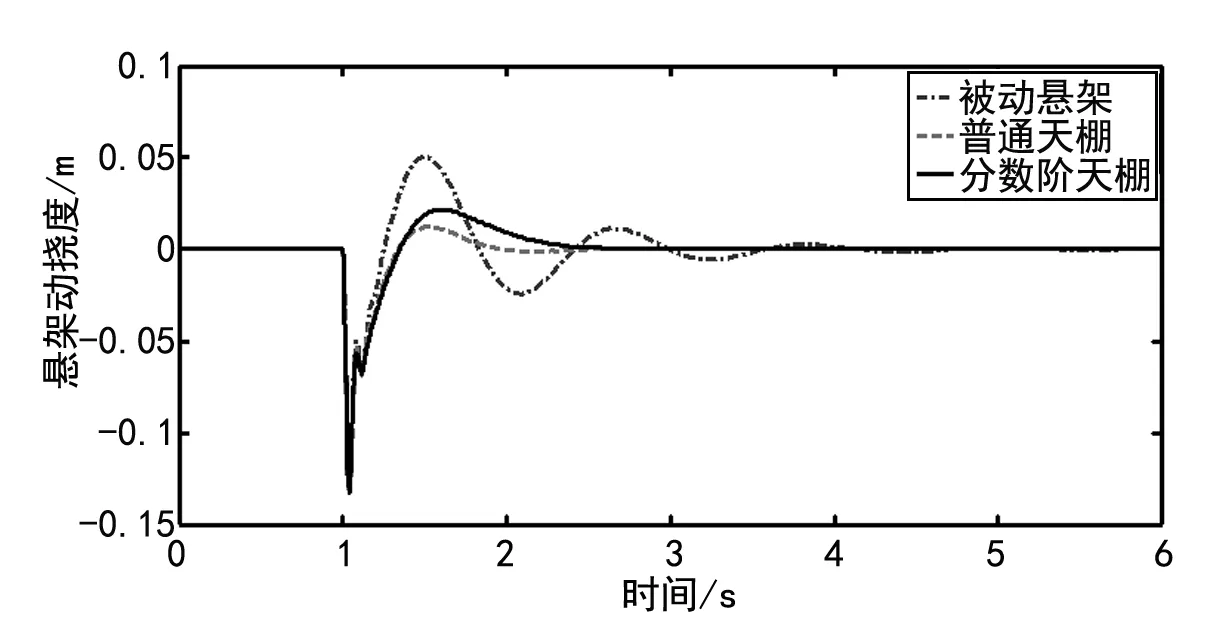
式中:m-1<α GL定义为: (5) Caputo微分定义为: (6) 式中:n-1<α 对于分数阶微积分方程,如果在t=0时刻有输入与输出信号u(t)和y(t),则传递函数为: (7) 天棚阻尼控制由美国的Karnopp教授在1974年首次提出[13],并在悬架半主动控制系统中得到广泛应用。天棚阻尼控制根据它是否可以在实际车辆悬架中采用,分为理想天棚和实际天棚阻尼控制。笔者研究的实际整数阶天棚阻尼控制力与其簧载质量速度成正比,即: (8) 式中:Fd为天棚阻尼力;csky为天棚阻尼系数。 考虑到空气弹簧所用材料的记忆性和粘弹性,在原有的普通天棚阻尼控制策略中引入了分数阶微积分的思想,用对悬架车身位移的分数阶导数来代替原来的车身速度,得控制力表达式为: (9) 式中:Dα表示为分数阶微分算子;c为天棚阻尼系数。 控制策略为: (10) 分数阶天棚阻尼系数c和微分阶次α均可优化,而整数阶天棚阻尼只有csky可调,在Matlab/Simulink中建立半主动空气悬架的分数阶天棚阻尼控制器模型如图2所示。 图2 分数阶天棚阻尼控制器模型 对图2所示的分数阶天棚阻尼控制器进行求解时,采用Oustaloup逼近算法来仿真分数阶微积分[14-15],其原理是用高阶的传递函数近似替代分数阶算子Dα。假设选定的拟合频段为(ωb,ωh),针对分数阶微积分算子Dα用信号滤波器进行拟合,构造出连续滤波器的传递函数模型为: (11) 式中:ωk′、ωk和K分别为: 式中:2N+1为滤波器的阶次。具体求解算法如下: (1) 给定近似频率段的范围和滤波器的阶次; (2) 根据分数阶微积分的阶次α,分别由上式计算ωk′、ωk和K; (3) 计算出近似化的有理传递函数。 注:对于近似频率的上下限ωb和ωh,由于算法本身特点,应选取ωbωh=1。 分数阶控制的参数通过最优算法来确定。为了提高汽车行驶平顺性和操纵稳定性,应尽可能减小簧载质量垂向加速度(车身加速度)、轮胎动载荷、悬架动挠度等指标。由于车身加速度、轮胎动载荷和悬架动挠度三个指标本身是冲突的,如何确定最优控制参数,能够使这三个指标达到最佳平衡点是一个优化问题。为此,通过选取合适的控制参数,建立一个综合性能目标函数J,如式(12)所示,使悬架综合性能达到最佳。 (12) 式中:q1为车身加速度加权系数;q2为悬架动挠度加权系数;q3为轮胎动载荷加权系数,参照文献[16]取q1:q2:q3=1:3000:8000。 在仿真计算中,采用的路面激励为B级路面,车速为20 m/s的高斯白噪声模型。通过计算,得出整数阶/分数阶天棚阻尼控制的综合性能目标函数与控制参数的关系如图3和图4所示。 图3 整数阶天棚阻尼控制 图4 分数阶天棚阻尼控制 由上图可以得出,当csky=1 894.4 Ns/m时,整数阶天棚阻尼控制策略的综合性能指标最小,为13.97;当c=1 650 Ns/m,α=0.32时,分数阶天棚阻尼控制下的综合性能指标最小,为12.21。可以看出在最优控制参数下,分数阶天棚阻尼控制下的综合性能指标要小于整数阶天棚阻尼控制,进一步验证了分数阶天棚阻尼控制要优于整数阶天棚阻尼控制。 基于Matlab/Simulink分别建立整数阶/分数阶天棚阻尼控制器模型,限于篇幅,略去整数阶天棚阻尼控制器模型,分数阶天棚阻尼控制模型如图2所示。将上节确定的最优控制参数输入到控制器模型中进行仿真,可得图5~7所示的仿真结果。表2为1/4车辆在整数阶和分数阶天棚控制策略下车身加速度、轮胎动载荷和悬架动挠度均方根值对比结果。 图5 车身加速度响应曲线 三项指标中,车身加速度影响着汽车的行驶平顺性,轮胎动载荷则影响着汽车的行驶安全性。通过上述结果可以看出,在车身加速度和轮胎动载荷指标上,分数阶天棚阻尼控制都是最优的,整数阶天棚控制次之,被动控制最差;在悬架动挠度上,整数阶天棚控制最优,分数阶天棚控制次之,被动控制最差。总体来说,分数阶天棚控制是优于整数阶天棚控制的。 表2 三项指标均方根值比较 图6 悬架动挠度响应曲线 图7 轮胎动载荷响应曲线 为进一步分析和观察整数阶/分数阶天棚阻尼控制器在阶跃输入激励下各响应量对比结果,取振幅为+0.1 m阶跃激励,得到车身加速度、悬架动挠度和轮胎动载荷的仿真结果如图8~10所示。 图8 阶跃激励下的车身加速度响应 从图中可以看出,在车身加速度和轮胎动载荷指标衰减过程中,分数阶天棚阻尼控制优于整数阶天棚阻尼控制,而被动悬架最差;在悬架动挠度指标衰减过程中,整数阶天棚阻尼控制略优于分数阶天棚阻尼控制,被动悬架最差。 图9 阶跃激励下的悬架动挠度响应 图10 阶跃激励下的轮胎动载荷响应 (1) 建立了2自由度的1/4车辆半主动控制悬架动力学模型,引入分数阶微积分理论,推导得到该空气悬架的控制方程。基于此构建了分数阶天棚阻尼控制器模型,利用Oustaloup算法对分数阶非线性微分方程进行数值求解,得到车身加速度、悬架动挠度和轮胎动载荷的响应值。 (2) 利用Matlab/Simulink建立1/4车辆仿真模型,对比分析整数阶/分数阶天棚阻尼控制效果,得到最优控制参数。后者能更有效抑制车身加速度和轮胎动载荷,衰减车身共振,提高车辆的平顺性和安全性,验证了分数阶微积分在悬架半主动控制中的有效性。 (3) 在悬架动挠度指标上,整数阶和分数阶天棚阻尼控制比较接近,前者略微优于后者。从综合性能指标来看,分数阶天棚阻尼控制优于整数阶天棚阻尼控制。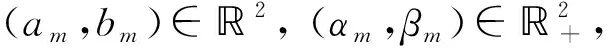
2.2 分数阶天棚阻尼控制器
3 仿真控制研究
3.1 最优控制参数的确定


3.2 仿真结果分析






4 结 语

