基于十字连通形环形谐振腔金属-介质-金属波导的折射率传感器和滤波器∗

祁云平 张雪伟 周培阳 胡兵兵 王向贤

1)(西北师范大学,物理与电子工程学院,甘肃省智能信息技术与应用工程研究中心,兰州 730070)

2)(兰州理工大学理学院,兰州 730050)

(2018年4月20日收到；2018年7月19日收到修改稿)

1 引 言

对于集成光学元件和高速电子器件,为了获得大带宽和快速处理系统,这两种结构的尺寸必须一致,但光子器件要比电子器件大得多.因此,必须采用特殊的技术制造光子器件,主要面对的挑战是克服亚波长光学结构的衍射极限[1].表面等离极化激元(surface plasmon polaritons,SPPs)是一种沿着金属与介质界面传播的倏逝波,在垂直界面方向上,振幅以指数形式衰减,故SPPs只在金属和介质界面的狭小范围内传播,SPPs具有很好的限域特性.因此,SPPs可以突破传统光学中的衍射极限,从而应用亚波长结构的约束特点来引导光场,实现亚波长光学器件的集成[2−4].近年来,在亚波长尺度下基于SPPs的波导结构被广泛研究,主要以介质-金属-介质(insulator-metal-insulator,IMI)波导和金属-介质-金属(metal-insulator-metal,MIM)波导为主,其中MIM波导具有更小的模式尺寸[5−7].目前,具有各种功能的基于SPPs的MIM波导光学元件,比如:Y-形合成器[8]、分路器[9]、马赫-曾德尔干涉仪[10]、滤波器和传感器[11,12],在理论研究与实验中都取得了验证与重大突破.

亚波长光学器件中,折射率传感器是重要的光学元件.在过去的几年中,基于表面等离子体共振(surface plasmon resonance,SPR)的传感器已经得到了广泛的研究,尤其是折射率传感和SPR生物传感[13−17].由于SPPs和局域表面等离子体共振(localized surface plasmon resonances,LSPR)对周围环境和结构的介电性能的高度敏感性[18,19],SPPs和LSPR在传感应用中表现出非常重要的特性.灵敏度(sensitivity,S)是表征传感器性能的一个关键参数,提高灵敏度可以提高检测的极限范围.目前,对于折射率传感器的研究中,Zhang等[20]报道了一种复合矩形亚波长孔阵列折射率传感器,其灵敏度为178 nm/RIU；Huang等[21]报道了高角度折射率传感器灵敏度超过500◦/RIU；2017年,Tang等[12]设计了基于Fano共振的MIM波导耦合谐振腔的折射率传感器,灵敏度高达1125 nm/RIU.然而,与光纤传感器相比[22,23],等离子体传感器有其优点:体积小,易于集成,但灵敏度不如光纤传感器高.Wu等[23]报道了光子晶体光纤折射率传感器,灵敏度高达30100 nm/RIU.因此,如何提高灵敏度是设计等离子体折射率传感器中的一个关键问题.与此同时,对于光子器件的研究中,滤波器也在微纳光子学器件中扮演着重要角色.研究者设计了多种滤波器,如齿形波导滤波器[24]、分叉型波导滤波器[8,25],此类型滤波器是由相位差决定通阻特性.这些滤波器的特点是允许大多数波长范围的光通过该结构,同时禁止一个或几个波长,被称为带阻滤波器或陷波滤波器.然而,基于谐振器的共振耦合特性来产生多种共振模式实现带通滤波器的设计同样具有重要意义[26−28].

基于以上思路,本文设计了一种两个MIM波导通过连通形环形谐振腔耦合的折射率传感器.相比于以往报道[12,20,21]的等离子体折射率传感器,灵敏度高达1500 nm/RIU.通过有限元方法(finite element method,FEM)研究了SPPs传输特性,分析了三种共振模式下透射峰与介质折射率的关系、共振峰波长与环形谐振腔中心半径的关系以及结构参数变化对传输特性的影响.此外,该结构除了传感器的应用之外,由于其在多种模式共振波长下的高透射率,在较大波长范围内实现共振波长的可调谐,该器件还可以用作带通滤波器.本文理论上也研究了环腔的特征波长与有效折射率,这与FEM数值研究结果符合得很好.研究结果将对可调谐滤波器、频谱分析仪和传感器等方面的应用具有重要意义.

2 模型建立与理论分析

MIM波导可以传播传统电介质波导所不具有的SPPs模式,这种SPPs模式没有截止宽度,狭缝宽度远小于波长时仍然可以传播,其有效折射率取决于金属和电介质的介电常数以及狭缝尺寸.由于SPPs的偏振选择性,MIM波导内的SPPs模式只能由TM偏振光激发,TE偏振光无法激发.具体而言,TM偏振光入射时,由Maxwell方程组和边界条件,可以解得MIM波导中的本征模式,其中TM0模式为对称模式.如图1所示,MIM波导中在横向磁场的基模(TM0mode)传输的色散关系[24,26]为

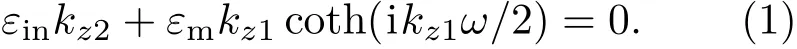
由动量守恒定义kz1和kz2的关系式为

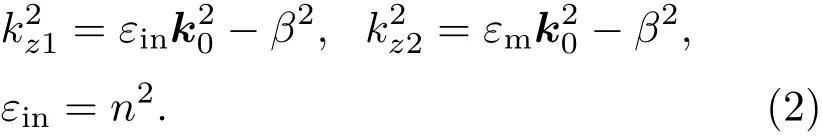
(2)式中,εin为介质的介电常数；β为传播常数；k0为自由空间中波矢,k0=2π/λ0.

图1中插图为MIM波导结构示意图,灰色区域和白色区域分别为金属材料和填充介质.填充介质的折射率为n,金属材料为银,银的相对介电常数采用Drude模型[26]:

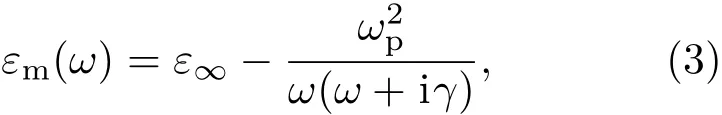
(3)式中ω为入射光的角频率,无穷介电常数ε∞=3.7,等离子体振荡频率ωp=9.1 eV,阻尼系数γ=0.018 eV.

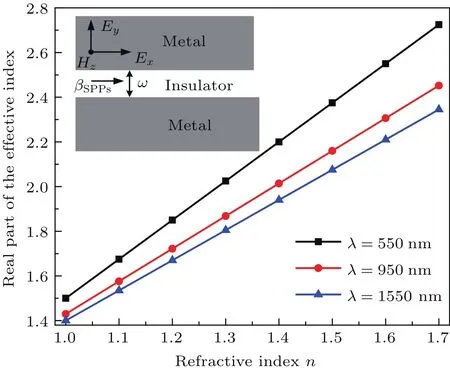
图1 MIM波导结构在不同入射波长下,有效折射率实部与介质折射率n色散关系[26]Fig.1. Real part of the effective index nfiversus the refractive index n of the insulator in a slit MIM waveguide structurefor different incident wavelengths of λ=550,950 and 1550 nm[26].

在波导中传播的横向磁场TM0模式的电磁波满足方程[28]:

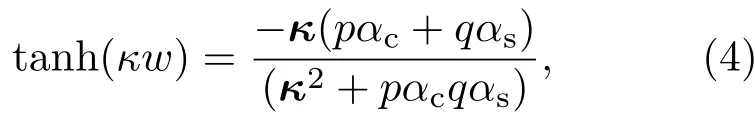
(4)式中κ和w分别为波导中传播的电磁波波矢和波导宽度.由于相同的金属银膜组成的MIM波导,则有p=q和αc= αs. 其中(4)式中p= εin/εm,αc=[k20(εin− εm)+ κ]1/2, εin和εm分别为介质和金属的介电常数.用迭代法[28]求解(4)式中的波矢κ,则有效折射率nfi=real(β/k0)=(εm+(κ/k0)2)1/2. 由此可得波导中SPPs的传播波长λSPPs= λ0/Re(nfi),Re(nfi)为有效折射率的实部.在图1中狭缝宽度w=50 nm,介质折射率n以0.1步长由1到1.7变化.金属材料采用银膜.由图1色散曲线可以很明显地看出,在特定波长下介质有效折射率与折射率n呈线性关系.

本文提出的环形谐振腔MIM波导二维结构示意图如图2所示,它由两个一端封闭的MIM波导和一个连通的环形谐振腔组成.两端MIM波导通过环形腔耦合.环形腔通过狭缝连通,狭缝宽度均为w.为了使波导中只有横向磁场的基模(TM0mode)传播,波导与环形腔的宽度w均固定为50 nm[27,28].金属材料为银,其中银材料的参数根据实验结果文献[29,30]中的数据由三次样条插值法计算得到,具体的银材料参数参见附件1的说明和数据.左右两侧波导与环形谐振腔的间距为d.其中,环形腔的内环半径为R1,外环半径为R2,我们定义环中心半径R=(R1+R2)/2.根据环形谐振腔理论[27]的谐振条件,可以用下面的公式从理论上得到环形谐振腔的谐振波长:

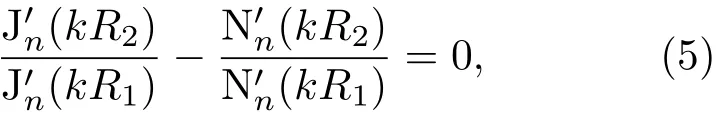
(5)式中k=ω(ε0εrµ0)1/2；µ0为空气中磁导率；εr为色散介质等效相对介电常数,εr=(nfi)2/µ0；Jn和Nn分别为n阶第一类贝塞尔函数和n阶第二类贝塞尔函数；为贝塞尔函数对宗量参数(kR)的导数.我们采用有限元法数值研究环形谐振腔MIM波导SPPs的传输特性.数值模拟时,采用散射边界条件,在TM0模式下SPPs从左侧端口被激发,通过与环形谐振腔耦合,只有在特定波长满足共振条件才能有效传输到右侧波导.用透射率T描述环形谐振腔MIM波导的SPPs传输特性,T=Pout/Pin,其中,

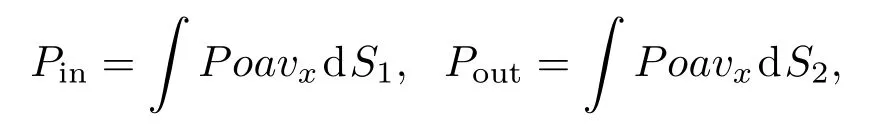
Pin为入射端口的入射功率,Pout为出射端口的出射功率,Poavx为时间平均功率流的x方向分量.

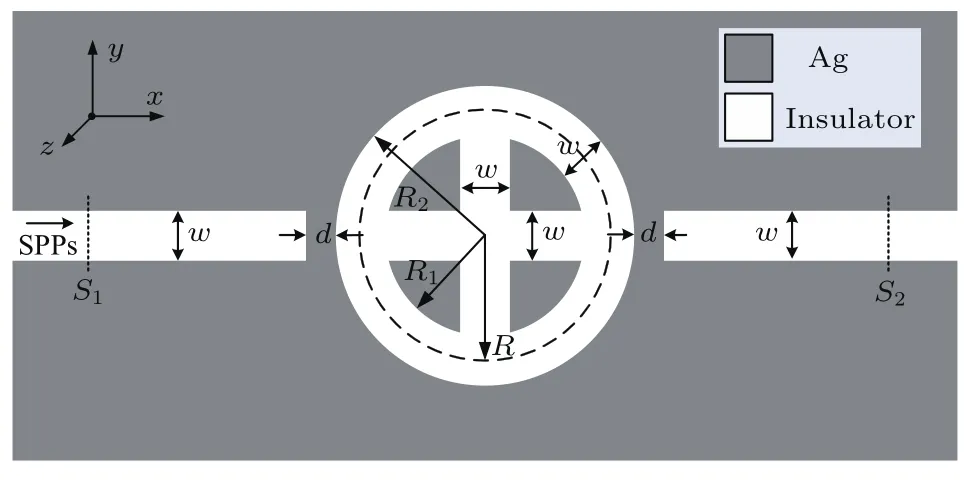
图2 环形谐振腔MIM波导结构示意图Fig.2.2D Structure schematic of two slits MIM SPPs waveguides with a ring resonator.

3 结果与讨论

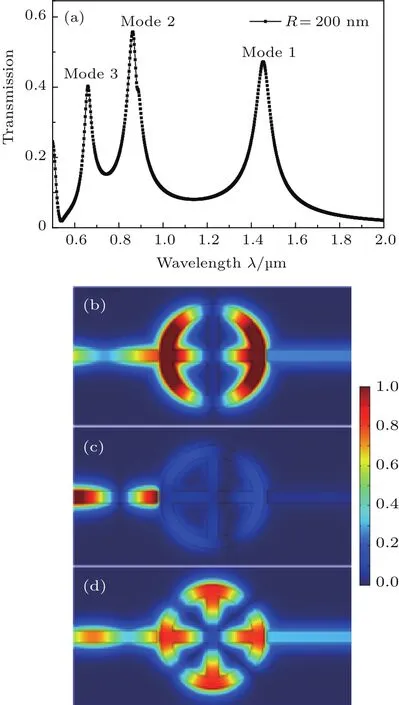
图3 (a)连通形环形谐振腔MIM波导透射谱；不同波长下连通形环形谐振腔磁场Hz分布(b)λ=1454 nm,(c)λ=1140 nm,(d)λ=862 nmFig.3.(a)The transmission spectrum of MIM SPPs waveguides with a ring resonator.The contour profiles of field of Hzof the nanoscale ring resonator at different wavelengths of(b)λ=1454 nm,(c)λ=1140 nm,(d)λ=862 nm.Here,R=200 nm,w=50 nm,d=10 nm,and n=1.

图3(a)给出了圆环谐振腔中心半径R=200 nm,w=50 nm,介质为空气n=1,波导与环形谐振腔的间距为d=10 nm时的透射谱.由图3(a)看出有三个明显的透射峰,相对应的峰值波长分别为λ=1454 nm,λ=862 nm,λ=660 nm.为了研究谐振腔内的共振模式,我们计算了在不同入射波长(λ=1454,1140,862 nm)入射时磁场Hz分量的稳态分布,如图3(b)—(d)所示.其中,图3(b)和图3(d)的稳态磁场分布图分别对应于图3(a)的透射峰Mode 1和Mode 2,可以看出在这两种模式下在环形腔及狭缝中形成驻波共振且有很强的磁场分布.因此,SPPs能通过环形谐振腔传输到右侧波导,从而形成透射峰.图3(c)为入射波长λ=1140 nm时磁场分布图,当入射波长λ=1140 nm为透射最低点.由图3(c)可以看出,其磁场分布与图3(b)和图3(d)明显不同,其磁场在环形谐振腔中的分布较弱,且在右侧波导中达到了SPPs禁止传输.

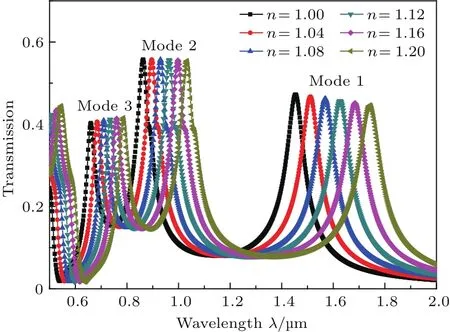
图4 改变介质折射率n时的透射谱Fig.4.The transmission spectrum of the structurefor different n.

为了研究介质折射率n对环形谐振腔MIM波导传输特性影响,我们计算了不同折射率n时的透射光谱,其中R=200 nm,w=50 nm,d=10 nm.图4给出了介质折射率n以步长0.04 RIU由1增加到1.2时的透射光谱.由图4可以看出,随着折射率的增大,透射光谱发生红移,且在Mode 1下的透射峰红移量最大且峰值略微减小.为了更直观地描述由折射率变化引起的传感特性变化,图5(a)给出了三种透射峰模式下共振波长与折射率n的关系,其中,实点为仿真值,直线为理论计算结果拟合曲线.由图5(a)可以明显看出,三种模式下透射峰对应波长与折射率n呈线性关系.随着折射率n增大,三个峰值波长均线性增大.图5(b)给出了三种模式下共振峰波长偏移量δλ随折射率增加量δn的关系,其中折射率增加量为0.04 RIU,RIU为折射率单位.当折射率由1增加到1.2时,Mode 1对应透射峰波长增加了300 nm,Mode 2对应透射峰波长增加了170 nm,Mode 3对应透射峰波长增加了124 nm,对于折射率传感器灵敏度,S=δλ/δn.则可以得到三种模式对应折射率传感器灵敏度分别为:1500,850,620 nm/RIU.相比2014年Wu等[26]报道的基于环形谐振腔结构的等离子体波导传感特性中Mode 1,Mode 2和Mode 3的三种模式下折射率传感灵敏度分别为:1476.25,732.92,483.75 nm/RIU.在结构几何参数相近的情况下,我们给出的结构的折射率传感灵敏度都有所提高.根据检测分辨率的定义:折射率增加量δn与折射率传感器灵敏度S的比值δn/S=(δn)2/δλ.可得相应的检测分辨率分别为:1.33×10−4,2.35×10−4,3.24×10−4RIU.根据图5(a)和图5(b)透射光谱的峰值与折射率之间的线性关系,在检测到的透射光谱的峰值波长时,可以获得被测材料的折射率.因此,本文提出的结构对于折射率传感器具有一定现实指导意义.

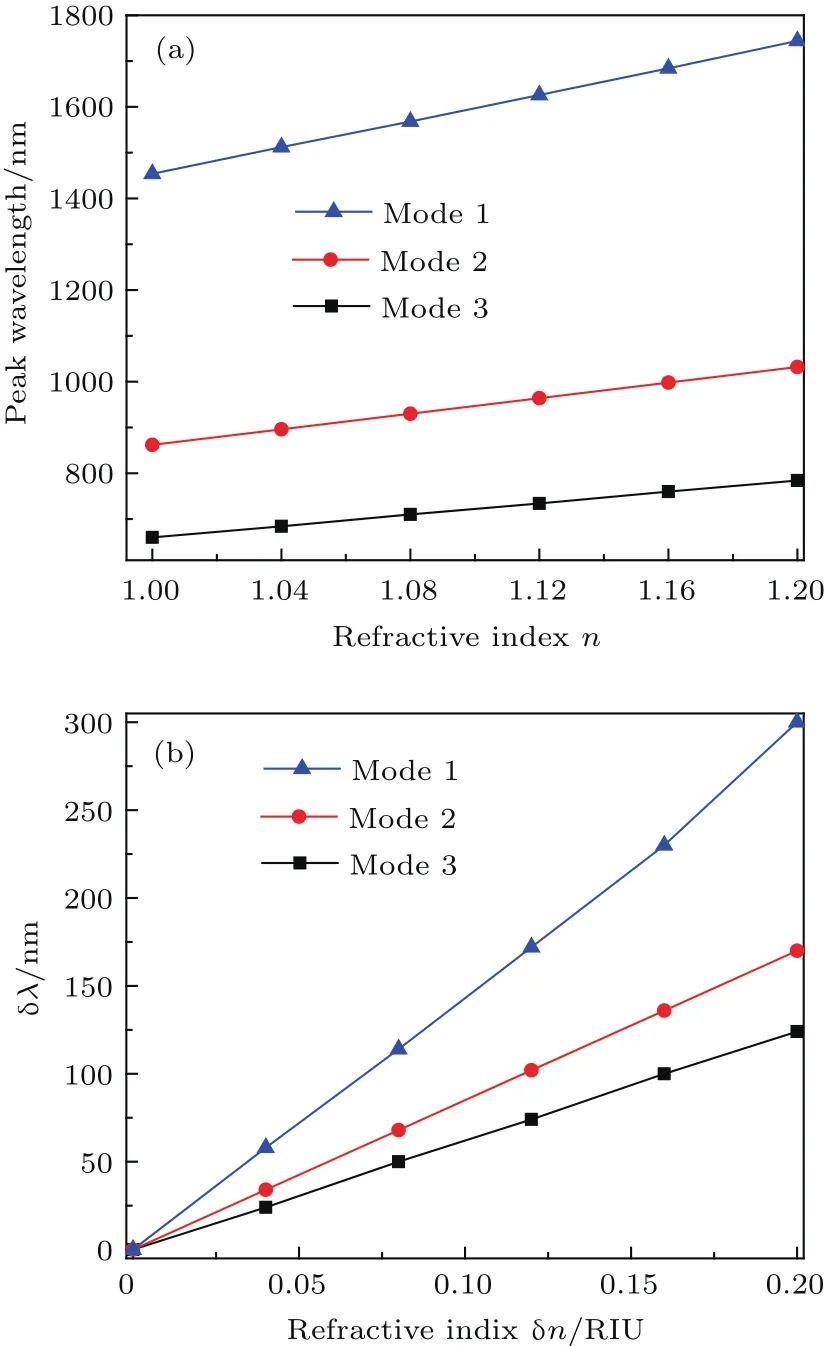
图5 (a)三种透射峰模式下共振波长与折射率n的关系；(b)三种模式下共振峰偏移量δλ随折射率增加量δn的变化关系Fig.5.(a)The three peaks of transmission spectrum versus the refractive index n；(b)shift in the three resonance peaks as a function of the refractive index change(δn).Here,R=200 nm,w=50 nm,and d=10 nm.

为了研究环形谐振腔中心半径R对图2结构光学传输特性的影响,我们计算了不同半径R时的透射光谱.图6(a)为半径R=170,190,210,230 nm时的透射谱.由图6(a)可以看出,Mode 1和Mode 2下对应共振波长随半径增大发生明显红移,且对应峰值减小.由于金属的损耗是不可避免的,透射率不能达到1,随着传播长度的增加,损耗增大[27],所以Mode 1和Mode 2的峰值强度随着R的增大而下降.Mode 1,2和3对应于(5)式中的一阶,二阶和三阶贝塞尔函数的本征解.从图3(a)可以看出,Mode 1和Mode 2的透射强度比较大,随半径增大发生对应峰值强度变小的现象比较明显,而Mode 3本身的透射强度较小,随半径的增大几乎没有峰值强度的变化.更重要的原因是从图3(b)可以看出Mode 1在环形谐振腔中磁场Hz分布显示有一对驻波共振模式,从图3(d)可以看出Mode 2在环形谐振腔中磁场Hz分布有两对驻波共振模式,它们之间相互耦合,对于耦合到后面的MIM直波导的透射有增强作用,弥补了一部分因半径增大带来的损耗,因此Mode 2比起Mode 1峰值强度下降的速率变慢.同理,Mode 3在环形谐振腔中磁场Hz分布有三对驻波共振模式,它们的耦合作用更强,导致Mode 3的强度不随着R增大而下降.图6(b)显示了三种模式的谐振波长随半径增大的关系.由图6(b)看出谐振波长与环形腔半径几乎成线性关系,其中,图中实心点为仿真值,实线为曲线拟合结果.可以看出,传输特性可以通过改变环形腔中心半径容易调谐.而且由图6(b)可见,三种模式对应波长彼此分开,它们之间的间隔足够大,对于峰值波长可以在相当大的范围内(500—1800 nm)变化.因此,对于不同类型的波导带通滤波器可以仅仅通过改变环的半径来实现.此外,该结构简单,尺寸小,在纳米器件设计方面也有潜在的应用前景.这些结果将为设计带通滤波器提供一定的理论基础.

此外,我们研究了波导与环形腔的间距d对SPPs传输特性的影响.如图7所示,保持R=200 nm,w=50 nm,和n=1不变,环形腔与波导间距d由10 nm增加到25 nm时的透射谱.由图7可以看出,随着间距d的增大透射强度明显减小,透射峰均发生蓝移,并且透射带宽减小,这与文献[27]中的结果是一致的.因此,可以通过控制环形腔与波导的耦合距离来调谐透射强度及透射带宽.

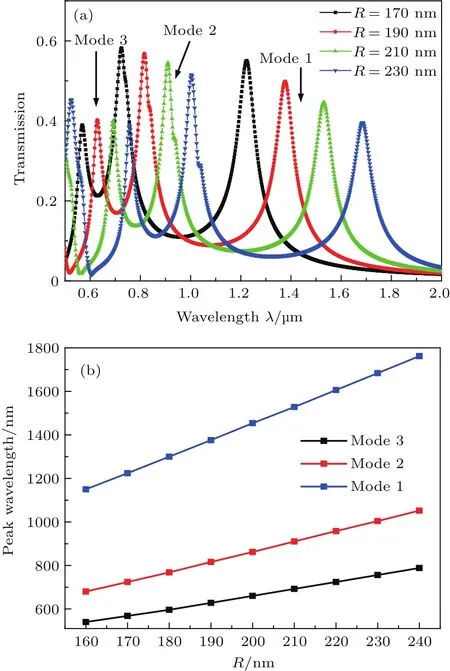
图6 (a)环形腔中心半径R不同时的透射谱；(b)三种模式下共振峰波长随环腔中心半径R变化关系Fig.6.(a)Transmission spectra of the structurefor different R；(b)relationship between the three resonance peaks wavelengths and the radius of ring cavity.Here,d=10 nm,and n=1.

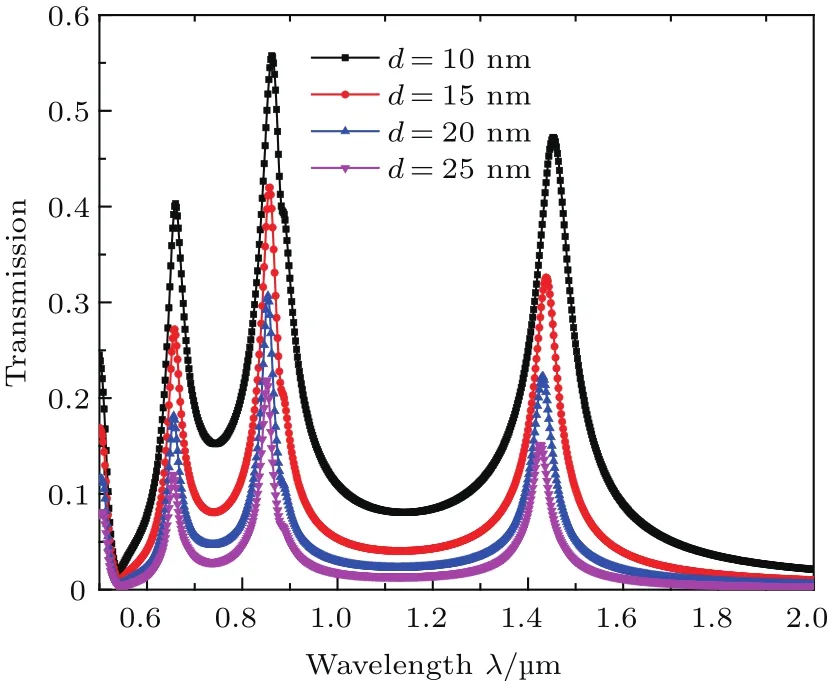
图7 环形腔与波导间距d变化时的透射谱Fig.7.Transmission spectra with different d.Here,R=200 nm,w=50 nm.

4 结 论

本文用有限元方法数值研究了一个基于十字连通形环形谐振腔MIM波导的SPPs传播特性.结果表明:透射光谱中透射峰是由于SPPs在环形谐振腔中发生共振所引起,每一个透射峰对应于谐振腔中的一种谐振模式；共振中心波长可以通过环形腔中心半径和填充介质折射率进行调谐,且共振波长与环形腔中心半径和介质折射率的变化呈线性关系,透射强度和透射带宽都随着波导与环形腔间距的增大而减小,可以通过控制环形腔与波导的耦合距离来调谐透射强度及透射带宽.该结构因其体积小及易于集成的优势,可广泛应用于光学器件中,并且能获得较高的传感灵敏度.此外,该器件可作为较大波长范围的可调谐带通滤波器.理论上计算了环形谐振腔的特征波长,计算结果与数值结果符合较好.研究结果对于高灵敏度纳米级折射率传感器和带通滤波器的设计具有重要意义.

感谢西北师范大学物理与电子工程学院严春满副教授和兰州理工大学理学院王向贤副教授的讨论.