波导谐振腔Fano共振特性研究
孟颖,宋建林,夏鹏飞,马良,刘彻
(长春理工大学 光电工程学院,长春 130022)
波导谐振腔Fano共振特性研究
孟颖,宋建林,夏鹏飞,马良,刘彻
(长春理工大学光电工程学院,长春130022)
利用耦合模理论,建立了波导-谐振腔-波导谐振腔耦合的数学模型,并给出了此系统的光学透过率和相移特性的解析表达式,分析了此系统的Fano共振物理机制,即由波导谐振腔驻波模式的共振与谐振腔模式之间的共振耦合引起的,另外还给出了Fano共振模式所需要满足的位相匹配条件,同时分析了各个性能参数对此系统的透过率特性和位相特性影响。
Fano共振;谐振腔;波导;耦合模理论
波导谐振腔耦合系统由于其具有非常突出的共振特性,可以用来设计多种光子学器件,如光分束器[1,2],交叉连接器[3,4]和分插复用滤波器[5-7]等。谐振腔与波导之间的正耦合和侧耦合具有互补的透过率特性和相同的位相变化特性,谐振腔与谐振腔的级联形成耦合共振波导(CROW)[8],基于谐振腔模式耦合的光子学器件与特性近些年来已经成为光子学领域的研究热点。
有限长波导可以形成类似于F-P谐振腔,在其中形成驻波模式,通过改变波导的长度,可以很方便的调节模式的共振频率,其与谐振腔之间的耦合也非常简便,只要控制其与谐振腔之间的距离就可以实现,然而,波导谐振腔的耦合特性目前研究的比较少[9],主要是由于传统的波导谐振腔的泄露损耗比较大,端面的反射率比较低。随着加工技术的发展,光子晶体波导和谐振腔已近成为集成光学中的研究热点,光子晶体波导谐振腔可以克服传统波导谐振腔的常见缺陷,研究其光学特性对于光子学器件的设计和发展具有潜在的指导价值。
本文利用耦合模理论,建立了谐振腔波导耦合系统的数学模型,给出了透过率和位相变化的数学表达式,分析了Fano共振的物理机制和Fano共振的位相匹配条件,同时还分析了不同参数对这些特性的影响。
1 理论分析
为了分析波导谐振腔-谐振腔-主波导互耦合光学特性,建立的光学系统模型如图1所示,其中波导谐振腔的长度为L,模式传输常数为β;S+ij和S-ij(j=1,2)分别为谐振腔波导、主波导的入射和出射的归一化幅度。考虑光波仅从波导输入端入射(S+22=0),且为时谐波时,即具有ejωt的形式,采用时域耦合模理论[10],此系统的光学特性可以表示为:其中a为谐振腔的归一化谐振幅度,ω0为谐振腔的谐振频率,分别为谐振腔向波导谐振腔和主波导的衰减速率。


图1 波导谐振腔-谐振腔-主波导互耦合模型
波导谐振腔中,从谐振腔波导耦合端耦合到谐振腔中的入射波s+11是从谐振腔中耦合出来的光波经另一端发射回来的,所具有位相关系为:
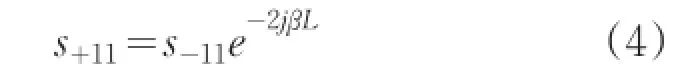
联立方程(1)-(3),并结合方程(4),主波导的透过系数可表示为:
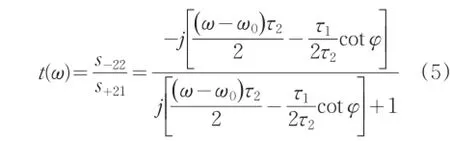
其中φ=β(ω)L为光在波导谐振腔中的相移。
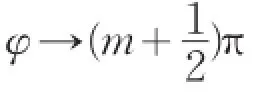
2 透过率特性分析
由式(5)可以给出图1所示的光学耦合系统的透过率特性,即:
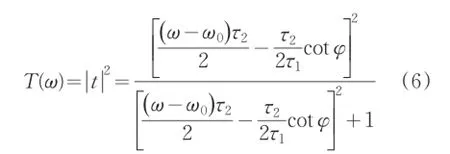
从式(6)可知,而当φ→mπ时,透过率恒为1,这是由于波导谐振腔中进入的与返回的行波叠加形成驻波模式,此模式与谐振腔模式相互耦合,引起谐振腔模式的分裂,在此波长上引起Fano共振;另外,从式中还可以看出,当入射波的频率满足关系式时,透过率变为零,所有的入射光全部被反射,如果此波长在φ=mπ附近,可以从透过谱中看到两个全反谷。
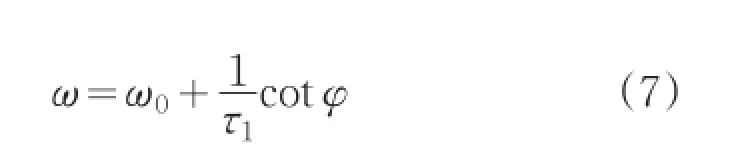
为了进一步研究透过率与频率之间的关系,假设谐振腔波导满足线性色散关系,在频率变化范围不大的情况下,采用自由空间近似,表示为:

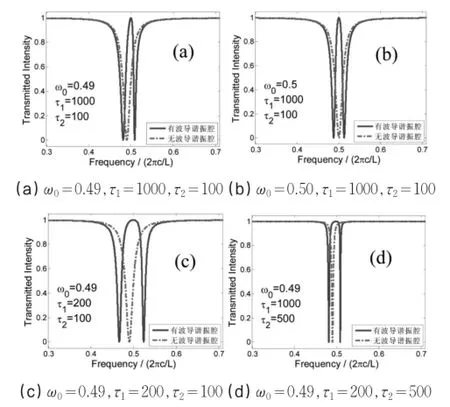
图2 波导谐振腔耦合系统透过率的理论曲线
图2给出了不同参数情况下此系统的透过率随频率的变化关系,本文采用归一化频率2πc/L为单位,其中实线表示耦合系统的透过率,虚线表示没有波导谐振腔的情况。从图2(a)-(d)可以看出,透过率曲线具有两个明显的特征:第一个特征是无论参数怎么变化,在频率ω0=0.50(2πc/L)处透过率始终为1,这是因为在该处,由式(7),谐振腔波导的相移始终为φ=mπ,谐振腔波导正好形成共振驻波模式,产生了Fano共振;第二个特征是单个谐振腔形成了透过率曲线的包络,而波导谐振腔以驻波共振为界,引起模式的分裂,两个反射峰位于驻波共振频率的两侧。
比较图2(a)和(b),当谐振腔共振频率改变时,由此谐振腔确定的包络曲线将随之移动,另外,由式(7)知道,两个反射峰的位置也随之改变,改变幅度与谐振腔的共振频率的改变量相同,两个反射峰之间的频率间隔保持不变。
谐振腔向谐振腔波导耦合时,衰减系数对反射峰的位置具有决定性的影响,如图2(c)所示,两个反射峰之间的间距会变大,从式(7)也能看出此特点,τ1变小,反射峰的位置远离包络中心ω0,两反射峰之间的间距与谐振腔的衰减速率1 /τ1成正比,当然,由于谐振腔波导的相移包含频率项,也对反射峰的位置有一定的影响。
谐振腔向主波导的衰减系数决定了透过率曲线的包络,当衰减速率1 /τ2变小时,包络会变窄,由式(7)知,反射峰的位置与此衰减速率无关,所以反射峰的位置不随此衰减的变化而变化,由图2(a)和(d)知,反射峰之间的间隔不变。
通过上面的分析我们知道,波导谐振腔的Fano共振是由于波导谐振腔的驻波模式的激发引起谐振腔共振模式的分裂,而驻波模式的位相关系固定,所以Fano共振的位置不变。
3 位相特性分析
此波导谐振腔耦合系统的位相关系也可以由式(9)给出:
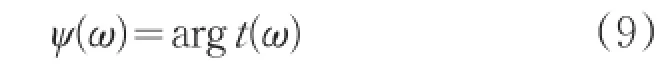
图3给出了不同参数情况下相移随频率的变化关系。还是采用归一化频率2πc/L为单位,实线表示耦合系统的透过率,虚线部分给出了只有谐振腔,没有波导谐振腔的情况。从图中可以看出,在Fano共振处,位相有一个2π的突变,这是由于数学上反函数引起的,所以我们可以看出,有Fano共振情况下,相移的改变量为4π,与只有单个谐振腔的2π不同,所以此波导谐振腔的相移空间比单个谐振腔大一倍。
由式(5)知道,在透射谷的位置,位相的变化率最快,即单位频率改变情况下,位相的变化量更大。在每一个反射峰的位置,位相的该变量为2π,即在反射峰的上升沿和下降沿变化都是π。反射峰越窄,位相的变化率越快,如图5(a)和(d)右边的反射峰所示;当反射曲线的包络越宽,位相的变化率越慢,这是由于总的位相变化率量一定,反射峰间距越大,位相的变化率越慢,如图5(c)所示。当波导谐振腔中驻波模式的共振频率与谐振腔的共振频率一致时,反射峰两侧的位相变化速率一致,这是由于此时的反射谱是对称的,如图3(b)所示。

图3 波导谐振腔耦合系统位相变化的理论曲线
通过上面的分析我们知道,波导谐振腔的Fano共振相移是单个谐振腔的两倍,模式分裂,即Fano共振位置的两侧分别为2π。
4 结论
利用耦合模理论,建立了主波导-谐振腔-波导谐振腔耦合系统的光学特性模型,给出了Fano共振的物理机制和位相匹配条件,同时分析了此耦合系统透过率特性和位相特性与各个性能参数的关系,研究结果表明,Fano共振的频率完全由位相匹配条件确定,其它参数只能改变Fano共振特性曲线的形状,而不能改变Fano共振的频率位置。
[1] Fan S,Johnson S G,Joannopoulos J D,et al.Waveguidebranchesinphotoniccrystals[J].Opt.Soc. Am.B,2001,18(2):162-165.
[2] Zhou Jianhong,Chang Qing,Mu Da,et al.Theoretical investigation of waveguide power splitters with parallel output ports in two-dimensional square-lattice photonic crystals[J].Opt.Soc.Am.B,2009,26 (1):2469-2471.
[3]Johnson S G,Manolatou C,Fan S,et al.Elimination ofcrosstalkinwaveguideintersections[J].Opt. Lett.,1998,23(23):1855-1857.
[4]ZhouJianhong,DiXu,MuDa,etal.Improved broad bandwidth intersections in photonic crystals[J]. Opt.Comm,2012,285(1):38-40.
[5]Fan S,Villeneuve P R,Joannopoulos J.D,et al. Channel drop tunneling through localized states[J]. Phys.Rev.Lett,1998,80(5):960-963.
[6] Ren HL,Jiang C,Hu WS,et al.Channel drop filter in two-dimensional triangular lattice photonic crystals,[J].Opt.Soc.Am.A,2007,24(10):9-13.
[7]Ren HL,Jiang C,Hu WS,et al,Photonic crystal channel drop filter with a wavelength-selective reflection micro-cavity[J].Opt.Expr,2006,14(6):2446-2458.
[8] Yariv A,Xu Y,Lee R K,et al.Coupled-resonator optical waveguide:a proposal and analysis[J].Opt. Lett,1999,24(11):711-713.
[9]Zhou Jianhong,Xu Xiping,Han Wenbo,et al.Fano resonance of nanoparticles embedded in Fabry-Perot cavities[J].Optics Express,2013,21(10):12159-12164.
[10]Haus H A.Waves and fields in optoelectronics [M].Taibei:Central Book Company,1985.
Transfer Matrix Method for Cascaded Cavity-waveguide Coupling System
MENG Ying,SONG Jianlin,XIA Pengfei,MA Liang,LIU Che
(School of Optoelectronic Engineering,Changchun University of Science and Technology,Changchun 130022)
The optical properties of waveguide-cavity coupling system were investigated by using coupled-mode theory,where the mechanism of Fano resonance is originated from the coupling between the cavity mode and the standing wave mode in the waveguide resonator.The phase-match conditions for Fano resonance are obtained and the dependence of the transmissions and phase shifts on the functional parameters are also analyzed.
Fano resoance;cavity;waveguide;coupled-mode theory
O436
A
1672-9870(2015)06-0064-03
2015-10-22
孟颖(1980-),女,硕士,实验师,E-mail:quiet_brook@aliyun.com

