AlH+离子5个Λ-S态和10个Ω态的光谱性质以及激光冷却的理论研究∗

2018-11-03 04:31邢伟孙金锋施德恒朱遵略

物理学报 2018年19期

关键词：势阱常数修正

邢伟孙金锋施德恒朱遵略

1)(河南科技大学材料科学与工程学院,洛阳 471023)

2)(信阳师范学院物理电子工程学院,信阳 464000)

3)(河南师范大学物理与材料科学学院,新乡 453007)

(2018年5月9日收到；2018年7月10日收到修改稿)

1 引言

AlH+离子在天体物理方面扮演重要的角色.在稠密和扩散的星际分子云中,AlH+离子是形成星际分子AlH的中间产物,离子分子化学反应过程如下:首先Al+和H2或H反应产生AlH+:Al++H2→AlH++H,Al++H→AlH++H2；接着AlH+和其他的H2反应产生AlH:AlH++H2→ AlH+H；离解电子复合AlH产生AlH:AlH+e→ AlH+H[1].此外,AlH+离子是非常有前途的激光冷却材料[2,3].这些方面的研究,是以AlH+离子电子态的光谱性质和跃迁性质为基础的.

在过去的几十年里,实验上对AlH+离子的光谱性质进行了广泛研究[3−12]. 早在1933—1934年,Holst[4,5]研究了360 nm时A2Π →X2Σ+跃迁,并认为A2Π是倒转态.随后,Almy和Watson[6]以及Raf i等[7]驳斥了Holst的假设,他们研究了A2Π→X2Σ+跃迁的(0-0)和(1-1)波带,证实了A2Π为正常态.1984年,Balfour和Lindgren[8]在研究AlD+离子A2Π→ X2Σ+跃迁时顺便整合了Almy和Watson[6]的实验数据.1986年,Müller和Ottinger[9]研究了Al++H2→ AlH+(A2Π,B2Σ+)+H的化学发光反应,观察了A2Π→X2Σ+跃迁很多新的波带,决定了A2Π和X2Σ+态的部分光谱常数.此外,他们也观察了B2Σ+→X2Σ+跃迁,但未报道B2Σ+态的光谱常数.两年后,Müller和Ottinger[10]重新分析先前实验数据[6,7],报道了AlH+离子X2Σ+和A2Π态新的光谱常数.2011年,Szajna和Zachwieja[11]观察了27000—29000 cm−1范围内A2Π → X2Σ+跃迁(0-0)和(1-1)波带的全部转动结构,报道了X2Σ+的分子常数,他们的结果比Balfour和Lindgren[8]的稍微精确.2014年,Seck等[12]利用共振增强多光子解离方法对AlH+离子进行了转动态分析,此外,他们又利用多参考单双组态相互作用(MRSDCI)方法和aug-cc-pCVQZ基组分别计算了X2Σ+,A2Π,B2Σ+,C2Σ+和D2Π态的势能曲线(PECs)和它们之间的跃迁偶极矩(TDMs),遗憾的是他们未拟合得到这些态的光谱常数和态-态之间跃迁的Franck-Condon因子(fυ′υ′′)和自发辐射寿命(τυ′)等.同年,Lien等[3]利用电子激励宽带激光器同时驱动不同转动能级的冷却共振技术囚禁冷却AlH+离子到它的基振转量子态,并获得了驱动X2Σ+(υ′′=0)→ A2Π1/2(υ′=0)跃迁的激光波长λ00、它们之间的能量间隔(T0),X2Σ+态υ′′=0与υ′′=1的能级间隔(∆G1/2)和A2Π1/2(υ′=0)的辐射宽度(Γr).

理论方面,1977年,Rosmus和Meyer[13]利用赝势自然轨道组态相互作用(PNOCI)和耦合电子对(CEPA)方法计算了X2Σ+态平衡核间距(Re)附近的PEC,并获得了它的光谱常数.1981年,Guest和Hirst[14]利用多参考双激发组态相互作用(MRDCI)方法和高斯基计算了2Π和2Σ+态的PECs,并获得了这些态的光谱常数.1982年,Klein等[15]利用多组态自洽场方法(MCSCF)方法计算了X2Σ+,A2Π和B2Σ+态的PECs和它们之间的TDMs,拟合得到光谱常数以及A2Π(υ′=0) → X2Σ+(υ′′=0)和B2Σ+(υ′=0)→ X2Σ+(υ′′=0)跃迁的爱因斯坦自发辐射系数(Aυ′υ′′), 另外, 他们又利用赝自然轨道组态相互作用与耦合电子对(PNOCEPA)方法获得了X2Σ+和A2Π态的光谱常数.2008年,Li等[16]采用自旋轨道耦合(SOC)作用下多组态准简并微扰理论(SO-MCQDPT)计算了AlH+离子X2Σ+,A2Π1/2和A2Π3/2态的PECs,并得到了它们的光谱常数. 2011年,Nguyen等[2]利用EOM-CC3/augcc-pCVQZ和MRCI/aug-cc-pCVQZ理论分别计算了X2Σ+,A2Π和B2Σ+态的PECs和它们之间的TDMs,并获得了这3个态的光谱常数和A2Π(υ′=0)的 τυ′. 2017年,Ferrante等[17]利用冻结核FCI/CBS理论计算了AlH+离子X2Σ+态的PEC,计算中考虑了核相关、相对论和对角化Born-Oppenheimer的贡献,并对X2Σ+态的光谱常数做了最好的估算.总结现有的实验和理论计算,我们发现:1)对于Λ-S态,现有的实验和计算集中于研究X2Σ+和A2Π态光谱常数和分子常数；2)对于Ω态,实验上,仅Balfour和Lindgren[8]获得了A2Π 态的SOC常数Aυ′(υ′=0,1)；理论上,仅Li等[16]对A2Π态进行了SOC效应研究；另外,Wu等[18]对等电子的MgH自由基前两个离解极限所包含的5个Λ-S和10个Ω态光谱特性的研究表明,SOC效应对MgH自由基A2Π和B2Σ+态的PECs和光谱常数的影响是明显的；然而迄今为止,未有实验和理论计算对AlH+前两个离解极限所对应的5个Λ-S和10个Ω态的光谱特性进行系统的研究；3)虽然Nguyen等[2]和Lien等[3]分别获得了忽略SOC效应时AlH+离子激光冷却方案以及驱动X2Σ+(υ′′=0)→ A2Π1/2(υ′=0) 跃迁的λ00和A2Π1/2(υ′=0)的Γr,但为了评价激光冷却分子离子的可行性和冷却效果[19−23],需要系统地计算相关Ω态之间跃迁的fυ′υ′′和振动分支比(Rυ′υ′′),激发Ω态的τυ′和Γr,驱动X2Σ+1/2(υ′′) 到激发Ω(υ′)跃迁的激光波长 (λυ′′υ′)和回弹温度 (Trecoil).

本文第2部分简要介绍所使用的计算方法；第3部分报道AlH+离子前两个离解极限Al+(1Sg)+H(2Sg)和Al+(3Pu)+H(2Sg)所对应的5个Λ-S和10个Ω态的PECs；讨论基组的收敛性以及芯电子价电子相关和标量相对论修正对光谱常数的影响；预测束缚和准束缚Λ-S和Ω态的光谱常数(激发能Te,离解能De,Re,谐振频率ωe,非谐振动常数ωexe,平衡转动常数Be和振转耦合常数αe)和振动能级G(υ)；评价激光冷却AlH+离子的可行性和冷却效果,计算2(1/2)(υ′) → X2Σ(υ′′)和A2Π3/2(υ′) → X2Σ(υ′′)跃迁的 fυ′υ′′和 Rυ′υ′′,驱动X2Σ(υ′′=0-2) → 2(1/2)(υ′=0,1)和X2Σ(υ′′=0-2) → A2Π3/2(υ′=0,1)跃迁的λυ′′υ′(λ00,λ10 和λ21)和Trecoil, 以及2(1/2)(υ′=0,1)和A2Π3/2(υ′=0,1)的τυ′和Γr；讨论SOC效应对光谱常数、G(υ)和激光冷却AlH+的影响；第4部分给出结论.

2 计算方法

Al原子和H原子基态的电离能分别为48278.47和109678.73 cm−1[24]. 因此,AlH+离子的第一离解极限为Al+(1Sg)+H(2Sg).Al+和H原子第一激发态的能级分别为37474.91和82259.10 cm−1[24].所以,AlH+离子的第二离解极限为Al+(3Pu)+H(2Sg).利用Wigner-Witmer定则,这两个离解极限产生5个Λ-S态.我们把这些态连同它们的离解极限列入表1中.为了便于比较,这两个离解极限能量差的实验值也列入表1.

AlH+离子X2Σ+,A2Π,B2Σ+,a4Π和b4Σ+态电子结构是在MOLPRO 2010.1程序包[25]C2v点群中计算的.在核间距1.002—10.802 Å范围内,首先采用 Hatree-Fock自洽场(HF SCF)方法得到AlH+离子X2Σ+态的初始猜测分子轨道和波函,然后使用态平均的完全活性空间自洽场(CASSCF)方法对初始猜测分子轨道和波函进行优化,最后用考虑Davidson修正的内收缩多参考组态相互作用(icMRCI+Q)方法[26,27]计算AlH+离子5个Λ-S态的PECs.为提高这些态PECs的精度,利用aug-cc-pV5Z(AV5Z)和 aug-cc-pV6Z(AV6Z)基组[28,29]将势能外推至完全基组极限(CBS)(记为icMRCI+Q/56)；CBS时的总能量采取参考能和相关能分别外推公式[30]得到:

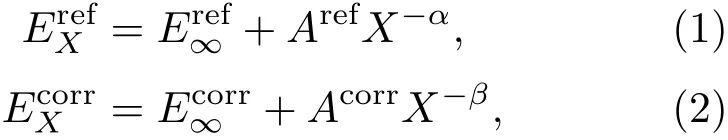
其中,X是aug-cc-pVXZ(AVXZ)基组的基数,E和E分别是由AVXZ基组计算的参考能和相关能的能量；和E分别是外推至CBS时参考能和相关能的能量；对于给定的分子,Aref和Acorr是常数；外推系数α和β分别为3.4和2.4.α和β通过拟合和优化得到,因此用(1)和(2)式外推时,会产生一些残余误差.

利用cc-pCVTZ(CVTZ)[31]和cc-pV5Z-DK[32,33]基组分别将芯电子价电子相关和标量相对论修正包含到PECs中.将CBS时的总能量加上经芯电子价电子相关修正和标量相对论修正的结果,便得到考虑外推和这两种修正后的AlH+离子5个Λ-S态PECs(记为icMRCI+Q/56+CV+DK),并把这些态PECs绘在图1中.在我们以前的研究[34]中已详细给出了芯电子价电子相关和标量相对论修正的方法.计算步长取0.2 Å,在Re附近,为获得PECs的细节信息,步长取0.02 Å.在CASSCF及其随后的icMRCI+Q计算中,我们选择6个分子轨道(4a1,1b1和1b2)作为活性空间,对应于Al+3s3px3py3pz4s和H 1s轨道.Al+3s2电子和H 1s1电子作为价电子.也就是说,这个活性空间由3个价电子和6个分子轨道组成,记为CAS(3,6).其余的10个内核电子则放入5个闭壳层轨道(3a1,1b1和1b2)中,对应于AlH+离子的1—3σ和1π分子轨道.另外,Al+离子1s2s2p闭壳层的10个电子用于芯电子价电子相关效应计算.图2给出了利用CASSCF/AV6Z计算获得的活性分子轨道能量随核间距变化的曲线.由图2可知,在1.002—2.112 Å的范围内,6σ和7σ轨道的能量非常接近,并且X2Σ+,A2Π和B2Σ+态的势阱分布在这个区域,所以活性空间中包含7σ轨道是十分必要的.当采用这11个轨道(7a1,2b1和2b2)进行计算时,在目前的核间距范围内所得的PECs既光滑、又收敛.所以,在本文的计算中,活性空间选为CAS(3,6).

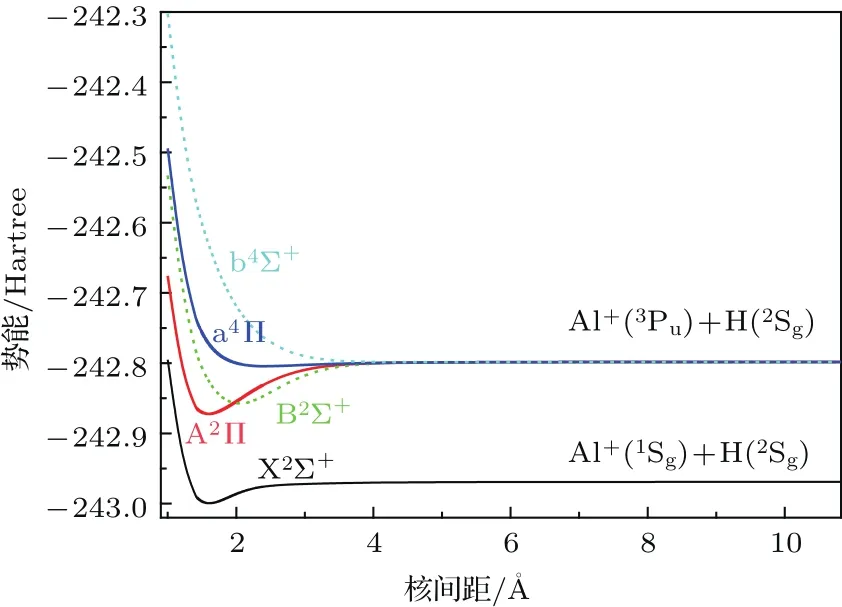
图1 AlH+离子5个Λ-S态的PECsFig.1.PECs of 5 Λ-S states of the AlH+cation.

表1 icMRCI+Q/56+CV+DK理论水平上获得的5个Λ-S态离解极限处的相对能量Table 1.Relative Energies of the 5 Λ-S states in the dissociation limits at the level of icMRCI+Q/56+CV+DK.

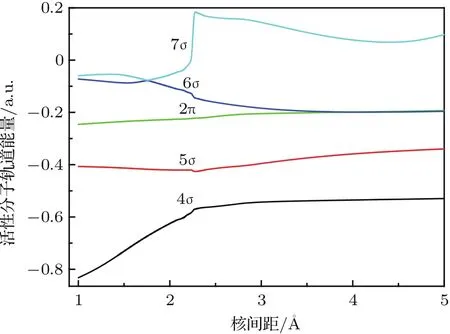
图2 AlH+离子活性分子轨道随核间距的变化Fig.2.The active molecular orbital energies of AlH+along the internuclear separation.

在相同的计算条件下,采用非收缩全电子CVTZ基组,通过态相互作用方法,利用完全Breit-Pauli SOC算符(SO)来考虑SOC效应的贡献,从而得到icMRCI+Q/CVTZ理论水平上Ω态的PECs.将SOC效应贡献的能量(记为SOC)加到icMRCI+Q/56+CV+DK的势能中,便得到icMRCI+Q/56+CV+DK+SOC理论水平上10个Ω态的PECs.

利用上述方法,我们决定了icMRCI+Q/56+CV+DK理论水平上Al+(1Sg)+H(2Sg)和Al+(3Pu)+H(2Sg)的能量差值,由表1可知,本文所计算的这两个离解极限的能量差值为37426.82 cm−1,这与Al原子多重态3Pu能级实验数据的平均值37474.91 cm−1符合得很好.

3 结果与讨论

3.1 基组的收敛性以及芯电子价电子相关和标量相对论修正对光谱常数的影响

任何高精度的计算,基组必须具有收敛性.否则,由于可靠性差和精度低,计算结果所确定的光谱结果则不太重要.由于篇幅的限制,我们仅以icMRCI+Q 理论获得的X2Σ+态 Re,ωe和De(如表2所列)为例,简要讨论基组的收敛性.

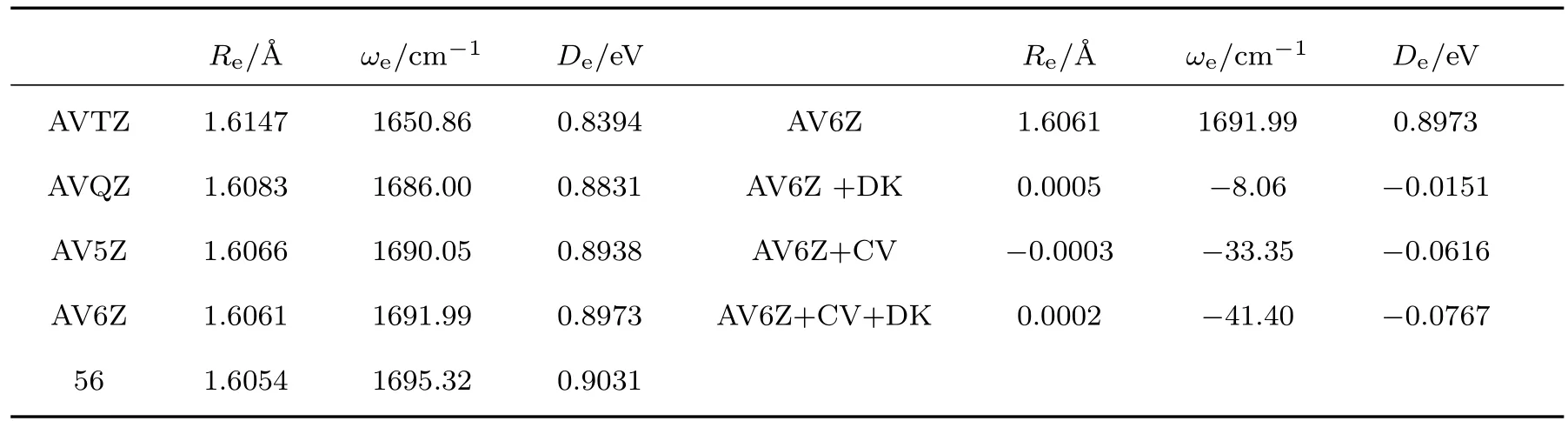
表2 在icMRCI+Q理论水平,基组收敛性、芯电子价电子相关和标量相对论修正对X2Σ+态的光谱常数的影响Table 2.Convergence observations of basis set as well as the effect of core-valence correlation and scalar relativistic corrections on the spectroscopic parameters for the X2Σ+states at the icMRCI+Q level of theory.

随着基组的基数增大(从AVTZ到AVQZ,从AVQZ到AV5Z,再从AV5Z到AV6Z),在各自Re处,势能分别降低713.51,207.40和54.43 cm−1,当外推AVXZ至AV∞Z时,势能降低86.25 cm−1.显然,X2Σ+态Re处的势能相对于基组具有很好的收敛性.类似于Re处的势能,X2Σ+态Re和ωe值相对于基组也是收敛的.如表2所列,随着基组的基数增大,Re值分别减小0.0064,0.0017和0.0005 Å,ωe值分别增大35.14,4.05和1.94 cm−1.当把基组从AVXZ外推到AV∞Z时,Re值减小不超过0.0007 Å,ωe值增加不超过4 cm−1. 因此,Re和ωe值相对于基组具有较快的收敛性.

类似于X2Σ+态,A2Π,B2Σ+和a4Π的光谱常数相对于基组也具有很好的收敛性.由于篇幅的限制,本文对此不做详细讨论.总之,本文的计算相对于基组具有很好的收敛性.

下面以基于icMRCI+Q/AV6Z计算获得的X2Σ+态光谱常数(如表2所列)为例,讨论芯电子价电子相关和标量相对论修正对结果的影响.由表2可知,仅考虑DK修正时,Re增大了0.0005 Å,ωe和De分别减少了8.06 cm−1和0.0151 eV；仅考虑CV修正时,Re,ωe和De分别减少了0.0003 Å,33.35 cm−1和0.0616 eV；可见,两个修正对ωe和De值的影响是明显的.同时考虑这两种修正时,Re增大了0.0002 Å,ωe和De分别减少了41.40 cm−1和0.0767 eV.由此可得,当进行高精度计算时,必须考虑这两个修正.

根据以上讨论,我们将利用icMRCI+Q/56+CV+DK方法计算的PECs进行以下的光谱计算.

3.2 5个Λ-S态的PECs和光谱常数

由图1可知,5个Λ-S态PECs的特征为:1)X2Σ+,A2Π,B2Σ+和a4Π为束缚态且具有1个的势阱；2)b4Σ+态为排斥态.

基于icMRCI+Q/56+CV+DK计算的PECs,利用LEVEL 8.0程序[35],本文获得AlH+离子X2Σ+,A2Π,B2Σ+和a4Π态的光谱常数(Te,De,Re,ωe,ωexe,Be和αe)和G(υ). 为了便于讨论,把本文计算的这4个Λ-S的光谱常数连同实验值[10]和理论结果[2,13−17]以及Re处的主要电子组态列入表3.

表3 icMRCI+Q/56+CV+DK理论水平上AlH+离子4个Λ-S态的光谱常数Table 3.Spectroscopic parameters of the 4 Λ-S states of AlH+cation at level of icMRCI+Q/56+CV+DK.

AlH+离子X2Σ+态Re附近主要价电子组态为4σ25σ12π06σ07σ0(0.9225), 其他电子组态所占的权重很小. 它的阱深为6663.47 cm−1,有10个振动态,G(υ)分别为813.20,2327.85,3657.60, 4750.83, 5554.36, 6029.59, 6299.84,6478.32,6589.59和6644.71 cm−1.本文的 ∆G1/2为1514.65 cm−1,与Lien等[3]的结果1500 cm−1符合得很好.另外,本文计算的Re,ωe和Be与实验值[10]也十分符合,它们与实验值[10]的偏离分别为0.0006 Å (0.037%),4.25 cm−1(0.257%)和0.02312 eV(0.343%)；由表3可知,仅Nguyen等[2]和Ferrante等[17]报道的Re和Be比本文稍微接近实验值[10].虽然本文的ωexe和αe分别比实验值[10]小13.88和0.0972 cm−1,但与Ferrante等[17]最好的估算结果接近.迄今为止,没有实验报道精确的De值,本文的计算值0.8264 eV与Nguyen等[2]的0.8318 eV符合.

A2Π态也是典型的束缚态,其阱深为16223.56 cm−1, 有18个G(υ)(856.07,2507.01,4080.66, 5532.17, 6930.38, 8247.86, 9479.90,10630.15,11690.76,12655.53,13517.50,14271.57,14909.49,15421.17,15796.32,16031.16,16150.17和16203.72 cm−1). 由表3可知,A2Π态Re附近主要价电子组态分别来自于X2Σ+态5σ→ 2π和4σ→2π的单电子激发,因此这个态具有多参考特征.Balfour和Lindgren[8]以及Klein等[15]报道了A2Π(υ′=0)与X2Σ+(υ′′=0)的T0,利用本文所得这两个态的Te,ωe和ωexe值以及公式Te=T0+1/2(ωe′′−ωe′)+1/4(ωex−ωex),我们得到T0值为27958.82 cm−1,这比实验值[8]大238.98 cm−1,百分比误差为0.0862%.本文A2Π态的Re,ωe和Be与实验值[10]也符合得很好,它们分别偏离实验值[10]0.0015 Å (0.094%),13.82 cm−1(0.791%)和0.00141 cm−1(0.141%).由表3可知,仅Nguyen等[2]报道的ωe和ωexe,Guest和Hirst[14]报道的αe比本文稍微接近实验值[10].

B2Σ+态也具有多参考特征,它的Re附近主要价电子组态分别来自于X2Σ+态4σ→5σ和5σ→6σ的单电子激发.它的阱深为12874.60 cm−1,包含15个G(υ)(629.73,1924.61,3189.29,4394.73,5552.48, 6653.45, 7690.06, 8660.89, 9558.97,10376.16,11103.87,11730.82,12240.69,12613.63和12832.81 cm−1).仅有3组理论[2,14,15]报道了这个态的光谱常数.与计算值[2,14,15]相比,本文的Te和De稍大,ωe,ωexe和αe稍小,计算[2,14,15]＜Re＜计算[14,15],计算[14,15]＜Be＜计算[2].

需要注意的是理论结果[2,14,15]是用单一基组计算,然而本文结果是在icMRCI+Q/56+CV+DK理论上得到的.因此,本文B2Σ+态的结果也应是精确和可靠的.

X2Σ+态电子组态中一个电子从4σ→ 2π的激发产生a4Π态,a4Π态阱深为1341.65 cm−1,包含7个振动态,G(υ)分别为217.22,579.69,865.76,1074.91,1211.34,1290.65和1329.65 cm−1.

3.3 10个Ω态的PECs和光谱常数

考虑SOC效应后,AlH+离子5个Λ-S态将产生10个Ω态,包含1个Ω = −1/2态、5个Ω =1/2态、3个Ω=3/2态和1个Ω=5/2态；Al+第一激发态3Pu分裂为3P0,3P1和3P2成分,因此离解极限Al+(1Sg)+H(2Sg)和Al+(3Pu)+H(2Sg)分别分裂成1条和3条渐近线.我们把这4个离解极限和它们所产生的10个Ω态离解极限处的相对能量列入表4.由表4可知,本文利用icMRCI+Q/56+CV+DK+SOC得到的AlH+离子3P0—1S0,3P1—1S0和3P2—1S0的能级间隔分别比实验值[24]小43.48,46.59和54.19 cm−1,百分比误差分别为0.116%,0.124%和0.144%.10个Ω态的PECs连同它们的离解极限绘于图3中.

图3 AlH+离子10个Ω态的PECs(a)Ω=−1/2和Ω=1/2以及(b)Ω=3/2和Ω=5/2Fig.3.PECs of 10 Ω states of the AlH+cation for the(a)Ω = −1/2 and Ω =1/2 along with(b)Ω =3/2 and Ω=5/2.

表4 AlH+离子前两个离解极限所产生的10个Ω态的离解关系Table 4.Dissociation relationships of the 10 Ω states generated from the first two dissociation asymptotes of the AlH+cation.

基于icMRCI+Q/56+CV+DK+SOC计算的PECs,利用LEVEL 8.0程序[35]获得8个Ω态(它们产生于X2Σ+,A2Π,B2Σ+和a4Π态)的光谱常数和G(υ),如表5所列.为了便于讨论,我们把仅有的理论结果[16]以及各自Re处主要的Λ-S态权重也列入表5.

考虑SOC效应后,X2Σ+态未分裂.在整个核间距区域,X2Σ完全来自于X2Σ+态,因此,X2Σ的光谱常数(De,Re,ωe,ωexe,Be和αe)和G(υ)几乎等同于X2Σ+态相应的值.

表5 利用icMRCI+Q/56+CV+DK+SOC理论计算获得的8个Ω态的光谱常数Table 5.Spectroscopic parameters obtained by the icMRCI+Q/56+CV+DK+SOC calculations for the 8 Ω states generated from the X2Σ+,A2Π,B2Σ+,and a4Π states.

由图1可知,A2Π与 B2Σ+态相交于R=1.9696 Å.SOC效应使A2Π与B2Σ+态PECs的交叉变成2(1/2)与3(1/2)PECs的避免交叉(如图3(a)所示).这个避免交叉诱导:1)2(1/2)态有1个势垒和2个势阱(这2个势阱分别用上标第一势阱和第二势阱表示)；2)3(1/2)态在避免交叉点附近出现1个势阱.对于2(1/2)态,势垒出现在R=1.9820 Å,并且势垒顶部的势能低于离解极限处的势能；2(1/2)第一势阱态主要来自A2Π态,它的阱深为3445.31 cm−1,包含2个G(υ),855.88和2498.60 cm−1；2(1/2)第二势阱态主要来自B2Σ+态,它的阱深为100.74 cm−1,不包含任何振动态.对于3(1/2)态,其主要的Λ-S成分从R=1.9220 Å处的B2Σ+(99.92%)变化到R=2.0220 Å处的A2Π (99.78%),它的阱深为12645.25 cm−1,包含14个G(υ)(1229.76,3198.14,4736.15, 6136.28, 7370.45, 8474.05, 9457.94,10313.90,11040.63,11635.78,12093.25,12408.54,12577.21和12641.00 cm−1).

A2Π态分裂出的A2Π3/2Ω成分,由于与其他的Ω态之间不存在避免交叉现象,因此,A2Π3/2态的PEC与A2ΠΛ-S态的PEC的形状相同.它的阱深为16086.61 cm−1,包含17个振动态,G(υ)分别为855.91,2506.49,4079.75,5530.93,6928.77,8245.77,9477.20,10626.74,11686.49,12650.32,13511.25,14264.10,14900.50,15409.92,15780.46,15996.35和16072.34 cm−1. 由表3和表5知,A2Π3/2态的Te,Re, ωexe和αe分别比A2Π态相应的值增大了51.36 cm−1,0.0001 Å,0.05 cm−1和0.0002 cm−1；然而ωe,Be和De分别降低了0.29 cm−1,0.00066 cm−1和0.0174 eV.

Balfour和Lindgren[8]获得的A2Π态的A0和A1值分别为108.21和107.5 cm−1,结合公式Aυ=Ae−αAe(υ+1/2),获得平衡SOC常数Ae的实验值为108.57 cm−1.本文计算的Ae仅比实验[8]小6.30 cm−1,优于Li等[16]的结果204.32 cm−1.Li等[16]还计算了A2Π1/2和A2Π3/2态的PECs和其他光谱常数Re,ωe,ωexe,Be,αe和De,由于未考虑A2Π1/2与B2Σ态PECs的避免交叉,计算的2(1/2)态PEC的形状与本文的不同.由表5可知,对于2(1/2)第一势阱态,本文的T0为27908.73 cm−1,偏离实验值[3]91.27 cm−1(0.326%)；本文的Re稍小于Li等[16]的结果,∆G1/2和De稍大于Li等[16]的结果；对于A2Π3/2态,本文的Re,ωe和ωexe稍小于Li等[16]的结果,Be,αe和De稍大于Li等[16]的结果.

SOC效应使a4Π分裂为4个Ω态,按能量增加的顺序为a4Π−1/2,4(1/2)(a4Π1/2),a4Π3/2和a4Π5/2；由表5可知, 从a4Π−1/2到a4Π5/2态两个相邻Ω态之间的Ae分别为37.09,37.32和37.53 cm−1. 由表3和表5可知,SOC效应对每一个Ω态Re,ωe,ωexe,Be,αe和De的影响并不大,例如,4个Ω态的Re,ωe,ωexe,Be,αe和De与a4Π态相应值的最大偏离分别为0.0002 Å,0.373 cm−1,0.67 cm−1,0.00106 cm−1,0.0035 cm−1和0.0053 eV.同时,SOC效应对a4Π−1/2,a4Π3/2和a4Π5/2态的G(υ)的影响也不大, 但对4(1/2)(a4Π1/2)态的G(υ)产生了影响,即,4(1/2)(a4Π1/2)态有6个振动态,G(υ)分别为217.18,579.51,865.78,1078.49,1241.71和1361.65 cm−1.

考虑SOC效应后, b4Σ+分裂为5(1/2)(b4Σ)和b4Σ+3/2态,这两个Ω态仍是排斥态.

3.4 2(1/2)↔X2Σ,A2Π3/2↔X2Σ+1/2跃迁和激光冷却循环

由3.3节的讨论可知,X2Σ和A2Π3/2Ω态的PECs与相应Λ-S态PECs的形状相同,2(1/2)Ω态PEC的形状发生了明显的变化.因此,A2Π3/2→ X2Σ的TDM曲线(TDMC)与A2Π →X2Σ+的TDMC的形状相同；然而,在R＞1.9696 Å的核间距区域内,2(1/2)→ X2Σ的TDMC的形状发生了明显的变化,如图4所示. 在R=1.602 Å,A2Π → X2Σ+,2(1/2) → X2Σ和A2Π3/2→ X2Σ的TDMs分别为0.62835,0.62858和0.62811 a.u.,可见它们是强的跃迁.另外,由图4可知,当核间距R＞4.0 Å,这三对跃迁的TDMs趋近于零渐近线.

SOC效应对A2Π态的Ae、2(1/2)态的PECs和光谱常数以及2(1/2)→X2ΣTDMC的影响是明显的.因此,我们仅考虑基于SOC效应的AlH+离子的激光冷却循环.

由于2(1/2)第二势阱不包含任何振动态,A2Π3/2(υ′＞2)的振动态与3(1/2)(υ′＞0)振动态之间存在强的相互作用,因此,为了评价激光冷却AlH+离子的可行性,本文利用LEVEL 8.0程序[35]仅获得了2(1/2)第一势阱(υ′=0,1)和A2Π3/2(υ′=0,1)到X2Σ(υ′′) 态跃迁的 fυ′υ′′,表6列出了2(1/2)第一势阱(υ′=0,1)和A2Π3/2(υ′=0,1)到X2Σ(υ′′)跃迁的 fυ′υ′′和 Rυ′υ′′以及驱动X2Σ+1/2(υ′′=0-2) 到2(1/2)第一势阱(υ′=0,1)和A2Π3/2(υ′=0,1)跃迁的激光波长(λυ′′υ′).

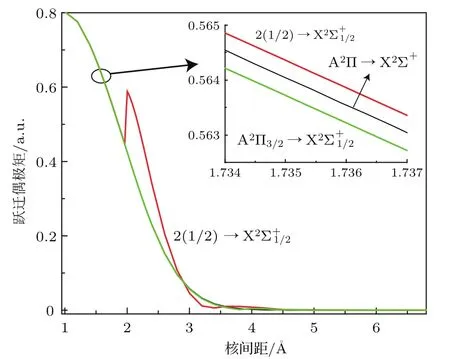
图4 AlH+离子2(1/2)→X2Σ+1/2,A2Π3/2→ X2Σ+1/2和A2Π→X2Σ+的TDMCsFig.4.TDMCs of the 2(1/2)→ X2Σ,A2Π3/2 →X2Σ+1/2and A2Π → X2Σ+transitions of AlH+cation.

由表6可知,对于2(1/2)第一势阱(υ′)↔X2Σ+(υ′′)跃迁,2(1/2)第一势阱(υ′=0,1)→ X2Σ(υ′′)有高度对角化的fυ′υ′′(f00=0.9939 和f11=0.9707),相应的R00=0.9803 和R11=0.9467；当υ′′＞3时,分支比记为R03+,并且R03+＜1.28×10−5；驱动X2Σ(υ′′=0) → 2(1/2)第一势阱(υ′=0)跃迁的主循环激光的波长λ00为358.74 nm,与Lien等[3]的实验值360 nm符合得很好；振动分支比R01为0.0192,因此,我们需要1束再抽运激光(λ10=379.27 nm)来驱动X2Σ(υ′′=1) →2(1/2)第一势阱(υ′=0)的跃迁；同时,我们注意到振动分支比R12有大的比率,因此,为了使该离子保持在准闭合激光冷却循环系统中,需要第2束再抽运激光(λ21=374.86 nm)；对于第2束再抽运激光,在AlH+离子的G(υ)增加之前,有Nscat=1/R03+＞7.81×104光子被散射；另外,这3束激光冷却波长(λ00=358.74 nm,λ10=379.27 nm和λ21=374.86 nm)都在紫外区域,连续波长的激光辐射可以通过钛宝石激光器的倍频输出产生.类似地,A2Π3/2(υ′=0,1)→ X2Σ(υ′′)跃迁也有高度对角化的fυ′υ′′(f00=0.9938和f11=0.9609),相应的R00=0.9798和R11=0.9266；当υ′′＞3时,R03+＜6.90×10−6；另外,R01和R12也有大的比率；因此,驱动X2Σ(υ′′)→ A2Π3/2(υ′)跃迁同样需要3束激光,激光波长分别λ00=357.43 nm,λ10=377.80 nm和λ21=373.26 nm.

除高度对角化分布的fυ′υ′′和Rυ′υ′′之外, 光循环速率显著(105—108s−1)是另一个直接冷却分子离子的条件.通常,激发态足够短的τυ′(10−9—10−6s)能快速的实现激光冷却.然而,较长的τυ′意味着较窄的Γr,这导致较小的回弹能量,从而使分子离子达到较低的温度.因此,为了达到满意的冷却效果,必须仔细地平衡τυ′和Γr.表7列出了2(1/2)第一势阱(υ′=0,1)→ X2Σ+(υ′′)和 A2Π3/2(υ′=0,1)→ X2Σ(υ′′) 跃迁的τυ′和Γr.

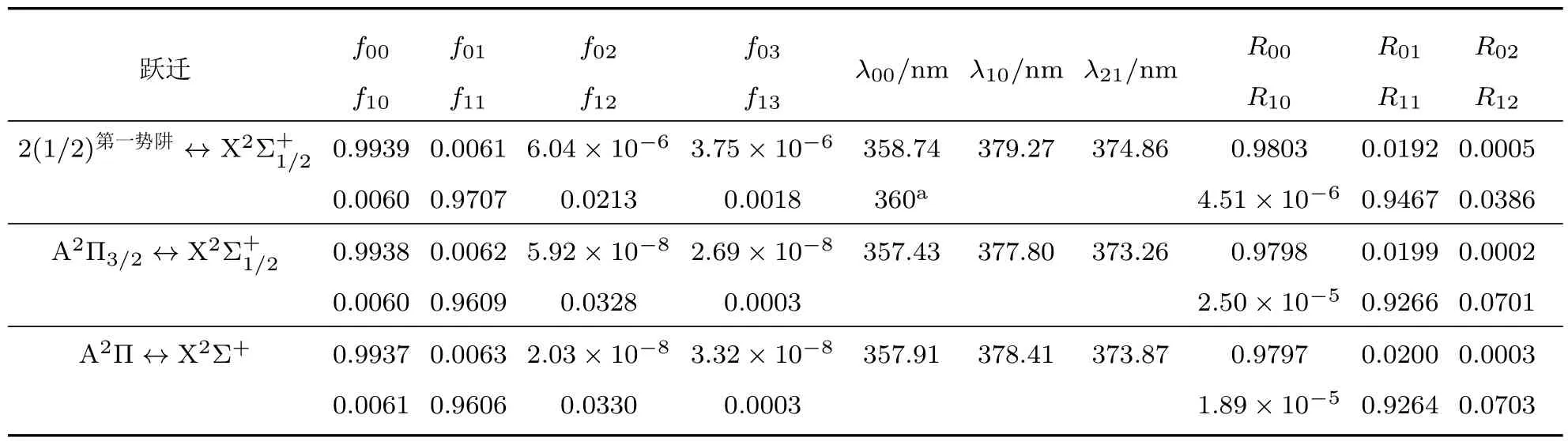
表6 2(1/2)第一势阱(υ′)↔ X2Σ(υ′′),A2Π3/2(υ′) ↔ X2Σ(υ′′)和 A2Π(υ′) ↔ X2Σ+(υ′′)跃迁的Franck-Condon 因子(fυ′υ′′),波长 (λυ′′υ′)和振动分支比 (Rυ′υ′′)Table 6.The calculated Franck-Condon factors(fυ′υ′′),wavelength(λυ′′υ′),and vibrational branching ratios(Rυ′υ′′)of the 2(1/2)1st well(υ′)↔ X2Σ+1/2(υ′′),A2Π3/2(υ′) ↔ X2Σ(υ′′),and A2Π(υ′) ↔ X2Σ+(υ′′)transitions.

a,文献[3]中的实验值.

跃迁 f00 f01 f02 f03 R00 R01 R02 f10 f11 f12 f13 λ00/nm λ10/nm λ21/nm R10 R11 R12 2(1/2)第一势阱 ↔ X2Σ+1/20.9939 0.0061 6.04×10−63.75×10−6 358.74 379.27 374.86 0.9803 0.0192 0.0005 0.0060 0.9707 0.0213 0.0018 360a 4.51×10−60.9467 0.0386 A2Π3/2↔ X2Σ+1/2 0.9938 0.0062 5.92×10−82.69×10−8 357.43 377.80 373.26 0.9798 0.0199 0.0002 0.0060 0.9609 0.0328 0.0003 2.50×10−50.9266 0.0701 A2Π ↔ X2Σ+ 0.9937 0.0063 2.03×10−83.32×10−8 357.91 378.41 373.87 0.9797 0.0200 0.0003 0.0061 0.9606 0.0330 0.0003 1.89×10−50.9264 0.0703

表7 2(1/2)第一势阱(υ′=0,1)↔ X2Σ,A2Π3/2(υ′=0,1)↔ X2Σ和A2Π (υ′=0,1)↔ X2Σ+跃迁的τυ′,Γr 和TrecoilTable 7.Spontaneous radiative lifetimes(τυ′),radiative width(Γr)and recoil temperatures(Trecoil)for the 2(1/2)1st well(υ′=0,1)↔ X2Σ(υ′′),A2Π3/2(υ′=0,1) ↔ X2Σ(υ′′)and A2Π(υ′=0,1) ↔ X2Σ+(υ′′)transitions.

a,文献[3]中的实验值；b,文献[2]中的计算值.

2(1/2) → X2Σ+1/2 A2Π3/2→ X2Σ+1/2 A2Π → X2Σ+0 59.3 8.95×10−5 8.94×10−5a 5.31 58.8 9.03×10−5 5.35 59.1 59.16b 8.98×10−5 5.34 1 62.8 8.45×10−5 62.9 8.44×10−5 63.2 8.40×10−5

由表7可知,本文计算的2(1/2)第一势阱(υ′=0,1)的τυ′分别为59.3和62.8 ns,相应的Γr分别为8.95× 10−5和8.45× 10−5cm−1；A2Π3/2(υ′=0,1)的τυ′分别为58.8和62.9 ns, 相应的Γr分别为9.03× 10−5和8.44× 10−5cm−1. 本文计算的2(1/2)第一势阱(υ′=0)的Γr仅比实验值[3]大1.00×10−7cm−1,百分比误差为0.112%.因此,这些短的τυ′和窄的Γr能快速激光致冷AlH+离子.此外,为了评价冷却效果,我们计算了X2Σ+(υ′′= 0 )→ 2(1/2)第一势阱(υ′=0)和X2Σ(υ′′=0) →A2Π3/2(υ′=0)的Trecoil[Trecoil=h2/(mkBλ2)],它们的值也列于表7.由表7可知,它们分别为5.31和5.35µK,显然,这是令人满意的冷却温度.

为了评价SOC效应对激光冷却AlH+的影响,表6和表7也列出了A2Π(υ′=0,1) ↔X2Σ+(υ′′) 的fυ′υ′′,Rυ′υ′′,λυ′′υ′,τυ′,Γr 和Trecoil.因2(1/2)第一势阱(υ′= 0,1)和A2Π3/2(υ′= 0,1)主要来自于A2Π态,SOC效应对激光冷却AlH+的影响不大. 以2(1/2)1stwell(υ′) ↔ X2Σ(υ′′)跃迁为例, 对于2(1/2)第一势阱(υ′= 0,1) →X2Συ′′)跃迁, 它的f00,f11,R00和R11分别比A2Π(υ′=0,1) → X2Σ+(υ′′)跃迁相应的值大0.0002(0.020%),0.0101(1.051%),0.0006(0.061%)和0.0203(2.191%),2(1/2)第一势阱(υ′= 0,1)的τυ′和Γr与A2Π (υ′= 0,1)相应值的偏离分别为0.2 ns(0.338%),3× 10−7cm−1(0.334%),0.2 ns(0.633%)和5× 10−7cm−1(0.595%)；对于X2Σ(υ′′) → 2(1/2)第一势阱(υ′)跃迁, 所需三束激光的波长分别比X2Σ+(υ′′) → A2Π (υ′)跃迁相应的值大0.83 nm(0.232%),0.86 nm(0.227%)和0.99 nm(0.265%),此外,X2Σ(υ′′=0) →2(1/2)第一势阱(υ′=0)的Trecoil比X2Σ+(υ′′=0)→ A2Π (υ′=0)的Trecoil小0.03 µK(0.562%).