例谈数列求和的几种常见方法

■河南郑州外国语学校 田 景

数列求和是历年高考的热点,也是数列章节的重点,具有灵活多变、综合性强的特点。下面结合一些高考真题和常见题目,对数列求和的常用方法进行汇总整理,供同学们参考。

1.公式法

若题目中已明确知道数列的类型,或经过判断发现是等差数列或等比数列,我们可以直接用公式法求其前n项和,等比数列的求和公式中需要讨论公比是否为1。

例1 （2017·北京）已知等差数列{an}和等比数列{bn}满足a1=b1=1,a2+a4=10,b2b4=a5。

（1）求{an}的通项公式;

（2）求和:b1+b3+b5+…+b2n-1。

解析：（1）易得an=2n-1,过程略。

（2）设公差为d,由（1）知a5=a1+4d=9,等比数列{bn}满足b1=1,b2b4=9,可得b3=3（-3舍去）,则{b2n-1}是以b1=1为首为公比的等比数列,所以b1+b3+

2.错位相减法

错位相减法是在推导等比数列前n项和时用到的一种方法,主要用来求数列{an·bn}的前n项和,其中{an}为等差数列,{bn}为等比数列。求和时,将已知和式乘以等比数列{bn}的公比,然后再将所得和式与原和式错位相减,转化为同倍数的等比数列进行求和。使用时要注意:（1）要考虑公比为1的特殊情况;（2）错位相减时勿遗漏末项;（3）相减后,Sn前的系数不要忘记除掉;（4）算出结果后最好代入n=1,2进行检验。

例2 （2017·山东）已知{an}是各项均为正数的等比数列,且a1+a2=6,a1a2=a3。

（1）求数列{an}的通项公式;

（2）{bn}为各项非零的等差数列,其前n项和为Sn,已知S2n+1=bnbn+1,求数列前n项和Tn。

解析：（1）记正项等比数列{an}的公比为q,因为a1+a2=6,a1a2=a3,所以（1+q）a1=6,q=a1q2。解得q=0（舍去）,或a1=q=2,所以an=2n。

3.并项求和法

若一个数列相邻两项或几项的和是定值或者有一定的规律,我们可以把这两项或者几项合并成一项,然后形成一个新的数列,再对新的数列进行求和,这种方法叫并项求和法。并项是利用加法的交换律和结合律将“不规则的和”转化为“规则的和”,化繁为简。

例3 （2016·天津）已知数列{an}满足an=2n-1,若对任意的n∈N+,bn是log2an和log2an+1的等差中项,求数列}的前2n项和。

解析：因为bn是log2an和log2an+1的

4.裂项相消法

裂项相消法是将数列的通项拆成两项或者几项的差,在求和过程中相互抵消,最后只留下有限项的和,此种方法的难点在于通项的拆分。常见的拆项公式有:

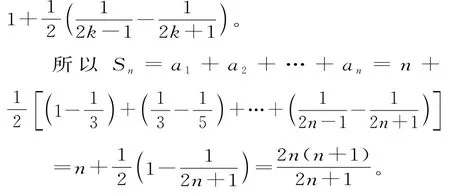
5.倒序相加法

这个方法是推导等差数列前n项和时常用的方法,适用于与首末两项等“距离”两项的和是一个常数或者有一定的规律的数列。具体操作:将这个数列倒过来排列,然后再和原来的数列对应项相加,即第一项和最后一项相加,第二项和倒数第二项相加…,可以得到n项的和,这n项之间有规律可循,即可求和。

数列的求和方法千变万化,同学们要想能很好地解决此类问题,掌握本文总结的几种基本方法是关键。当然这里只是简单地讲述了一些高中阶段常见的基本类型,同学们在做题时可以根据题目的具体特征选择合适的方法转化为这几种简单的形式求解。希望本文对同学们掌握数列求和有所帮助。