行进间粗对准误差分析方法

王律化，石志勇，宋金龙，王海亮

(陆军工程大学石家庄校区，河北 石家庄 050001)

0 引言

初始对准是确定惯性导航系统初始的姿态、位置、速度等导航参数。按照对准过程，分为粗对准和精对准两个阶段。为提高初始对准过程中载体的机动性，要求惯性导航系统能够在载体行驶时完成粗对准过程。

针对上述问题，文献[1]运用惯性空间为参考标准，分三步建立粗对准姿态矩阵。文献[2—6]主要是利用里程计作为辅助测量手段，通过信息融合的方法解算姿态矩阵。文献[7—8]将姿态矩阵的求解转化为wahba问题，通过最优解的方法，解算姿态矩阵。

上述方法对于粗对准姿态矩阵的求解过程进行了详细说明，但是鲜有文献对粗对准过程中载体行驶速度、晃动角速度、加速度计零位偏差和陀螺常值漂移误差与粗对准失准角之间的关系进行说明。

粗对准失准角的大小直接决定了后续精对准过程中所使用的误差方程。因此，研究上述四个量和粗对准失准角之间的关系，对于行进间初始对准的研究，具有重要意义。针对此问题，本文在分析基于惯性系行进间粗对准方法的基础上，提出了载体行进间粗对准误差分析方法。

1 行进间粗对准算法原理

根据文献[1]中的方法，行进间粗对准算法如下

(1)

(2)

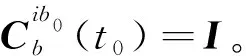
(3)

(4)

2 粗对准误差分析

对于式(1)进行扰动得：

(5)

(6)

(7)

(8)

将式(6)—式(8)带入式(1)，并且忽略二阶小项，得：

(9)

由式(9)可知

(10)

(11)

对式(11)进行积分得：

(12)

(13)

式(13)中，

(14)

(15)

对式(4)进行变形得：

(16)

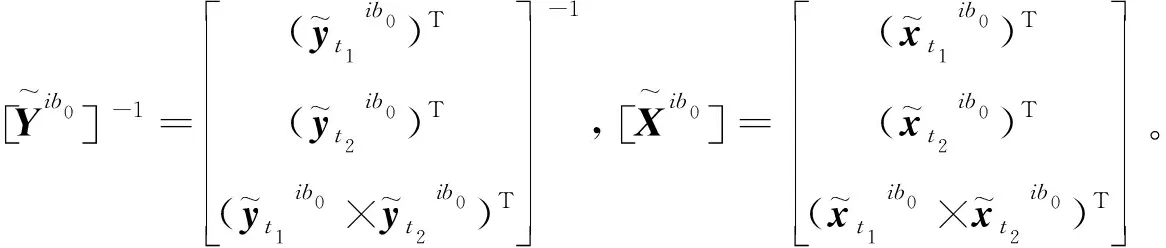
将式(14)带入到式(16)中得

(17)

对比式(15)可得

(18)

所以

(19)

(20)

(21)

将式(20)代入到式(21)中，得到如下等式

(22)

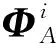
(23)

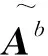
(24)

将式(24)带入到xib0的等式中，得：

(25)

(26)

(27)

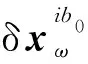
(28)

将式(12)带入到式(28)中得

(29)

对于上式中的sin(ωietk)和cos(ωietk)运用Taylor展开，由于粗对准的工程中，所用到的时间较短，所以略去二阶以上的项，得：

sin(ωietk)=ωietk

(30)

(31)

将式(30)和式(31)带入到式(29)

(32)

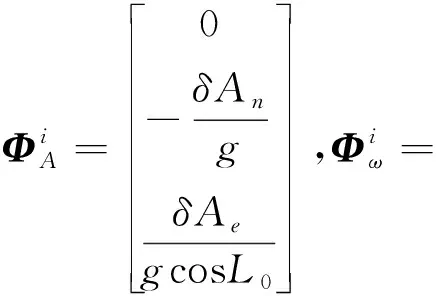
(33)

(34)

(35)

M=2[(cotL0An+Au)εe+cotL0Aeεn+Aeεu]

(36)

由于整个粗对准的时间较短，可以假设式(30)和式(31)中的sin(ωietk)和cos(ωietk)分别为0和1，

带入到式(13)、式(34)和式(35)中得：

(36)

(37)

(38)

式(38)中，δAn=εeve-εuvu+ωeγe-ωuγu+n；δAe=-εevn+εnvu-ωeγn+ωnγu+e。

当载体处在静止状态时，式(38)转变成下列等式

(39)

对比文献[11]的结果和式(39)，在静止的条件下，本方法的结果和解析法的结果相同。因为在解算载体行进间粗对准姿态矩阵时，其本质是双矢量定姿原理，当载体处在静止状态时，不论是采用解析法还是基于惯性系的行进间粗对准，所能得到的极限精度应该是相同的。但是解析法粗对准只能使用于载体处在静止状态下，而基于惯性系的行进间粗对准可以在载体运动的条件下完成对准工作，因此有着更广泛的应用前景。

3 仿真分析

载体在完成行进间粗对准的过程中，行驶速度、晃动角速度、加速度计零位偏差和陀螺常值漂移都对最终的对准结果有影响。为简化分析，主要以不同条件下的东向水平失准角对准结果为例，对比各个条件对粗对准结果的影响。

3.1 速度影响仿真

假设载体总的运动时间为600 s，为验证算法的有效性，进行100次的仿真。假设载体的初始位置为45.235 1°N/85.268 4°E，高度0 m，陀螺为激光陀螺，其常值漂移为0.015(°)/h，随机漂移为0.001(°)/h，加速度计常值零偏为450 μg，随机漂移为10 μg，里程计的刻度系数误差为2‰，采样时刻t1=60 s，t1=480 s，其载体速度分别为：2 m/s和6.5 m/s。仿真结果如图1—图2所示。

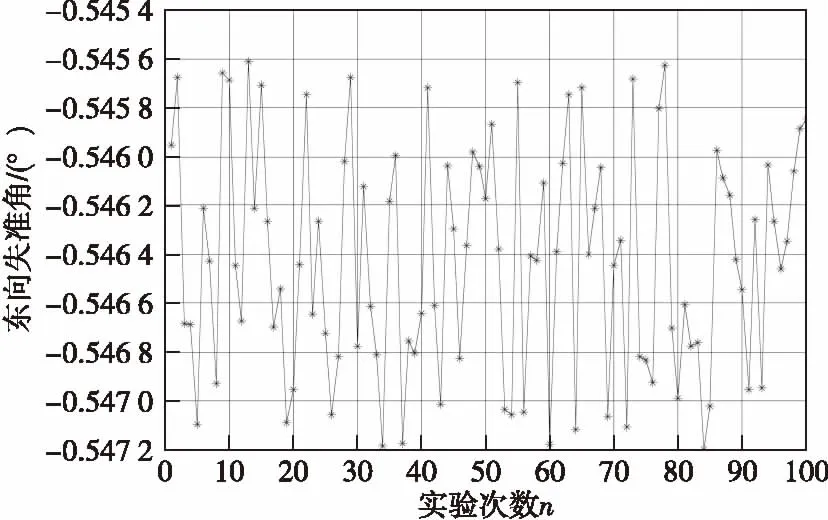
图1 速度为2 m/s时东向失准角Fig.1 East misalignment angle when velocity is 2 m/s

图2 速度为6.5 m/s时东向失准角Fig.2 East misalignment angle when velocity is 6.5 m/s

对比图1和图2仿真结果，当载体的运动速度从2 m/s变为6.5 m/s时，由于速度的改变，其东向失准角从-0.546 4°变成了-0.756 3°,由于速度变为了原来的3.25倍，使得失准角扩大了38.4%。可见由于载体在粗对准过程中速度的增加，使得对准的精度降低，因此，行进间粗对准的过程中，应当尽量降低载体的行驶速度，以保证对准精度。

3.2 载体晃动影响仿真

为检验载体晃动角度对于对准结果的影响，假设载体一直保持2 m/s的速度，载体晃动的角速度分别为1 rad/s和5 rad/s的仿真结果如图3所示。

图3 晃动速度为1 rad/s和5 rad/s时东向失准角Fig.3 East misalignment angle when waggle is 1 rad/s and 5 rad/s

通过对比载体在不同晃动角速度下东向失准角的仿真结果，发现东向失准角对于载体在不同晃动角速度下的变化不敏感。这说明基于惯性系的粗对准方法可以有效地隔离由于载体晃动所引起的对准误差。

3.3 加速度计零偏影响仿真

为检验载体晃动角度对于对准结果的影响，载体的其他假设不变，速度保持2 m/s，同时假设加速度计的零位偏差从450 μg变为600 μg，仿真结果如图4所示。

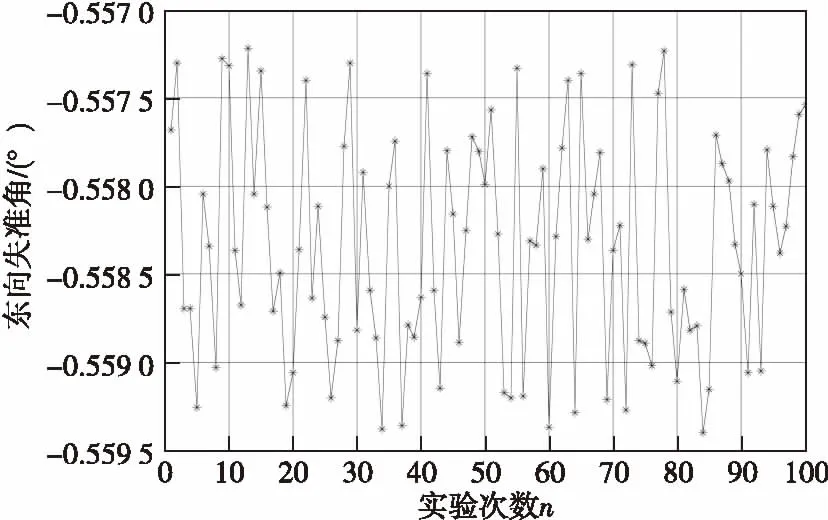
图4 加速度计零偏为600 μg时东向失准角Fig.4 East misalignment angle with the accelerometer bias is 600 μg

对比图2和图4，当单纯改变加速度计零位偏差的时候，东向失准角度数随着零位偏差值的增大而增大，东向失准角的均值从-0.546 4°变为了-0.558 3°，加速度计的零位偏差增加了33%，其他条件不变的情况下，失准角度数扩大了2.18%。可见随着加速度计零偏值的变大，对准结果中东向失准角的度数也在增大。

3.4 陀螺常值漂移影响仿真

为检验载体晃动角度对于对准结果的影响，载体的其他假设不变，速度保持2 m/s，同时假设陀螺的常值漂移从0.01(°)/h变为0.02(°)/h，仿真结果如图5所示。

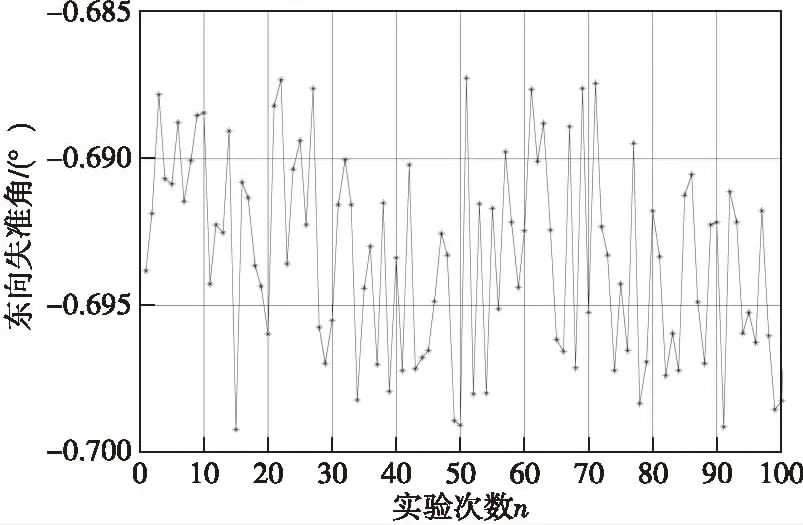
图5 陀螺常值漂移为0.02(°)/h时东向失准角Fig.5 East misalignment angle with the gyroscope bias is 0.02 (°)/h

4 结论

本文提出了载体行进间粗对准误差分析的方法，该方法在分析基于惯性系行进间粗对准方法的基础上，以里程计作为辅助测量手段，通过微分扰动法，详细分析了载体行驶速度、晃动角速度、加速度计零位偏差和陀螺常值漂移误差与粗对准失准角之间的关系。仿真实验表明，载体行进间粗对准的结果主要受到载体在进行粗对准过程中行驶速度和惯性测量器件本身精度的影响，而载体晃动对于对准结果没有明显影响。可见基于惯性系的行进间粗对准可以有效地隔离载体的晃动影响。同时，为提高粗对准的精度，在条件许可的情况下，可以降低载体的行驶速度以提高对准精度。