磁场压缩波动幅度对卫星磁强计零位标定影响的数值仿真

王国强，潘宗浩，胡小文，刘 凯，孟立飞，易 忠，张铁龙

（1.哈尔滨工业大学（深圳） 空间科学与应用技术研究院，深圳 518055； 2.中国科学院 月球与深空探测重点实验室，北京 100101； 3.中国科学技术大学 地球和空间科学学院，合肥 230026；4.北京卫星环境工程研究所，北京 100094； 5.奥地利科学院 空间研究所，格拉茨 A-8042）

0 引言

精确的磁场测量对揭示磁重联和地球磁层动力学过程等空间现象具有重要意义[1-6]。卫星上的磁通门磁强计测量的磁场包含卫星剩磁、磁强计零位偏移和自然磁场[7-9]，为精确获得自然磁场，需要从磁强计所测的磁场中剔除卫星剩磁和磁强计的零位偏移[10]。卫星剩磁可进一步分为动态磁场和稳态磁场，其中稳态磁场变化较为缓慢，故可将其和磁强计的零位偏移一起视为磁强计的零位补偿[11]；动态磁场可采用双点测量法予以剔除[12]。磁通门磁强计在磁场强度为0的环境下会存在一个偏差，其补偿值在卫星发射之前应进行校正[11]；但在卫星发射升空之后，磁强计的零位补偿值会因为电子器件温度变化或老化等因素而发生缓慢改变，所以需要对该补偿值进行在轨标定。

空间环境中存在着大量的磁流体力学波动[13-14]，其中磁场压缩波动会改变总磁场的强度，而剪切阿尔芬波动不会改变总磁场强度[15]。利用阿尔芬波动的这一特性，基于所选时段的行星际空间磁场波动是阿尔芬波动的假设，Belcher方法[16]、Hedgecock方法[17]和Davis-Smith方法[18]等获取磁通门磁强计零位补偿的方法被提出。其中，Davis-Smith方法是使磁场幅度平方的方差最小化，被认为是目前深空探测中磁强计在轨标定的最优方法[19]。

行星际空间中存在大量磁场波动，但没有纯的阿尔芬波动[19]。为确保Davis-Smith方法计算零位补偿的可靠性，需要筛选出阿尔芬特性足够好的行星际磁场数据时段。为此，Leinweber等人[19]对数据窗口的筛选提出了3个准则：1）磁场剪切扰动需要绕多个非平行轴有显著的旋转；2）磁场压缩扰动整体上处于较低的水平；3）磁场矢量中的任一分量与总磁场的平方满足较强的线性关系。其中，磁场压缩扰动大小的控制采用的是经验值。

近期的研究表明，磁场波动的频率和幅度等对采用Davis-Smith方法计算磁强计零位补偿的误差有显著影响[20-21]。本文通过数值仿真研究在不同频率和幅度下的剪切阿尔芬波动对采用Davis-Smith方法计算磁通门磁强计零位补偿误差的影响，给出磁场压缩扰动处于较低水平的参考值，以期提高深空探测中磁通门磁强计的在轨标定精度。

1 Davis-Smith 方程

采用相关性分析可推导出Davis-Smith方程[19]。在数学上，若变量x和y是独立的，即x和y不相关，则其协方差Sxy= 〈xy〉-〈x〉〈y〉=0。设BM=(B1,B2,B3)为磁强计测量到的磁场，BA=(BA1,BA2,BA3)为自然磁场，O=(O1,O2,O3)为零位补偿，则有：

不论阿尔芬波动中的磁场扰动幅度有多大，其总磁场强度是不变的，即磁场各分量（BA1、BA2或BA3）与总磁场强度的平方（|BA|2）都不相关，于是有：

将式(1)代入方程(2)～(4)之后，将磁补偿放置于其中一边，可得：

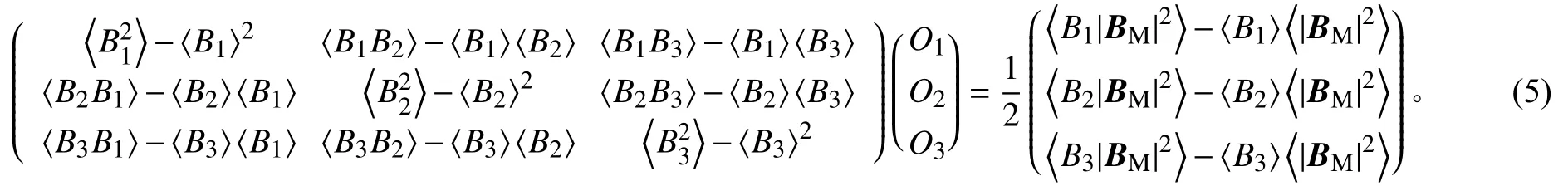
方程(5)左边是一个协方差矩阵，它与磁补偿O之间是相互独立的。将减去各自的平均值后记为，于是有

2 数值仿真

如果磁通门磁强计所测磁场BM为自然磁场，那么磁强计的真实零位补偿值为0；此时将所测磁场BM代入Davis-Smith方程后计算出来的结果即为磁强计零位补偿的误差。本文采用数值仿真分析，设定好磁场BM的时间序列后，代入到Davis-Smith方程分析磁场压缩扰动的相对幅度对磁强计零位补偿误差的影响。

2.1 单频波动

近期的研究结果表明，如果在数据窗口中磁场压缩波动的周期和剪切阿尔芬波动的周期相同，则阿尔芬波动的相关参数（如周期和幅度）会对Davis-Smith方程计算磁通门磁强计的零位偏移量的精确度产生显著影响[21]。首先分析剪切磁场波动只出现在x和y分量上的情况，并引入一个小幅度的磁场压缩波动。设定磁场x、y分量和总磁场的剪切波动为：

其中：A为磁场剪切波动的幅度；ωc为压缩波动的角频率，取ωc=0.105 rad/s（或周期TA=1 min）。数据分辨率为1 s，数据窗口时间长度为10TA。

将上述磁场代入Davis-Smith方程后，计算得到磁强计零位补偿的误差如图1所示，其中ΔO1、ΔO2和ΔO3分别代表Bx、By和Bz分量的零位补偿误差，A以步长 0.1 nT 从 0.5 nT 增加到 8 nT。可以看到，ΔO3的幅度比ΔO1和ΔO2的大了约1个数量级。对于方程(7)～(9)所设置的波动而言，即使磁场压缩波动的幅度很小，磁场的零位补偿误差也是非常显著的；当A=1 nT时，ΔO1和ΔO2的值都大于 50 nT；当A=2 nT时，磁场 3个分量的补偿误差值显著减小，ΔO1、ΔO2和ΔO3均随着A的增加而减小并趋于0。行星际空间中的磁场强度典型值在10 nT附近，而图1中的零位补偿误差最大可达到几十至几百nT。近期的研究表明，当压缩波动的周期和剪切波动周期相同且是单频波动的情况下，零位补偿的计算会出现显著误差，特别是在压缩波动占主导的磁场分量上[21]。该研究结果可解释图1中出现的显著的零位补偿误差值。

图1 Davis-Smith方程计算出的零位补偿误差与阿尔芬波动幅度的关系Fig.1 The relation between the magnetometer offset and the amplitude of the Alfvén wave based on Davis-Smith method

2.2 Bx包含与压缩波相同频率的波动

由图1可见，当阿尔芬波动为单频波动且周期和磁场压缩波动相同时，由Davis-Smith方程计算出的磁强计零位补偿误差非常显著。为了减小该误差，在方程中引入多个不同周期的磁场扰动，并使总磁场扰动与方程(9)保持一致，设定磁场x、y分量和总磁场随时间的变化为：

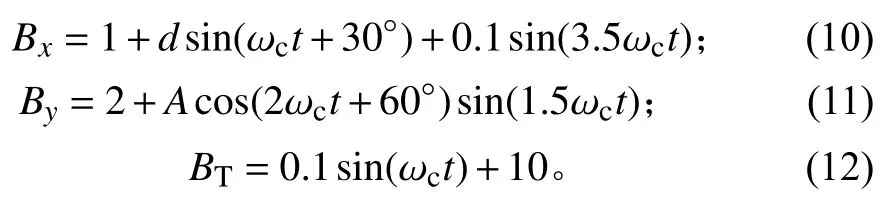
其中参数d用于控制Bx分量中和压缩波动频率相同的磁场波动的幅度。在式(10)、(11)中所引入的其他频率的磁场波动的参数具有一定的随机性，但这便于分析各分量磁场波动相对压缩波动的幅度对零位补偿误差的影响。

为量化磁场各个分量的波动幅度，定义数据窗口中各磁场分量的平均波动幅度为该磁场分量的标准偏差。的值用于描述磁场波动的总平均波动幅度SA，其中SBx、SBy和SBz分别为磁场x、y和z分量的平均波动幅度。总磁场BT的标准偏差SBT可视为压缩波动的平均波动幅度。行星际空间中不存在纯的剪切阿尔芬波动，并且很难将阿尔芬波动和压缩波动严格地从磁场扰动中分离出来。因此，定义R=SA/SBT为磁场波动与压缩波动平均波幅度之比，R值越大则表明阿尔芬波动的相对幅度越大。当参数d=0.1 nT时，将磁场剪切波动幅度A从初值0.1 nT开始按步长0.1 nT增加；A每改变1次，都将磁场各分量Bx、By和Bz代入Davis-Smith方程中计算出其零位补偿误差，它们随R值的变化如图2所示。由图可见：By和Bz分量的零位补偿误差ΔO2和ΔO3随着R值的增加而减小，并逐渐趋于0。在R=5时，ΔO2和ΔO3减小得最快；当R＞10时，ΔO2和 ΔO3减小至 0.5 nT 以下，且减小的趋势趋于缓和；同时，Bx的零位补偿误差ΔO1随着R值的增加呈现出先快速增加至约3 nT，然后缓慢减小至2.5 nT的走势。

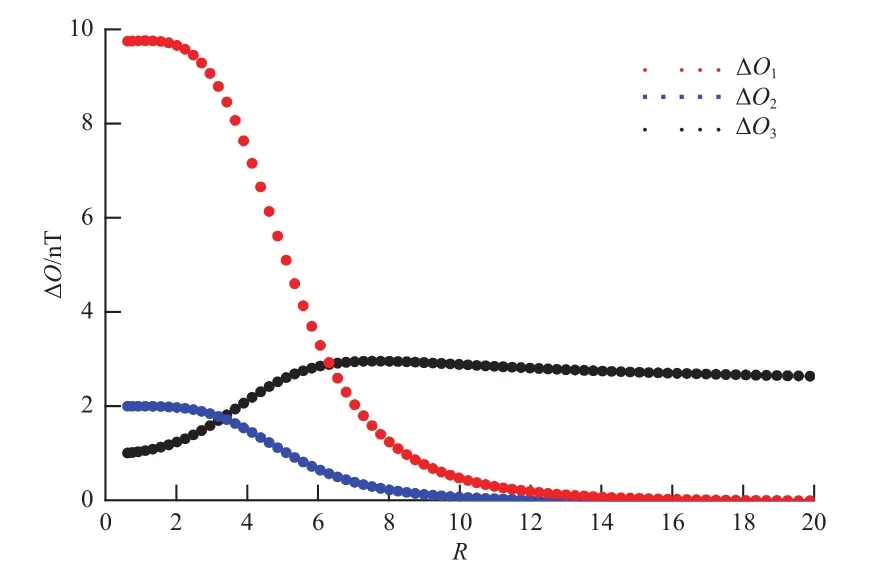
图2 Bx包含与压缩波相同频率的波动时，磁场3个分量的零位补偿误差随R值的变化关系（d=0.1 nT）Fig.2 The relation between the error of the magnetometer offset and the relative wave amplitudeRwhen theBx fluctuations contain the same frequency as the compressional wave (d=0.1 nT)

将方程(10)～(12)中参数d的值增加到1 nT后，采用和图2相同的处理方法，获得磁场3个分量的零位补偿误差如图3所示。对比图2和图3可见：由于参数d值的增加，图3中R的起点明显比图2中的大；By和Bz分量的零位补偿误差ΔO2和ΔO3的大小和变化趋势和图2中的基本一致；Bx分量的零位补偿误差ΔO1明显比图2中的小，且图3中的ΔO1随R值的增加缓慢减小并趋于0.5 nT。由此说明，当增加Bx分量中和压缩波动频率相同的波动的幅度时，可减小该磁场分量的零位补偿误差。此外，当R值增加到10时，磁场3个分量的零位补偿误差已显著减小。

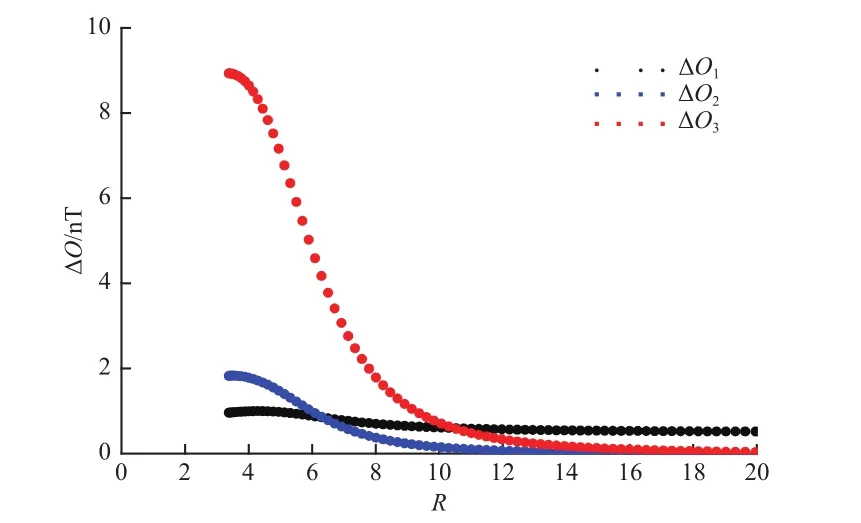
图3 Bx包含与压缩波相同频率的波动时，磁场3个分量的零位补偿误差随R值的变化关系（d=1 nT）Fig.3 The relation between the error of the magnetometer offset and the relative wave amplitudeRwhen theBxfluctuations contain the same frequency as the compressional wave (d=1 nT)

2.3 Bx和By中不包含与压缩波相同频率的波动

接下来，设定Bx和By分量中不包含与压缩波动相同频率的波动，并设置磁场x、y分量和总磁场随时间的变化为：

图4所示为d=0.1 nT时磁场3分量的零位补偿误差随R值的变化关系。由图可见：磁场3个分量的零位补偿误差都呈现出随着R值增大而减小并趋于0的趋势，Bz分量的零位补偿误差ΔO3明显比另外2个分量的补偿误差ΔO1和ΔO2大，这可能与该分量包含了与压缩波动频率相同的波动有关；在R=5附近，磁场3个分量的零位补偿误差衰减速度最快；在R=10附近，各分量的零位补偿误差在0.5 nT附近或小于0.5 nT，减小趋势也趋于缓和。

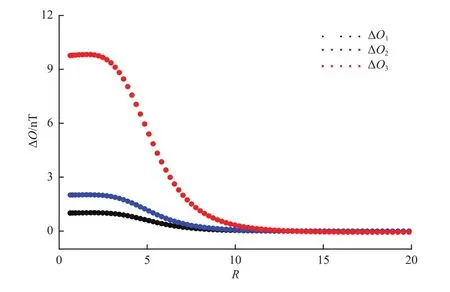
图4 Bx和By中不包含与压缩波相同频率的波动时，磁场3个分量的零位补偿误差随R值的变化关系（d=0.1 nT）Fig.4 The relation between the error of the magnetometer offset and the relative wave amplitudeRwhen theBxandByfluctuations do not contain the same frequency as the compressional wave (d=0.1 nT)

为考察Bx分量幅度对零位补偿误差的影响，取d=1 nT时零位补偿误差随R值的变化关系如图5所示。对比图4和图5可见：图5中各分量的零位补偿误差变化趋势和图4中的是一致的；当R＞7时，图5中各分量的零位补偿误差大小和图4中的近似相等；在R=10附近，各分量的零位补偿误差值都在0.5 nT附近或小于0.5 nT，其变化趋势也趋于缓和。

图5 Bx和By中不包含与压缩波相同频率的波动时，磁场3个分量的零位补偿误差随R值的变化关系（d=1 nT）Fig.5 The relation between the error of the magnetometer offset and the relative wave amplitudeRwhen theBxandByfluctuations do not contain the same frequency as the compressional wave (d=1 nT)

3 结论

本文通过数值仿真分析了在不同的磁场波动频率和幅度条件下用Davis-Smith方法计算磁强计零位补偿的误差变化趋势。主要结论如下：

1）若数据窗口中的磁场波动为单频波动，且其频率与压缩波动频率相同，则零位补偿误差非常显著；当数据窗口中的磁场波动为宽频波动时，如果某一磁场分量包含与压缩波动频率相同的波动，则该分量的零位补偿误差值会相对较大。

2）磁场各分量的零位补偿误差随着总磁场相对平均波动幅度R的增加而趋于减小；当R=5～10时，零位补偿误差的减小幅度最快；在R＞10时，零位补偿误差已显著减小，且变化趋势也趋于缓和。

以上仿真结果表明，在对深空探测卫星的磁通门磁强计进行在轨标定时，应选择幅度较大的宽频阿尔芬波动；而压缩波动的频率尽可能是窄带的。本文建议磁场压缩扰动处于较低水平的参考值为R=5～10，且R值越大，零位补偿误差越小。