组合导航中磁强计干扰估计与补偿方法
曾 成,李文霄
(1.河北工业大学 电子信息工程学院,天津 300401;2.天津市电子材料与器件重点实验室,天津 300401)
0 引言
三轴磁强计具有体积小、质量轻、功耗低的优点,被广泛用于导航、航空磁测、卫星定姿等领域[1]。在组合导航定位中,三轴磁强计作为敏感器件用来测量磁场的大小和方向,常与陀螺仪结合使用约束航向角误差。但因其器件特性,受自身误差和外界干扰的影响较大,导致航向角偏差较大[2]。航向角偏差严重时会导致重大事故发生,造成不可预计的后果。因此在设备使用过程中需要对三轴磁强计进行误差与干扰的估计,并对其进行补偿,从而使航向角更加精准[3-4]。
目前,三轴磁强计误差补偿常用方法有极大极小值法、椭球拟合校正法和矢量点积不变法。文献[5]提出一种极大极小值校正方法,能校正灵敏度误差和零偏误差,但补偿后航向角的精度偏低。文献[6]提出一种椭球拟合校正方法对三轴磁强计误差标定补偿,降低了计算量及磁强计误差,提高了航向角精度。文献[7]针对外界磁场对椭球拟合的影响,在补偿中采用分段优化,进一步提高了航向角精度。但椭球拟合需要本地地磁信息的准确值且要采集大量不同姿态下磁场矢量数据,过程复杂、不易实现。文献[8-9]采用一种矢量点积不变性校正方法,无需本地地磁场精确数据,可实现三轴磁强计的坐标系对准。但该方法辅助矢量的选取仍然难以实现。
针对三轴磁强计误差补偿常用方法中补偿精度较低、过程复杂和辅助矢量较难选取等缺点,在组合导航中,常利用多种传感器相结合的方法对磁强计误差校正。文献[10]提出磁强计与加速度计相结合的方法,利用极大极小值对磁强计初步校正,再利用矢量点积不变性对磁强计进一步校正。但该方法需保证处于零速区间,并且算法复杂。文献[11]将3种测量仪器优势互补,利用陀螺仪作为估计值预测姿态角,加速度计和磁强计的数据作为观测值进行修正,从而解算出高精度的姿态数据。但该方法在磁强计受到较大干扰时,未进行干扰补偿,导致此种情况下磁强计误差过大,航向角的精度明显下降。
本文利用陀螺仪短时精度较好、长期误差较大,而磁强计本身器件误差较大、长期误差较小的特点,提出一种磁强计的磁场干扰补偿方法。利用磁强计受干扰情况下陀螺仪在卡尔曼滤波算法中可信度较高的条件,建立磁强计的干扰模型。将磁强计的三轴磁场干扰转化为水平面上的两轴磁场干扰并对其进行估计,从而补偿磁强计的输出值,提高航向角精度。该方法无需采集大量不同姿态下的磁场信息,方法简单,实时性强,适用于磁场干扰较大的场景。
1 磁强计输出模型
磁强计的输出主要受自身误差影响和外界磁场的软硬磁干扰影响[12],可建立磁强计输出模型为
B′=K·B+b,
(1)
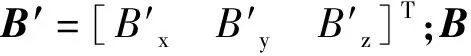
补偿后磁强计的输出为
B=K-1·(B′-b),
(2)
本文方法针对磁场干扰即矢量b进行求解,对磁强计进行补偿为
B=B′-b。
(3)
2 磁强计干扰补偿方法
在文献[11]提出的卡尔曼滤波算法中,当磁强计受到干扰时,其解算出的航向角失去准确性,此时陀螺仪可信度较高。而在无磁场干扰情况下,磁强计解算的航向角角度差与陀螺仪解算的航向角角度差相等。将磁强计三轴输出量通过陀螺仪解算的横滚角与俯仰角转化为水平面上的两轴输出量,建立干扰影响后磁强计的输出模型,并对干扰进行估计与补偿,并求解补偿后的航向角。
2.1 三轴磁强计解算航向角
三轴磁强计的坐标系与载体坐标系重合。三轴磁强计的x轴沿载体纵轴向前,y轴沿载体横轴向右,z轴与两水平轴垂直,方向向下。通过三轴磁强计测量地磁矢量,当三轴磁强计处于水平状态时,可通过三轴磁强计的两水平磁轴的测量值计算载体的航向角[13]。磁强计在导航中的测量原理如图1所示。
图1 三轴磁强计的测量原理图
Fig.1 The measuring principle of three-axis magnetometer
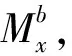
(4)
由于地球的自转轴和磁轴不完全重合,故地磁的北向和地理的北向之间存在一个磁偏角α。将磁偏角补偿到航向角ψ中,可求得航向角ψm为
(5)
2.2 陀螺仪解算航向角
与磁强计解算航向角的方法不同,陀螺仪利用四元数原理和四阶龙格-库塔算法对姿态角进行解算,导航坐标系相对于陀螺仪载体坐标系的转动四元数为[14-15]
Q=q0+q1i+q2j+q3k,
(6)
利用转动四元数表示捷联矩阵为
(7)
根据式(7)求解横滚角θ、俯仰角γ、航向角ψ为
(8)
根据四元数的相关理论[16],得到转动四元数的微分方程为
(9)
式中,⊗表示四元数乘法,ω=0+ωxi+ωyj+ωzk,ωx、ωy和ωz分别为陀螺仪输出的三轴角速度。
微分方程式(9)的矩阵形式为
(10)
利用四阶龙格库塔法解四元数微分方程式(10),通过式(11)实现四元数实时更新:
(11)
式中,h=tk+1-tk,为四元数的更新周期。
将四元数代入式(7),得到捷联矩阵,再根据式(8)即可得到由陀螺仪解算的3个姿态角,其中ψ为所求航向角。
2.3 磁场干扰估计与补偿方法
通过2.2节中陀螺仪解算的横滚角和俯仰角,对磁强计的三轴分量进行转换,获得磁强计在水平面的投影Mx,My为
(12)
根据式(12)得到磁强计解算的航向角公式为
(13)
令ψt1和ψt2分别为陀螺仪在t1和t2两个时刻解算的航向角,ψm1和ψm2分别为磁强计在无干扰情况下在t1和t2两个时刻解算的航向角。为保证航向角变化足够大,采取时间间隔为t,进行数据采集。根据陀螺仪与磁强计解算出的航向角差值相同,建立等式如下:
tan(ψt 2-ψt1)=tan(ψm2-ψm1),
(14)
tan(ψt 2-ψt1)可以通过陀螺仪进行求解,令A=tan(ψt 2-ψt1),由式(13)和式(14)可得
(15)

(16)
将式(16)化简可得
(17)
式中
k1=M1y-M2y-AM2x-AM1x,
k2=M2x-M1x-AM2y-AM1y。
将式(17)转化为
F=k1b′x+k2b′y+k3-R。
(18)
当样本点超过3个(耗时超过3 s)时,利用最小二乘拟合法使F最小,求出磁强计的两轴磁场干扰b′x、b′y。根据式(3)可知两轴干扰补偿与三轴干扰补偿原理相同。对磁强计进行两轴补偿,得到补偿后的磁场强度,再利用补偿后的数据对航向角进行解算。
3 磁场干扰的估计与补偿步骤
对磁场干扰估计与补偿流程如图2所示。
第一步,输入t时刻陀螺仪与磁强计原始数据以及t-1时刻陀螺仪解算的航向角;
第二步,根据式(8)对陀螺仪的数据进行航向角、横滚角与俯仰角解算;
第三步,将第二步中解算的航向角与t-1时刻的航向角作差并根据式(12)将磁强计的三轴分量转化为两轴分量;
第四步,利用两个时刻航向角的差值,每隔1 s进行一次计算,并将解算的差值与磁强计两轴分量代入到干扰模型式(18)中;
第五步,利用最小二乘法对干扰求解,并对磁强计进行补偿,根据式(13)求解经干扰补偿后的航向角。
图2 干扰补偿方法流程图
Fig2 Flow chart of the interference compensation
4 实验分析
实验采用低成本MEMS传感器 MPU9250,该传感器包含三轴磁强计、三轴陀螺仪和三轴加速度计三类传感器。并在高精度转台上进行验证。高精度转台与传感器的固定如图3所示。
实验选取在磁场干扰较大的室内,当地地磁强度为B=53.934 μT。实验分为两步采集数据。第一步,将mpu9250传感器固定在高精度转台上,采样率设定为100 Hz。在转台边放置磁场干扰源,对传感器通电后开启转台,令转台分别水平转动两周和竖直转动一周,采集磁强计的数据。第二步,任意转动传感器采集数据,采集20 s的数据用来验证校正效果。由于椭球拟合法需采集大量不同姿态下的磁场信息,矢量点积不变法需获取静止区间的重力矢量,两种方法步骤复杂,实时性差,不适用于磁场干扰较大的场景。因此,分别利用文献[5]中极大极小值法和本文方法对采集数据进行解算,补偿磁强计。实验通过比较磁场强度的最大最小绝对误差和均方根误差以及陀螺仪解算出的航向角验证补偿效果。
图3 高精度转台与传感器的固定图
Fig3 High precision turntable and installation of sensors
通过上述实验进行数据采集,并与当地地磁强度对比,误差结果如图4所示,磁强计未经补偿前测得的地磁场强度值的最大最小绝对值误差为43.622 μT,均方值误差为17.248 μT,磁场干扰对磁强计的作用较大。经文献[5]所述的极大极小值法补偿后,磁强计最大最小误差降到至14.731 μT,均方误差降至7.416 μT,说明极大极小值法对受到干扰后的磁强计补偿的效果不理想。
图4 未校正的磁强计误差图
Fig.4 Error of uncorrected magnetometer
根据图5可知,经过干扰补偿方法后,磁强计的最大最小绝对值误差降至0.499 μT,均方误差降至0.519 μT,比极大极小值法提高了6.897 μT,有效去除了干扰对磁强计的影响。
图5 两种方法补偿后磁强计误差的对比
Fig.5 Comparison of magnetometer errors corrected by two methods
图6和图7进一步展示了补偿算法对磁强计的补偿效果。由于未补偿干扰前磁强计的误差较大,导致磁强计解算的航向角与陀螺仪解算的差值也较大,航向角变化角度仅为50°到150°左右,而补偿后的磁强计解算出的航向角大致与陀螺仪解算出的航向角相似,可以看出磁强计干扰补偿方法是一种有效的磁强计干扰补偿方法,提高了磁强计解算航向角的精度。
图6 磁强计未补偿前的航向角的对比
Fig.6 Comparison of heading angle before uncompensated magnetometer
5 结论
本文针对组合导航定位中磁场干扰较大导致磁强计解算航向角严重失准的问题,利用陀螺仪与无干扰时磁强计解算的航向角角度差相吻合的特点,提出一种磁强计干扰补偿方法。通过建立干扰模型并采用最小二乘拟合法估计磁场干扰值,用来补偿磁强计的输出,提高航向角精度。实验结果表明,该方法运算简单,无需大量采集不同姿态的数据,补偿后磁场强度的绝对误差降至0.499 μT,均方根误差降至0.519 μT,有效提高了航向角准确度,补偿效果明显,适用于磁场干扰场景。
图7 磁场干扰补偿后磁强计航向角的对比
Fig.7 Comparison of heading angle corrected by interference compensation

