基于多智能体的电动汽车滑移率控制方法
张袅娜,张晓芳
(长春工业大学 电气与电子工程学院,吉林 长春 130012)
0 引言
在电动汽车安全行驶过程中,制动稳定性是非常重要的一部分,而滑移率的控制直接影响电动汽车的制动稳定性。电动汽车制动滑移率控制为通过主动调节车轮力矩,确保车轮滑移率能维持在最优滑移率附近,使车轮获得较高的纵向附着力,防止车轮抱死现象的发生,从而提高汽车制动安全性。与传统汽车制动系统相比,电动汽车的执行部件是轮毂电机,其响应速度更快、执行效率更高,更加适合现代控制策略的应用[1]。滑移率控制的难点主要在于如何解决制动系统中的非线性和强不确定性问题[2]。Castro R D和Rui E A等[3]将一种防饱和条件积分滑模算法应用到滑移率的控制中,它根据期望转矩来估计附着系数的不确定性上界,从而提高了系统的鲁棒性和稳态精度,抑制了滑模控制系统中的抖振现象。但缺点是算法中使用的积分效应使系统中的动态性能降低。戴彦[4]提出了将模糊规则与滑模控制相结合的控制算法,对滑模控制中的切换项进行模糊化,使切换控制项在保证鲁棒性的前提下尽可能小,从而解决了制动系统滑模控制中的抖振问题。Castro R和Araujo R E等[5]提出将蓄电池SOC和机电复合响应带宽的影响考虑到滑移率的控制中,提出了一种鲁棒自适应控制算法,使得系统中的控制量由自适应项产出,提高了系统的响应速度。Yuan L和Zhao H等[6]将一种预测控制算法应用到电动汽车滑移率控制系统中,通过同时控制4个车轮的力矩,使4个车轮的滑移率维持在最佳滑移率附近,保证汽车在安全行驶的前提下,能够获得较大的驱动制动力,同时防止了电动汽车驱动时过度滑移与制动时车轮抱死情况的发生。
目前,计算机技术的蓬勃发展极大提高了复杂动态系统的发展速度。将智能体之间的协调配合应用到复杂的工作中,可大大提高工作效率与系统灵活性和鲁棒性[7]。因此,基于复杂系统的多智能体协调控制拥有着广阔的发展空间,目前国内外许多学者对多智能体系统进行长期和深入的研究。多智能体及其相关技术已经广泛应用于多电机控制、智能机器人、新能源电动汽车、分布式控制、计算机控制、交通控制、电子商务等多领域中[8-10]。伴随着电动汽车和多智能体的迅速发展,将多智能体技术应用到电动汽车的协调与控制中成为一个热点方向。
本文首先对电动汽车制动工况进行动力学分析,建立一个车轮的滑移率模型,然后将每个车轮及其控制器看成智能体,将多智能体理论应用于4个车轮的同步协调控制研究中,然后分别采用普通滑模和非奇异终端滑模对滑移率进行控制,并利用Lyapunov理论进行稳定性分析。最后,通过仿真软件MATLAB中的Simulink进行实验验证,验证了算法的有效性。
1 系统动力学分析
1.1 车辆制动系统模型
在电动汽车制动过程中,当不考虑轮胎与地面的滚动阻力和空气阻力,其受力情况如图1所示,可将运动方程表达为如下[11]:
车辆运动方程:
(1)
车轮运动方程:
(2)
车轮纵向摩擦力:
Fx=Nμ=μmg,
(3)
式中:m为1/4车体重量,v为车辆行进速度,Fx为车轮纵向摩擦力,N为车轮对地面的法向反力,μ为车轮与地面的附着系数,I为车轮转动惯量,ω为车轮角速度,R为车轮半径,Tb为制动力矩。
图1 车辆制动时动力学模型
Fig.1 Vehicle dynamic model under braking
电动汽车制动时会导致车速与车轮转速产生偏差,进而车轮与地面之间会产生滑移问题,滑移程度的大小用滑移率来表示[12]:

(4)
分别对λ求其一阶,二阶导数得

(5)
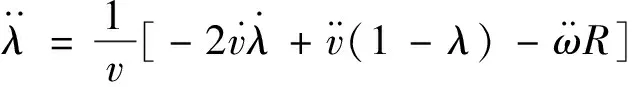
(6)
将式(2)、(3)代入式(5)、(6)中得

(7)
(8)
由式(1)和式(3)可得
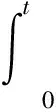
(9)
其中,v0为车辆制动时的初始速度。将式(9)代入式(8)中,并令
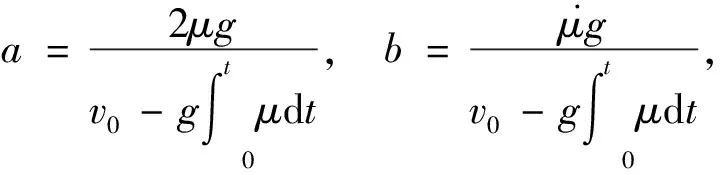
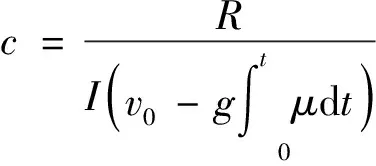
则式(8)可以写为
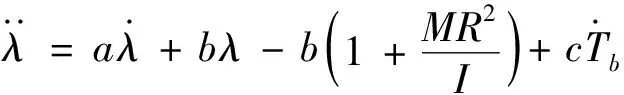
(10)
1.2 车轮轮胎模型
在不同的轮胎和路面附着条件下,轮胎的附着系数和滑移率之间的非线性关系曲线是不同的,轮胎的最大附着系数所对应的最优滑移率大小也不相同。在对最优滑移率的跟踪中,可采用通过已知轮胎模型的实验参数,经过推导计算来获得不同典型路面条件下的最优滑移率。
为了便于分析研究,本文采用的是结构简单实用的Burckhardt轮胎模型,通过模型参数来求取不同路面下的最优滑移率。Burckhardt轮胎模型具体表达式为[13]
μx=c1[1-e-c2λ]-c3λ,
(11)
其中c1,c2,c3为拟合系数,取值大小和具体的轮胎与路面附着条件有关。
由式(11)可分别求得路面最优滑移率和路面峰值附着系数为
本文选取6种常用标准路面作为对比道路,具体参数如表1。
表1 不同路面的最优滑移率及其附着系数
Tab.1 Optimal slip ratio of different pavements and its adhesion coefficient
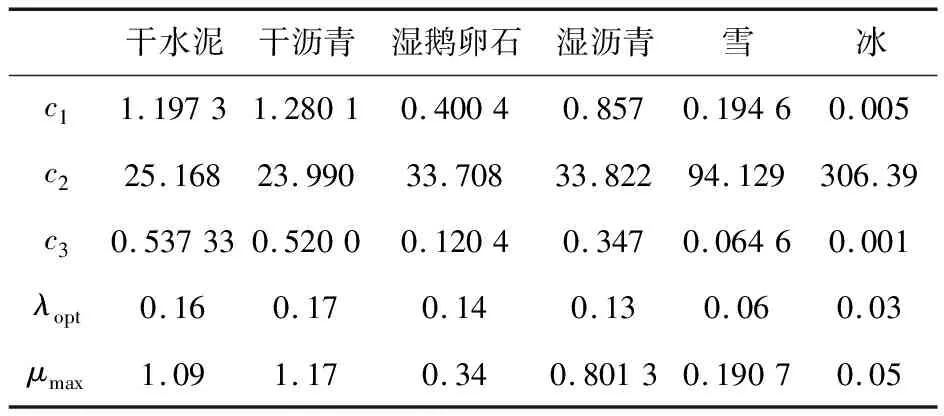
干水泥干沥青湿鹅卵石湿沥青雪冰c11.19731.28010.40040.8570.19460.005c225.16823.99033.70833.82294.129306.39c30.537330.52000.12040.3470.06460.001λopt0.160.170.140.130.060.03μmax1.091.170.340.80130.19070.05
2 控制算法研究
2.1 基于普通滑模的多智能体滑移率控制
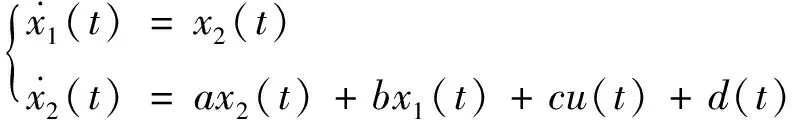
定义e1(t)=x1d-x1(t),e2(t)=x2d-x2(t)。
选取滑模变结构系统的滑模面为
s(t)=εe1+e2(t),
(12)
采用等速趋近率:
(13)
从而得出单个车轮的滑移率控制率为
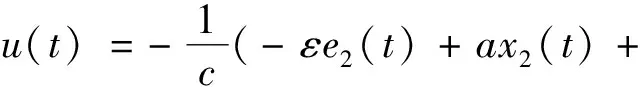
bx1(t)-ksgn(s(t)))。
(14)
由四轮轮毂电机电动汽车连接结构和内部工作原理可得多智能体系统的拓扑结构,如图2所示。设计智能体0为虚拟领导者智能体,4个车轮分别为智能体1,2,3,4。虚拟领导者智能体通过Burckhardt轮胎模型获得典型路面的最优滑移率,4个跟随者智能体跟踪领导者智能体的状态。
由多智能体的定义性质可得,系统相应的邻接矩阵A、入度矩阵D和拉普拉斯矩阵L分别为
图2 多智能体系统拓扑结构图
Fig.2 Multi agent system topology diagram
智能体i与领导者之间的连接权值用bi来表示,在这里假设,如果智能体i和领导者连通,则bi=1;否则,bi=0。由图2得B=diag(1,1,1,1)。

(15)
上式即为多智能体一致性控制协议,下面证明在该控制率下系统的稳定性。4个车轮分别跟踪虚拟领导者智能体运动,取:
,
(16)
将(15)和(16)代入(10)得4个车轮系统的表达式:
(17)
取矩阵M=L+B,则(17)可以表示为
(18)
K=diag(k1,k2,k3,k4),ε=diag(ε1,ε2,ε3,ε4),
证明系统稳定性,选取Lyapunov函数:
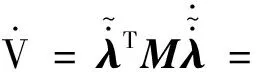
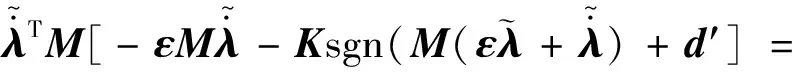

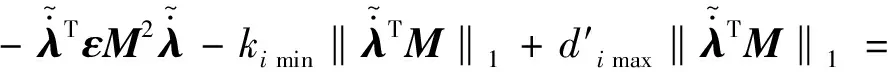
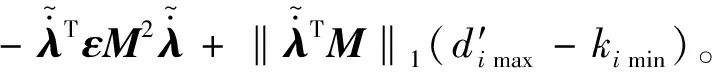
2.2 基于非奇异终端滑模的多智能体滑移率控制
考虑到普通滑模的有限时间收敛性和终端滑模的奇异性问题,本小节采用改进后的非奇异终端滑模控制算法进行制动滑移率控制。

(19)
i=1,2,3,4。
令控制率U=[u1u2u3u4]T,则误差动态方程可以表示为
(20)
其中,d代表不确定性及外部干扰,di≤lg。

(21)
其中,α=q/p,且奇数p,q满足1 (22) 可设计如下的控制率[14]: (23) 其中,η>0。 则滑模变量S能够在有限时间内到达滑模面S=0,达到系统的稳定。 其中: 即: 将(23)代入(20)得 由相轨迹特性可知,当ε2=0时,在有限时间内能够实现S=0。 在基于MATLAB的Simulink中搭建系统仿真模型,进行实验仿真。仿真参数:车轮滚动半径R=0.3 m,单轮车辆垂直载荷m=290 kg,(注意:前两个车轮的垂直载荷要大于后两个车轮垂直载荷),车辆转动惯量I=0.8 kg·m2,制动时车轮初始速度25 m/s。分别选取基于固定滑移率和干水泥路面两种工况条件下进行制动仿真实验。 车辆在基于固定滑移率工况下,车轮最优滑移率λd=0.2,对应路面最大附着系数μf=0.88;在此路面下的仿真结果如下: 采用普通滑模的多智能体算法和非奇异终端滑模的多智能体算法下的四个车轮滑移率仿真图如图3和图4所示。制动过程以左前轮为例,轮速和车速的仿真图如图5所示,两种算法下的制动距离如图6所示。 图3 普通滑模多智能体控制算法下的4个车轮滑移率 Fig.3 Slip rate of four wheels based on common sliding mode multi-agent control algorithms 图4 非奇异终端滑模多智能体控制算法下的4个车轮滑移率 Fig.4 Slip rate of four wheels based on nonsingular terminal sliding mode multi-agent control algorithms 图5 两种滑模多智能体控制算法下左前车轮的车身速度与车轮速度关系曲线 Fig.5 Relationship curve between body speed and wheel speed of left front wheel based on two sliding mode multi-agent control algorithms 图6 两种滑模多智能体控制算法下的车辆制动距离 Fig.6 Vehicle braking distance based on two sliding mode multi-agent control algorithms 由仿真分析图可知,两种基于多智能体的滑模算法都很好地满足了汽车的制动安全性。首先分析基于普通滑模的多智能体控制算法,由图3可得,电动汽车四个车轮的滑移率在t=0.5 s时都快速到达最佳滑移率附近,满足了电动汽车制动性能的要求,但4个车轮最后在约t=2.7 s时达到最优滑移率λd=0.2。以左前轮为例,由图5和图6可得电动汽车在约t=3.17 s,车速和轮速趋于零,汽车制动结束,制动距离约为39.7 m。分析基于非奇异终端滑模的多智能体控制算法,由图4可得,约在t=1.5 s时四个车轮的滑移率迅速一致地达到了最佳滑移率λd=0.2。同样以左前轮为例,由图5和图6可得,约在t=3 s车速和轮速趋于零,汽车制动结束,制动距离约为38.8 m。 选取车辆运行在干水泥路面情况下进行仿真实验,干水泥路面的最优滑移率为λd=0.16,路面最大附着系数为μf=1.09,在此路面下进行仿真实验的结果分析如下。 采用普通滑模的多智能体算法和非奇异终端滑模的多智能体算法下的四个车轮滑移率仿真图如图7和图8所示。制动过程以左前轮为例,轮速和车速的仿真图如图9所示,两种算法下的制动距离如图10所示。 图7 普通滑模多智能体控制算法下的4个车轮滑移率 Fig.7 Slip rate of four wheels based on common sliding mode multi-agent control algorithms 图8 非奇异终端滑模多智能体控制算法下的4个车轮滑移率 Fig.8 Slip rate of four wheels based on nonsingular terminal sliding mode multi-agent control algorithms 首先分析基于普通滑模多智能体滑移率控制算法,由图7可得,电动汽车四个车轮的滑移率在t=0.6 s时都快速到达最优滑移率附近,满足了电动汽车制动性能的要求。但4个车轮最后到约t=2 s时达到了最优滑移率λd=0.16。同样以左前轮为例,由图9和图10可得,电动汽车在大约t=2.445 s时车速和轮速都趋于0,汽车制动结束,制动距离约为31 m。分析在基于终端滑模的多智能体控制算法下,由图8可得,约在t=1.2 s时四个车轮滑移率都已达到了最优滑移率。以左前轮为例,由图9和图10可得,在约t=2.1 s时,电动汽车的车速和轮速都趋于0,汽车制动结束,制动距离约为28.5 m。 图9 两种滑模多智能体控制算法下左前车轮的车身速度与车轮速度关系曲线 Fig.9 Relationship curve between body speed and wheel speed of left front wheel based on two sliding mode multi-agent control algorithms 图10 两种滑模多智能体控制算法下的车辆制动距离 Fig.10 Vehicle braking distance based on two sliding mode multi-agent control algorithms 针对电动汽车制动过程中滑移率的控制是非线性、不确定性的时变系统,将多智能体理论和滑模控制算法相结合,并分别设计了基于普通滑模多智能体的控制策略和基于非奇异终端滑模多智能体的控制策略对电动汽车制动滑移率进行控制,最后选择车辆在标准均匀路面与干水泥路面两种路面工况下进行实验仿真。证明了本文提出的两种控制策略均能满足车辆制动稳定性的需求,其中基于非奇异终端滑模的多智能体控制策略效果更好些,使车辆的制动时间和制动距离更短。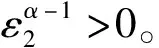
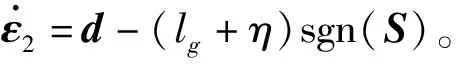
3 仿真研究
3.1 基于固定滑移率的多智能体算法控制仿真
3.2 基于干水泥路面的多智能体算法控制仿真
4 结论

