一类耦合Jansen-Rit模型中突变参数的非线性辨识
孙呈霞,吴向东,刘 仙,*
(1.燕山大学 电气工程学院,河北 秦皇岛 066004;2.北京理工大学 自动化学院,北京 100081)
0 引言
由于直接记录的脑节律可能会因为神经元和放大器中的噪声干扰以及记录装置中的不确定性而变得不准确,所以状态估计和参数辨识在脑科学研究中起着十分重要的作用[1]。Deng等人[2]将无迹卡尔曼滤波器(Unscented Kalman Filter, UKF)算法与一种基于同步的方法相结合,从被噪声严重破坏的活动电位中估计出了FitzHugh-Nagumo模型和Hidmarsh-Rose模型的所有未知参数。Liu等人[3]和Shan等人[4]证明,UKF也可以有效估计神经群模型的不可测状态以及参数。Lankarany等人[5]提出双扩展卡尔曼滤波器算法和双无迹卡尔曼滤波器算法来重构Hodgkin-Huxley模型的动力学,并通过记录的噪声干扰下的膜电压数据辨识出了模型的未知参数。随后,Liao等人[6]证实,容积卡尔曼滤波器(Cubature Kalman Filter, CKF)及其改进滤波算法可以用于估计Hodgkin-Huxley模型的状态和辨识模型的参数,并且统计结果表明双容积卡尔曼滤波器方法的辨识精度更高。Armando等人[7]发现CKF也适用于估计癫痫持续状态下的一类神经群模型的状态和参数。
如上所述,在神经科学领域,大部分用于辨识参数和估计状态的方法是基于模型提出的,所以数学模型的选择也是一个关键点。完善的数学模型可以准确地模拟真实的脑节律,这是我们研究辨识和估计方法的前提[8-9]。目前用于模拟脑电图(Electroencephalogram, EEG)信号的模型主要有两大类。一类是从微观层面上模拟单个神经元的活动,如前面提到的FitzHugh-Nagumo模型[10]、Hidmarsh-Rose模型[11]和Hodgkin-Huxley模型[12]。大脑不同区域的信息往往要通过耦合许多神经元模型来模拟。这种建模方式的缺点是它需要很强的计算能力来求解模拟状态。另一类是从宏观层面上模拟大量神经元的平均活动,例如神经群模型[13-14]。类似于Jansen-Rit模型这样的宏观神经群模型既简单又更具生理意义,是神经科学研究中最常用的模型。之前提到的那些卡尔曼滤波方法在神经科学领域的局限性在于它们无法有效辨识突变参数。已有研究指出,脑功能障碍可能是由于大脑系统内部参数之间的平衡关系被破坏而引起的内部失稳所致[15-16]。当局部参数突然发生变化且超出了系统的自我调整范畴时,该区域可能会成为一个病灶源,产生的异常节律在耦合时延的作用下传播到其他区域,引发严重的神经疾病。因此突变参数的辨识对于神经疾病的预防和治疗来说意义重大。Li等人[17]利用强跟踪容积卡尔曼滤波器(Strong Tracking Cubature Kalman Filter, STCKF)来完成脉冲机动卫星系统中的实时估计和辨识任务。STCKF算法通过在状态误差协方差矩阵中引入渐消因子来调整卡尔曼增益矩阵,从而解决了非线性系统中突变参数的跟踪问题。STCKF为有效辨识脑系统中的突变参数创造了可能。
基于以上原因,本文尝试利用STCKF算法来估计一类耦合Jansen-Rit模型中的突变兴奋性增益参数。这项工作有望为脑部疾病病灶源的确定提供可能的方法。
1 Jansen-Rit模型
本文选用Jansen和Rit[18]建立的神经群模型作为基础模型来模拟实际脑活动背景下的不同节律。由于大多数实验数据(如由脑电图记录的EEG信号)反映的是大量神经元的集群活动,所以这类完全来源于现象学的宏观模型对于研究大脑机制等非常有效[19]。此外,与微观模型相比,这类模型对计算能力的要求不是很高。Jansen-Rit模型可以由8个一阶微分方程描述:
(1)
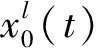
表1 模型参数的生理意义和标准值
Tab.1 Physiological meanings and standard values of the model parameters

参数生理意义标准值He平均兴奋性突触增益3.25mVHi平均抑制性突触增益22mVτe兴奋性膜平均时间常数与树突平均时延0.0108sτi抑制性膜平均时间常数与树突平均时延0.02sτd来源于某些群落的传出连接平均时延0.0303sC1主体细胞对兴奋反馈回路中中间神经元树突产生的平均突触连接数135C2中间神经元对兴奋反馈回路中主体细胞树突产生的平均突触连接数108C3主体细胞对抑制反馈回路中中间神经元树突产生的平均突触连接数33.75C4中间神经元对抑制反馈回路中主体细胞树突产生的平均突触连接数33.752e0最大点燃率5s-1v0对应于点燃率的突触后电位6mVrSigmoid变换的斜率0.56mV-1
已有研究表明,异常脑节律可能是某些神经群落中兴奋性参数He突然增大引发的,然后在耦合延迟的作用下棘波信号传播到其他群落。这表明,局部He的突然变化可能是脑功能障碍发生的根源。本文希望通过及时捕捉He的突然变化,为寻找病灶源提供一种可能的方法。
2 突变参数辨识方法
一类受到测量噪声干扰的离散非线性状态空间模型可以描述为[20]
(2)
其中,下标k表示采样时间点;xk∈RNx是采样时间点k处的状态向量,Nx表示该状态向量的维度;pk-1∈RNP是一个已知的随机输入,NP表示向量维度;yok∈RNy是测量向量,Ny表示向量维度;f(·):RNx+Nu→RNy和h(·):RNx→RNy分别表示非线性动力学函数和测量函数;wk表示测量噪声,服从均值为零方差为WK的高斯分布。
1)预测过程
该预测过程与CKF算法[22]的预测过程相同。具体描述为
(3)
其中上标*表示引入渐消因子和遗忘因子前的情况;Uk-1表示采样时间点k-1处的后验估计状态误差协方差矩阵Pk|k-1的乔利斯基分解因子;Chol(·)表示乔利斯基分解函数;φi为求容积点;ζ是一组标准正交点集,集合中的元素表示为
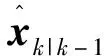
2)计算渐消因子λk
受强跟踪滤波器(Strong Tracking Filter, STF)算法[23]的启发,STCKF算法通过在CKF算法中引入渐消因子k和遗忘因子来提高对突变状态的跟踪能力。计算渐消因子λk的过程可以描述为
(4)
计算渐消因子λk:
(5)
其中,εk表示残差序列;yok和Wk与前文一致,分别表示测量向量和测量噪声的方差;Vk是一个与残差相关的中间函数;Nk和Mk是用于计算渐消因子λk的矩阵,而tr[Nk]和tr[Mk]分别为矩阵Nk和Mk的迹;ρ是残差序列的遗忘因子,并且0≤ρ≤1,通常取ρ=0.95;β为弱化因子,通常β≥1。
3)校正过程
该过程涉及到一个在计算出渐消因子λk之后重新计算先验估计状态误差协方差矩阵Pk|k-1的步骤:
(6)
校正过程的其余公式与CKF相同:
(7)
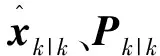
除了估计系统状态之外,CKF的另一个重要特性是,当与增广状态向量法[20]相结合时可以用于辨识未知参数,STCKF亦是如此。增广向量法通过将未知参数视为虚拟状态,把系统表达式改写为
(8)
其中qk∈RNq表示参数向量,状态向量由常数参数向量增广。在滤波器的更新作用下,即使没有相应的随机终止参数方程,辨识得到的参数向量qk仍会随时间变化。
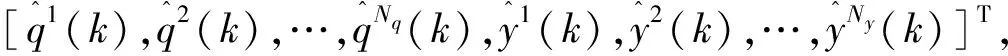
通过将衰减因子λk和遗忘因子ρ引入到CKF算法,来近似一个给定非线性系统的状态误差协方差矩阵,可以有效克服STF迭代过程中Jacobi矩阵的逼近精度低和计算繁琐的问题。同时,STCKF算法继承了STF对突变状态的强跟踪能力。
3 数值结果
本文利用一类3个节点耦合的Jansen-Rit模型来模拟真实的EEG信号,其连接结构如图1所示。这类模型中每个群落的数学表达如式(1)所示,其中N=3。受到测量噪声干扰的3个节点耦合的Jansen-Rit模型输出可以描述为
y(t)=h[x(t)]+w(t),
(9)
图1 3个节点耦合的Jansen-Rit模型的连接图
Fig.1 Connection diagram of a three-node coupled Jansen-Rit mode

第一组仿真实验中,群落1的兴奋性参数He的变化过程设置为3.6 mV→4 mV→3.4 mV→3.5 mV。在实际的脑系统中,引起脑疾病发作的局部参数突变可能不会像这样连续发生,而通常是从标准值变为一个非标准值。设置多次突变的目的是验证STCKF对突变参数的强跟踪性能。由于本文的主要目的是辨识突变参数,并且群落2和3的状态估计结果与群落1相似,本节只给出了群落1的相关结果。群落1的动力学特性如图2所示,可以看出模型输出的峰值和频率也会随着兴奋性增益值的变化而变化。
图2 第一组模拟实验中群落1的动力学
Fig.2 The dynamics of population 1 in the first set of simulation experiments
这里引入均方根误差(Root Mean Square Error,RMSE)[24]的概念来检验滤波算法的精度。计算第i个状态分量或局部参数的RMSE,公式为
(10)
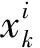
图3显示的是测量噪声影响下,经过CKF和STCKF的滤波处理后得到的输出估计和参数辨识结果,其中实线表示实际值,虚线表示输出估计结果,点划线表示参数辨识结果。图3(a)和(b)给出了两种滤波算法的输出估计结果,可以看出这两种滤波算法都可以准确估计群落1的输出。为了更直观地评价这两种滤波算法的精度,计算输出的RMSE值,得到R(y1)CKF=0.255 7和R(y1)STCKF=0.211 9,说明STCKF滤波算法的估计精度高于CKF。图3(c)和(d)给出了两种滤波算法的参数辨识结果,可以看出当辨识结果已经达到稳定状态时,CKF算法几乎失去对突变参数的跟踪能力,而STCKF算法能够讯速而准确地辨识出新的参数值。相关结果表明,STCKF算法不仅可以辨识出耦合Jansen-Rit模型中的突变兴奋性增益参数He,而且在估计精度方面优于CKF算法。
图3 第一组仿真实验得到的输出估计和参数辨识的结果
Fig.3 Output estimation and parameter identification results from the first set of simulation experiments
第二组仿真实验中,将群落1的兴奋性参数He的变化过程设置为3.25 mV→3.5 mV→3.25 mV→3.6 mV→3.25 mV→3.4 mV→3.25 mV。此时,群落1的动态特性如图4所示。图5是经CKF和STCKF算法处理后得到的输出估计和参数辨识结果。与图3一致,实线表示实际值,虚线表示输出估计结果,点划线表示参数辨识结果。计算得到R(y1)CKF=0.195 0以及R(y1)STCKF=0.174 1。因此,可以得出与第一组实验一致的结论。也进一步证明了STCKF算法在突变参数辨识和估计精度方面的优越性。
图4 第二组模拟实验中群落1的动力学
Fig.4 The dynamics of population 1 in the second set of simulation experiments
图5 第二组仿真实验得到的输出估计和参数辨识的结果
Fig.5 Output estimation and parameter identification results from the second set of simulation experiments
4 结论
本文针对耦合Jansen-Rit模型中参数突变的特点,给出了一种结合增广向量法的STCKF方法。该方法不仅可以估计模型的输出,也可以辨识模型中的突变参数。为了突出所给方法的优越性,将其与CKF方法进行比较。实验结果表明:1)CKF和STCKF算法都可以准确估计耦合Jansen-Rit模型的输出,并且通过计算输出的RMSE值,证明STCKF算法的估计精度高于CKF;2)CKF和STCKF算法都可以用于辨识一类耦合Jansen-Rit模型的参数,但是当参数突然变化时CKF算法几乎失去对参数的跟踪能力,而STCKF算法仍能够迅速而准确地辨识出发生了变化的参数值。本文工作有望成为进一步研究脑疾病抑制方法的良好开端。但是,仍有一些问题需要进一步探讨。例如,如何将这项研究与控制方案结合起来,以系统地减轻甚至消除神经疾病。这也是我们未来的工作重点。

