多点激励下大跨高低墩连续拱桥地震响应分析

连梦磊，杨德健，王清龙

（天津城建大学 土木工程学院，天津 300384）

近年来，西部大开发的大力发展，促进了西部山区交通的快速发展.公路、桥梁的大量修建给西部发展提供了必要的条件[1].由于西部多山区，沟谷，山区地形复杂，山高坡陡，修建跨越沟谷山头的桥梁成为首要解决的任务.因为这些桥梁要跨过河谷或深沟[2-4]，所以这些桥梁表现为上部结构一般为连续刚构或多跨连续梁的特点，而下部相邻桥墩墩高则相差悬殊[5].拱桥跨越能力较大，能充分做到就地取材，与梁式桥相比可以省大量的钢材和水泥，耐久性好，而且养护和维修费用少，因此在桥梁工程中得到越来越多的应用.地震现场的实测资料表明，即使在50 m的范围内，地基各点振动的幅值和相位也有很大差别[6].因此需要对存在墩高差的大跨桥梁进行多点激励和考虑墩高差的多点激励，以此来确保抗震设计的安全性.

1 多点激励运动方程

对于大型的空间结构，地震时地面各支撑点的运动不应视作相同的.一方面是由于行波效应所导致地面运动的多样性，另一方面是由于局部土壤的不同导致地震波中各种频率成分的含量不同，即局部场地效应.因此，地震方面的研究已不仅局限于结构的每个支座均承受相同地震激励影响，多点激励输入下的响应分析已成为结构抗震研究和工程设计需要考虑的热点问题.多点激励下，结构的内力不仅取决于相对位移，还与结构支座处地震动输入差异相关.

对一个自由度为n的线弹性离散结构体系，在有m个支点受到地面运动的非一致激励时，其运动方程可以写成矩阵形式，具体形式如下

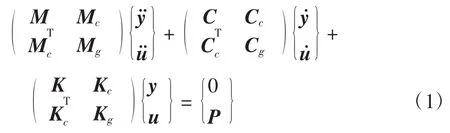
其中：M为结构非约束自由度的N×N维质量矩阵；C为结构非约束自由度的N×N维阻尼矩阵；K为结构非约束自由度的N×N维刚度矩阵；Mg为结构非约束自由度的m×m维质量矩阵；Cg为结构非约束自由度的m×m维阻尼矩阵；Kg为结构非约束自由度的m×m维刚度矩阵；Mc为M和Mg这两组自由度耦合的N×m维质量矩阵；Cc为C和Cg这两组自由度耦合的N×m维阻尼矩阵；Kc为K和Kg这两组自由度耦合的N×m维刚度矩阵；y¨、y˙、y 分别表示绝对坐标系下非支座节点的 N维绝对加速度、速度和位移列向量；u¨、u˙、u 分别表示绝对坐标系下支座节点的m维加速度、速度和位移列向量；P为m维支座反力列向量.

从运动方程（1）可以得到：My¨+Mcu¨+Cy˙+Ccu˙+Ky+Kcu=0，即

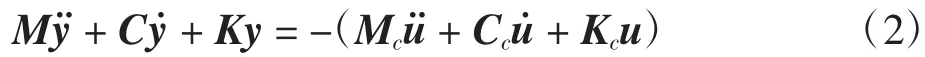
为了求解上式，将结构非支座节点处的绝对位移分为两部分，即

式中：ys为不考虑惯性力时由于地面运动所引起的拟静力位移向量；yd为结构由于惯性力所引起的动位移向量.

将方程（3）代入方程（2）中得

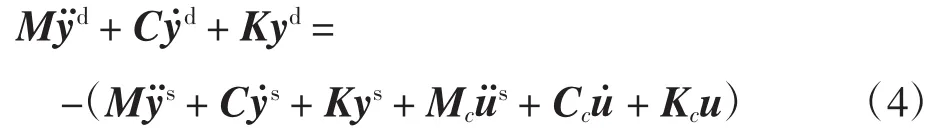
实际上，对于每个瞬间，Kys+Kcu=0，从而可以得到

其中：R=-K-1Kc称为影响矩阵.

将方程（5）代入方程（4）中，得

对于将质量理想化为集中在自由度处的结构，质量矩阵是对角阵，这意味着Mc为一个空矩阵，即Mc=0.且通常普遍认为，虽然速度项（即阻尼项）-（CR+Cc）u˙不为 0，但是与加速度项（即惯性项）-MRu¨相比，速度项很小，可以忽略不计.则方程（6）转化为

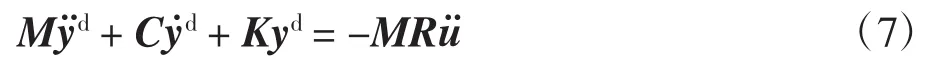
式（7）即求解结构地震响应的多点加速度输入模型.

2 高低墩桥梁模型概况

跨越山谷的桥梁往往两侧桥墩较低，中间桥墩较高，为详细研究高低墩桥梁在多点激励下的地震响应分析，建立了两个桥梁模型.模型一为2跨连续拱桥，桥墩固结，两侧桥墩高6 m，中间桥墩高19 m，墩高差13 m.跨径布置为25 m+100 m+100 m+25 m.桥梁模型正视图如图1所示.模型二除2号桥墩为19 m外，其余布置和模型一相同，桥梁模型正视图如图2所示.

运用abaqus软件建立桥梁有限元模型，两个桥梁模型梁单元均采用B32单元，小于500 mm的梁单元采用B31单元，桥面板单元采用S4R.结构自振周期采用的是特征向量法求解，动力方程求解方法采用的是直接积分法.

对于模型一和模型二各桥墩的土层参数如表1所示.

表1 土层参数

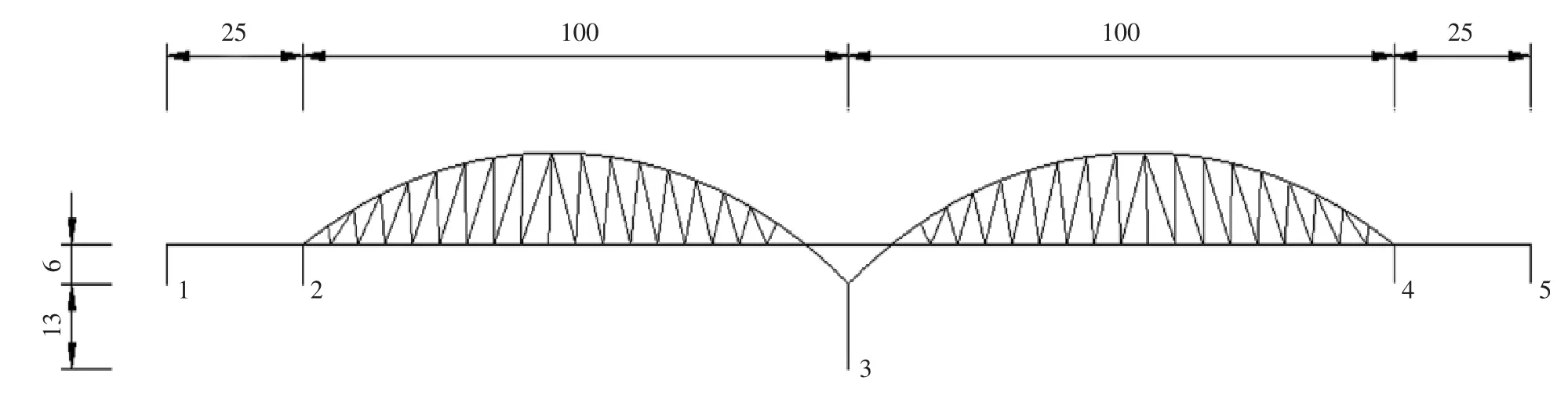
图1 桥梁模型1正视图（单位：m）

图2 桥梁模型2正视图（单位：m）

3 输入地震波分析

多点地震动输入是指在随机地震动合成时考虑地面的空间变化（如局部场地效应、行波效应以及相干效应等）的影响[7].该桥梁场地类型按Ⅱ，设防烈度按8（0.2 g），特征周期按0.25 s考虑.

（1）多点激励地震波.由目标反应谱拟合，通过目标功率谱[8]和相干函数[9]，生成只考虑多点激励的地震波.对于桥梁的影响，模型一和模型二在各点的地震波是相同的.根据人工生成地震波的原理，对幅值谱和相位差谱经快速傅里叶逆变换可以得到地震波的时程曲线[10].1至5点的地震波时程曲线如图3所示.

目标功率谱采用Clough-Penzien谱，水平地震波的迟滞相干函数选择Hao模型，拟合的规范反应谱分别依据现行公路桥梁规范生成目标场地多点地震动[11].1点和3点的实际功率谱和目标功率谱的拟合曲线如图4所示，从图中可以看出曲线拟合良好.

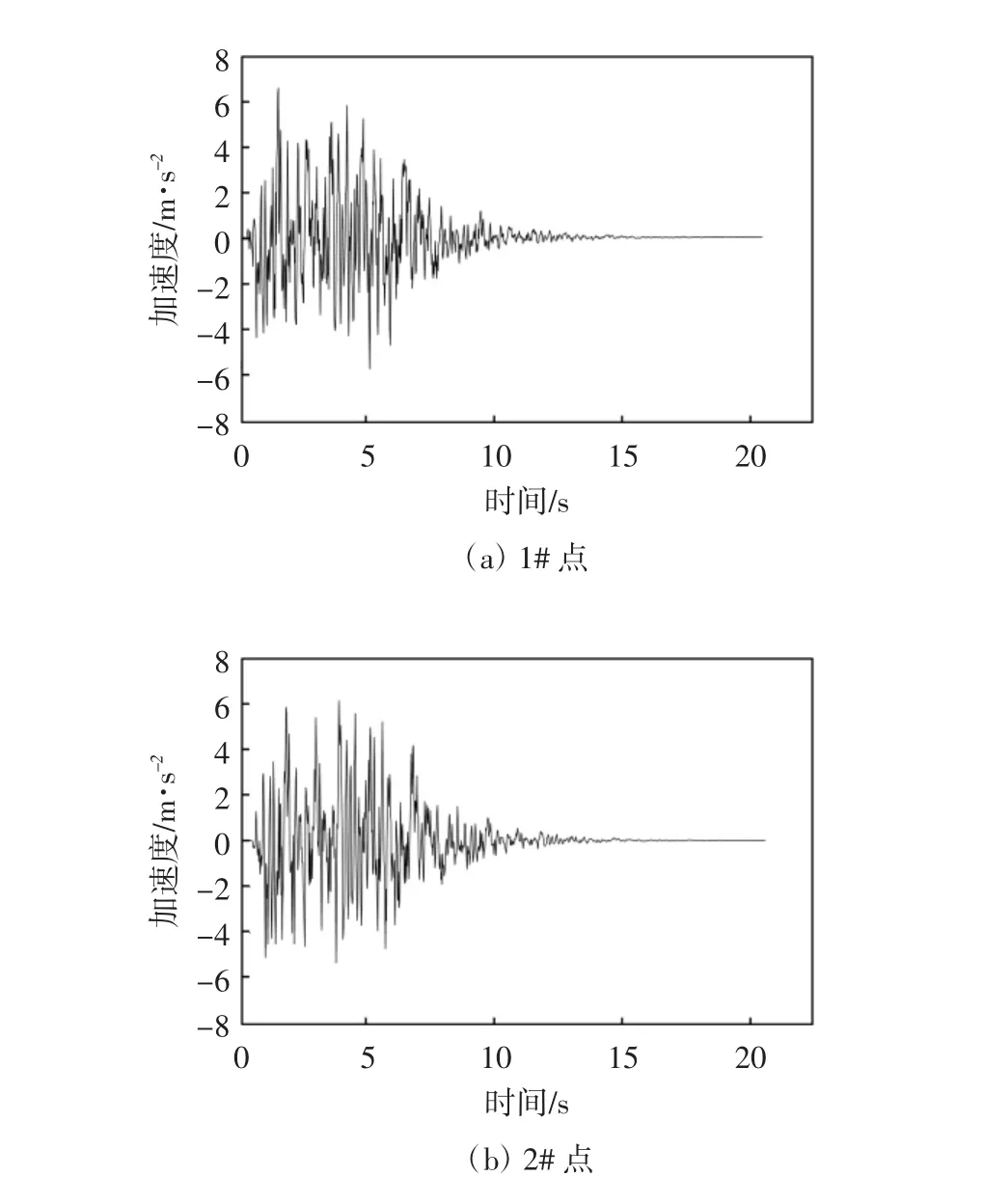
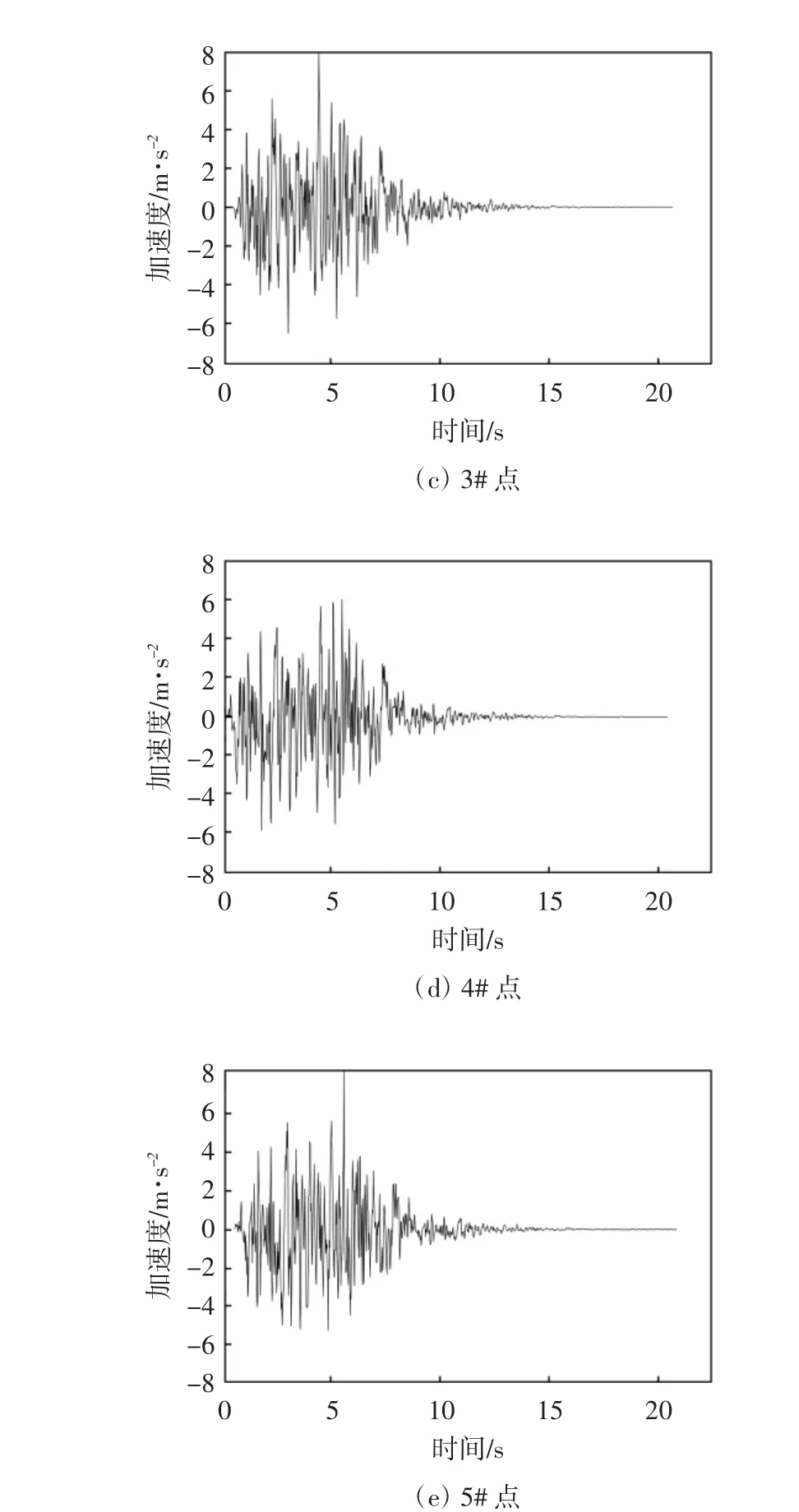
图3 地震动加速度时程曲线

（2）考虑墩高差的多点激励地震波.对于存在墩高差的桥梁，桥梁的墩高差对桥梁的抗震性能的影响主要由桥墩多处地层厚度及土层性质差异所致.文献[12]中结合多层土体的传递函数给出了地下地震动反应谱和功率谱模型的推导方法.结合地下多点地震动合成方法，利用文献[12]中求出的地下功率谱、反应谱和相干函数可得到考虑墩高差的地震波.

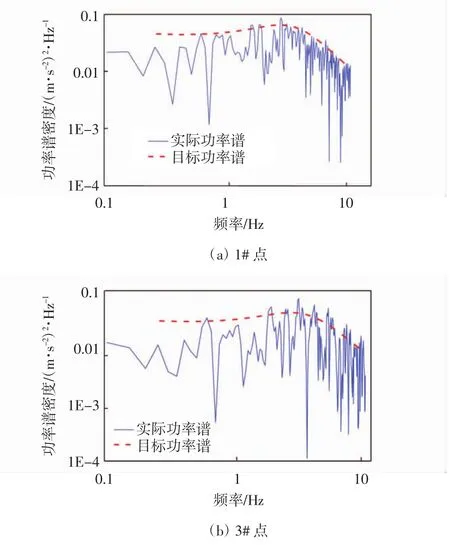
图4 实际功率谱和规范功率谱拟合曲线

对于模型一，桥墩3和各桥墩的墩底高度差为13 m，除3#点的地震波之外，其余各点地震动均与多点激励地震波一样，故仅介绍3#点地震波.考虑墩高差影响的3#点地震动时程曲线（见图5），图6画出了考虑墩高差影响的3#点实际功率谱和目标功率谱的拟合图，从图中可以看出曲线拟合良好.

对于模型二，桥墩2和桥墩3与各桥墩的墩底高度差为13 m，除2#点的地震波外，其余各点的地震波均与模型一在考虑墩高差时各点的地震波一样.图7给出了2#点的地震动加速度时程，考虑墩高差影响的2#点实际功率谱和目标功率谱以及实际反应谱和目标反应谱的拟合曲线良好.

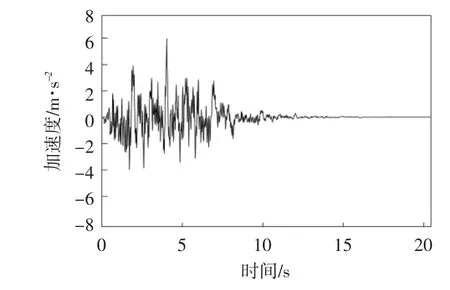
图5 3#点地震动加速度时程曲线

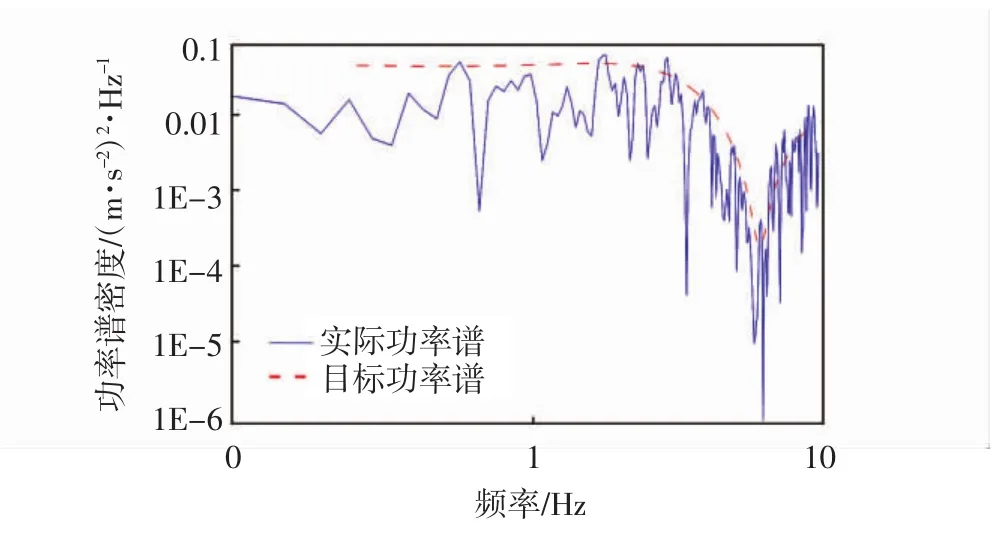
图6 3#点实际功率谱和规范功率谱拟合曲线

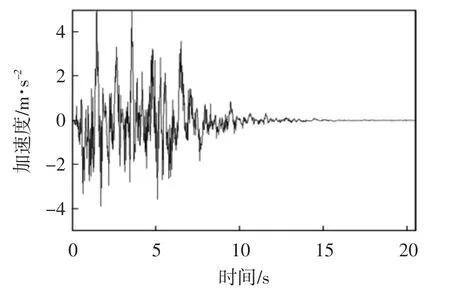
图7 模型二2#点地震动加速度时程曲线

综上所述，两种激励形式下的输入地震波其实际功率谱和反应谱均与所选择的目标函数之间拟合良好，因此这些输入地震波具有良好的实用性及可靠性.

4 不同激励方式下桥梁的时程分析与对比

连续拱桥在多点激励，考虑墩高差的多点激励下，各个桥墩墩底剪力和弯矩的峰值详见表2-3.为了更清楚地进行对比，采用的是两两对比.

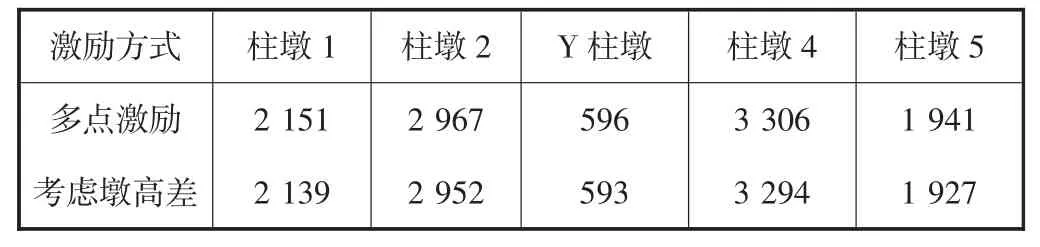
表2 各个桥墩墩底剪力峰值比较 kN

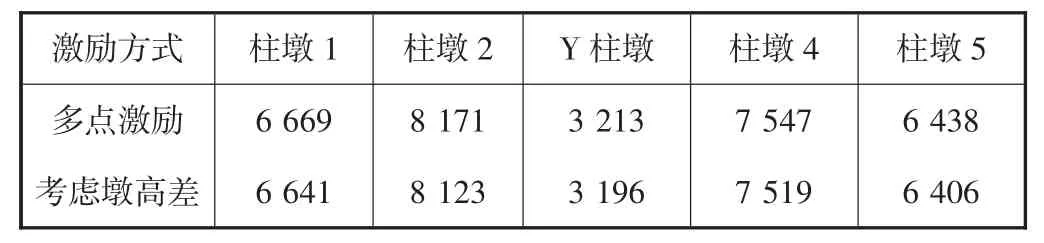
表3 各个桥墩墩底弯矩峰值比较 kN·m

从表2-3可知，在考虑墩高差影响的多点激励下各桥墩墩底剪力和弯矩均小于在多点激励下各桥墩墩底的剪力和弯矩，但相比之下相差很小.

模型二在多点激励，考虑墩高差的多点激励下，各个桥墩墩底剪力和弯矩的峰值详见表4-5.

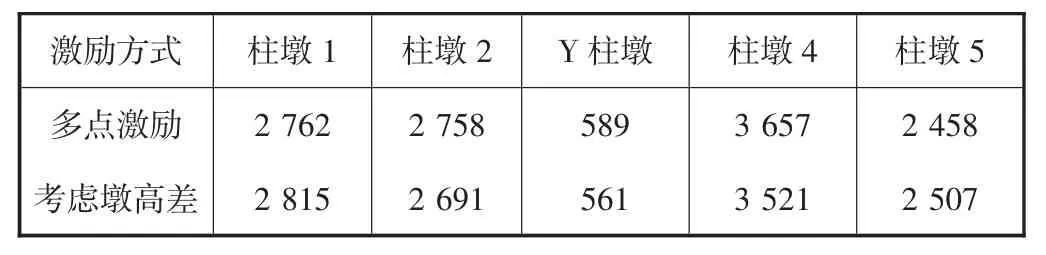
表4 各个桥墩墩底剪力峰值比较 kN

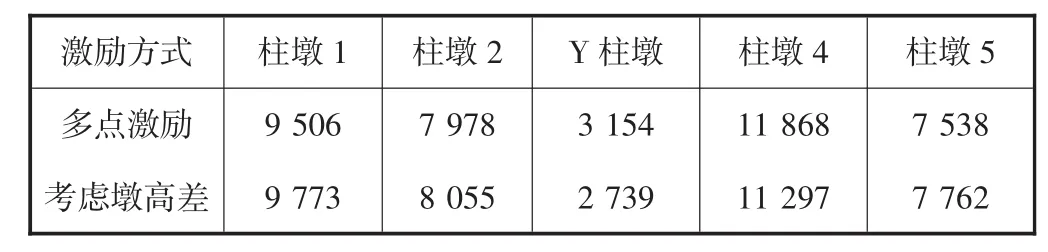
表5 各个桥墩墩底弯矩峰值比较 kN·m

从表4-5可以看出，多点激励和考虑了墩高差的多点激励相比，各桥墩墩底剪力和弯矩变化较为显著，并且在这两种不同激励方式下，不同桥墩墩底剪力和弯矩大小变化不一，各有增减.

从表2、4以及表3、5可以看出，两个模型在同一种激励方式下，相同的桥墩墩底剪力和弯矩变化显著，并且大小变化不一，各有增减，相同位置内力相差最大可达50%.

5 结论

（1）模型一和模型二在同一种激励方式下，相同点地震内力相差很大，因高墩数量的增加，使得桥梁的整体柔性变大，同时改变了桥梁的频率，使桥梁在同一种激励方式下地震响应相差很大.

（2）对于大跨高低墩连续拱桥，当高墩数量较少时，在考虑墩高差影响的多点激励下各桥墩墩底剪力和弯矩均小于在多点激励下各桥墩墩底的剪力和弯矩，但相差很小.随着高墩数量的增加，在考虑了墩高差影响的多点激励下，各桥墩墩底剪力和弯矩与多点激励相比变化较为显著.但是在这两种不同激励下，不同桥墩墩底剪力和弯矩大小变化不一，各有增减.

（3）对于大跨高低墩连续拱桥，在进行桥梁结构抗震设计计算时，不同工况下桥梁的地震响应有所不同且最危险的状态并不一定出现在某一特定工况下.因此，建议各工况取包络的方式选取最不利状态作为结构的设计依据.