超载下高支模碗扣式架体单元组装方式分析

丁克胜，赵永强，李耀祖

（天津城建大学 土木工程学院，天津 300384）

在现代建筑结构施工中，模板及支撑架体支设是主要的施工过程，其中的支撑架体多数采用满堂红式.模板及其支撑架体在钢筋混凝土结构主体工程施工中，其劳动量占1/2左右，尤其近些年随着高层和超高层及大空间建筑结构的发展，所需的超高超载的大面积支撑架体越来越多，其劳动量所占的比例更大，支撑架体的搭设时间更长，同时在大面积的满堂红支撑架体中还存在许多不必要的搭设空间[2].为了解决现场拼装劳动量过大的问题，更大限度地节约搭设时间和材料，研究一套适宜结构设计模数、可组装的标准化超高超载支撑架体尤为重要.所谓超高是指架体支设高度超过8 m，超载是指承受施工总荷载在15 kN/m2及以上，施工线荷载在20 kN/m2的支撑架体（住房和城乡建设部的建质[2009]87号文件的规定）[3].同时对超高超载的大型荷载作用下支撑架体的稳定性提出了更高的要求.

本文旨在通过SAP2000有限单元法程序，对碗扣式超高超载支撑架体进行分析，从空间上探索碗扣式支撑架体立杆荷载的分配规律与传递规律，为其标准单元的合理优化布置提供数据和理论依据，从而找出碗扣式钢管整体支撑架的简洁、节约时间和材料的优化方案[4].

1 有限元模型的建立

根据《建筑施工碗扣式钢管脚手架安全技术规范》（JGJ166—2016）的相关规定和构造要求，结合现在工程实际，首先建立三步三跨（水平杆步距1.2 m，立杆纵横向间距均为0.9 m）的单元架体，其模型如图1所示，将其组装成不同空间的支撑架体形式.本文以某工程搭设尺寸为背景，建立的模型尺寸为：X、Y方向21跨×0.9 m=18.9 m，Z方向18步×1.2 m=21.6 m，具体模型如图2所示.

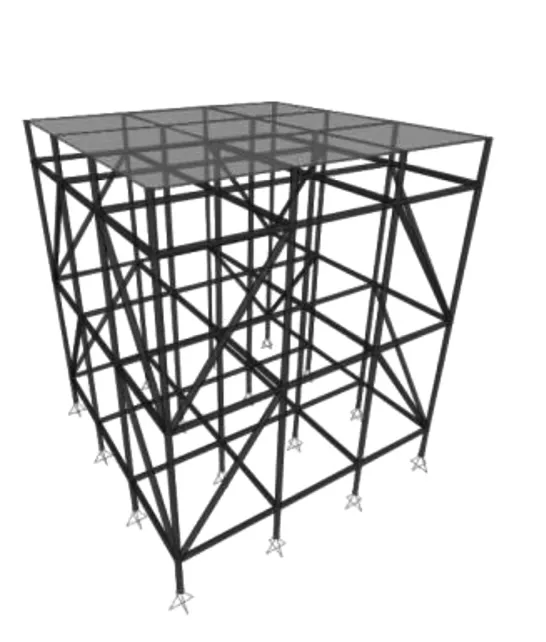
图1 单元架体模型

图2 组装模型

2 数值模拟计算结果分析

为了分析支撑架体的内力分布规律和影响其整体稳定的因素，结合目前施工现场实际，建立如图3所示的三种单元架体的平面布置方案（图中画阴影为单元架体），即：将原三步三跨模型架体单元依次按照“满堂红型”、“矩阵型”、“梅花型”布置.其中，单元架体之间每个节点通过水平杆件相连，顶层、扫地杆、外围布置斜杆，组装成相应空间结构体系[5].架体的承载力计算依然按照稳定性验算来计算，根据公式N/ΨA≤f，由立杆轴力控制，因此，分别对三种模型分别施加15 kN/m2均布荷载，比较三种不同布置形式下的立杆的最大轴力及轴力分配规律[6].

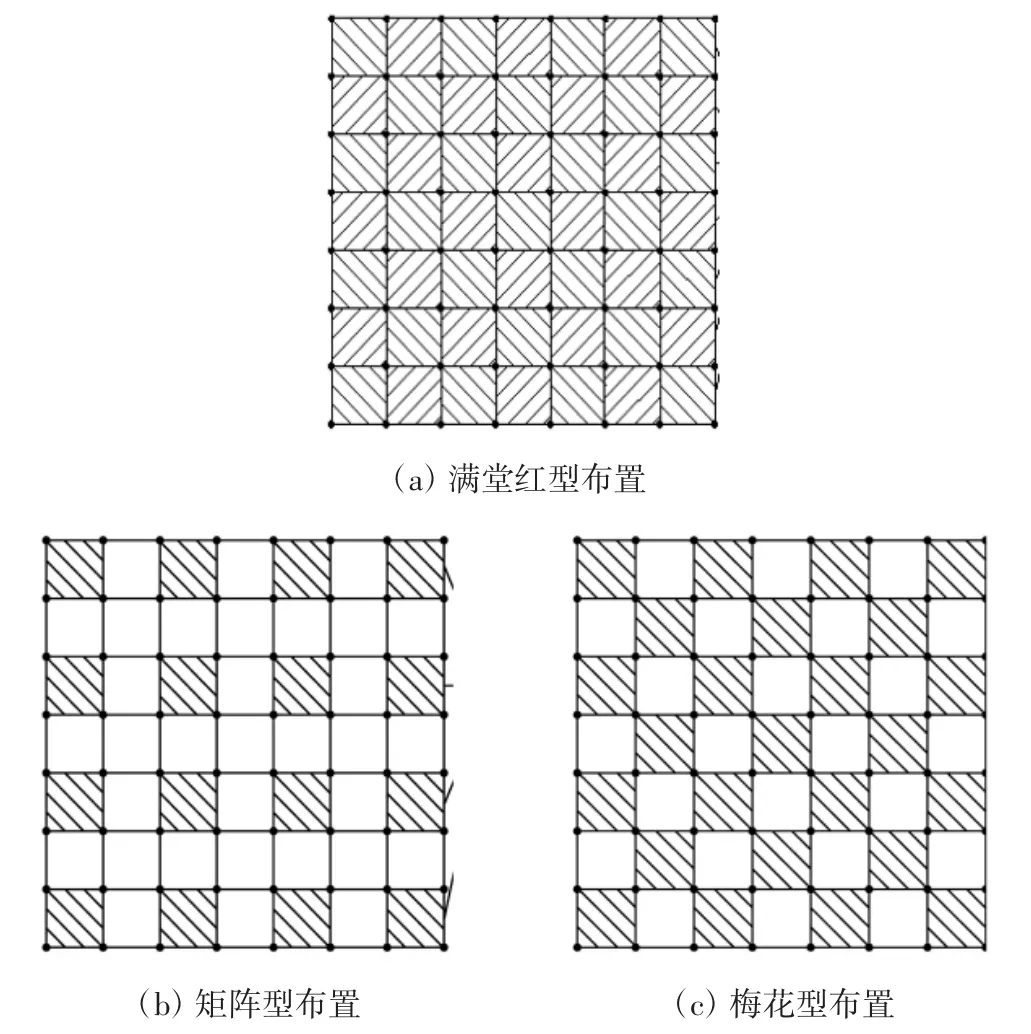
图3 三种不同布置方式示意

2.1 满堂红型布置支撑架体立杆内力分析

在15 kN/m2的竖向荷载作用下，采用满堂红立杆布置，选取不同横行架体，对立杆在不同位置，不同高度的轴力进行分析[7].

（1）Y=0时的横行立杆轴力分析（架体边缘）.Y=0立面的一横行排架立杆位于模型的最边缘，其在不同高度、不同水平位置的轴力曲线如图4所示.

由图4a可以看出，在同一标高Z=0.85 m处截面，X=0，2.7，5.4，8.1 m轴线上的立杆轴力偏大.这是因为这些位置与竖向斜撑相连，立杆上的轴力部分来自斜撑导致轴力增大突变，说明竖向斜撑可以协调立杆传递竖向荷载.而在其他标高截面，X=0，2.7，5.4，8.1 m轴线处立杆轴力较之相邻高程处突然减小，也是因为竖向斜撑将与之相连的立杆轴力传递分配出去，并且分配比例大致相同.因此，竖向斜撑可以协调整个架体的内力重分布[8]，增加了架体受力的整体性.

由图4b可以看出：在X方向（横行），立杆的轴力自边缘向中部有缓慢减小趋势；在X=0.9 m轴线处立杆轴力明显增大.这是因为近边端立杆并不像中间部分的立杆那样可以很好地把内力传递分配出去，而且也不像X=0 m处的立杆有竖向斜杆的支持，所以出现立杆轴力比较大的不利状况.

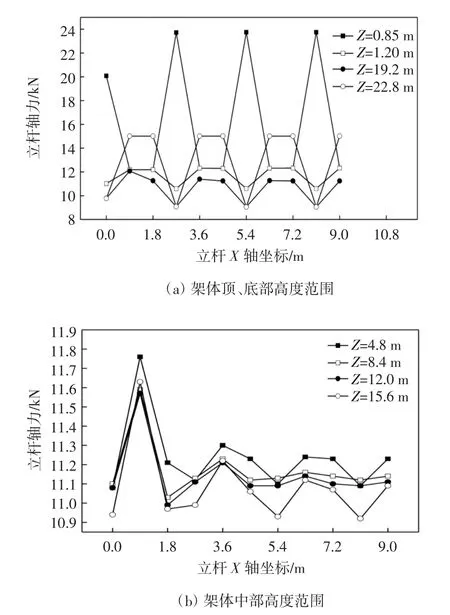
图4 Y=0横行立杆不同高度的轴力曲线

从图4可以看出，对于同一根立杆，除顶层外，大体上是上部轴力小，下部轴力大，符合立柱受力特征.

（2）Y=4.5 m立面立杆轴力分析（架体的1/4位置）.Y=4.5 m的横行立杆位于所建模型的1/4边长位置，其在不同高度、不同水平位置的数值模拟计算的轴力结果如图5所示.

从图5可以看出，该横行立杆上的轴力与Y=0横行立杆轴力的变化趋势极其相似，只是该横行立杆的底部截面的轴力相对增大，而其它截面的轴力相对减少.

图5 Y=4.5 m横行立杆不同高度的轴力曲线

（3）Y=8.1 m横行立杆轴力分析（架体中间位置）.Y=8.1 m横行立杆位于所建模型的中部，其在不同高度、不同水平位置的数值模拟计算的轴力结果如图6所示.

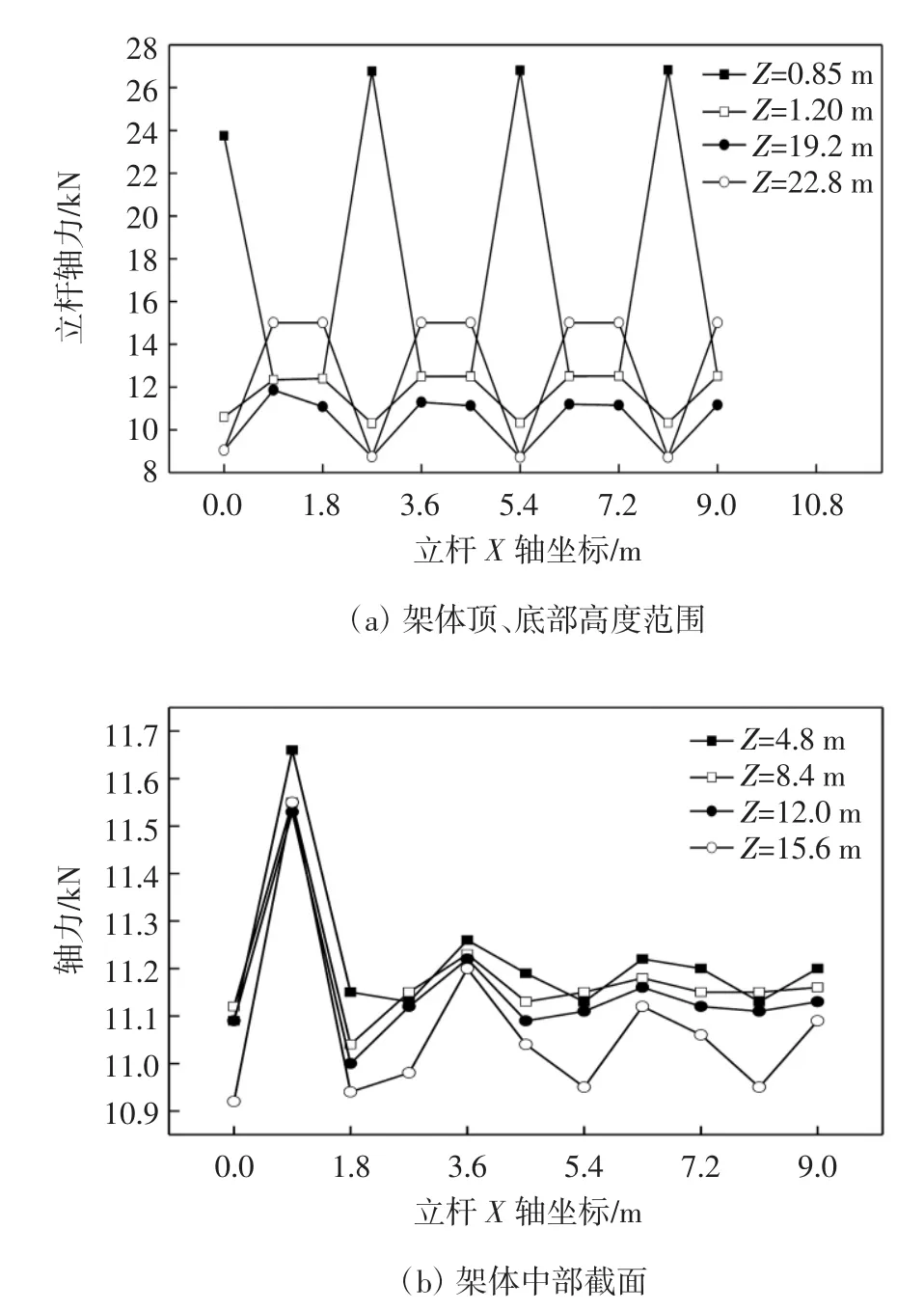
图6 Y=8.1 m横行立杆不同高度的轴力曲线

从图6可以看出，该横行立杆轴力与Y=4.5 m横行上的立杆轴力的变化趋势一致，在立杆最底部截面的轴力相对增大，而其它标高位置的轴力相对减小.

综合对以上三个沿Y轴截面立杆轴力变化趋势分析，同一根立杆而言，除顶层外，立杆轴力自顶端至底部逐渐增大；同一标高截面横向比较，支座截面有斜撑相连的立杆比没有斜撑相连的立杆轴力偏大，非支座截面处的变化趋势与之相反；立杆最大轴力出现于Y=8.1 m横行排架的X=0.9 m、Z=1.2 m的位置，其值为10.5 kN；总体上立杆的轴力自边缘至中部呈缓慢增大的趋势，这是因为中部立杆承受四个方向水平杆传递过来的荷载，即负荷面积大.

2.2 矩阵型布置支撑架体立杆内力分析

本方案选取与前面满布型相同的横行立杆位置和相同的截面进行相同的内容分析.

（1）Y=0时的横行立杆轴力分析如图7所示.

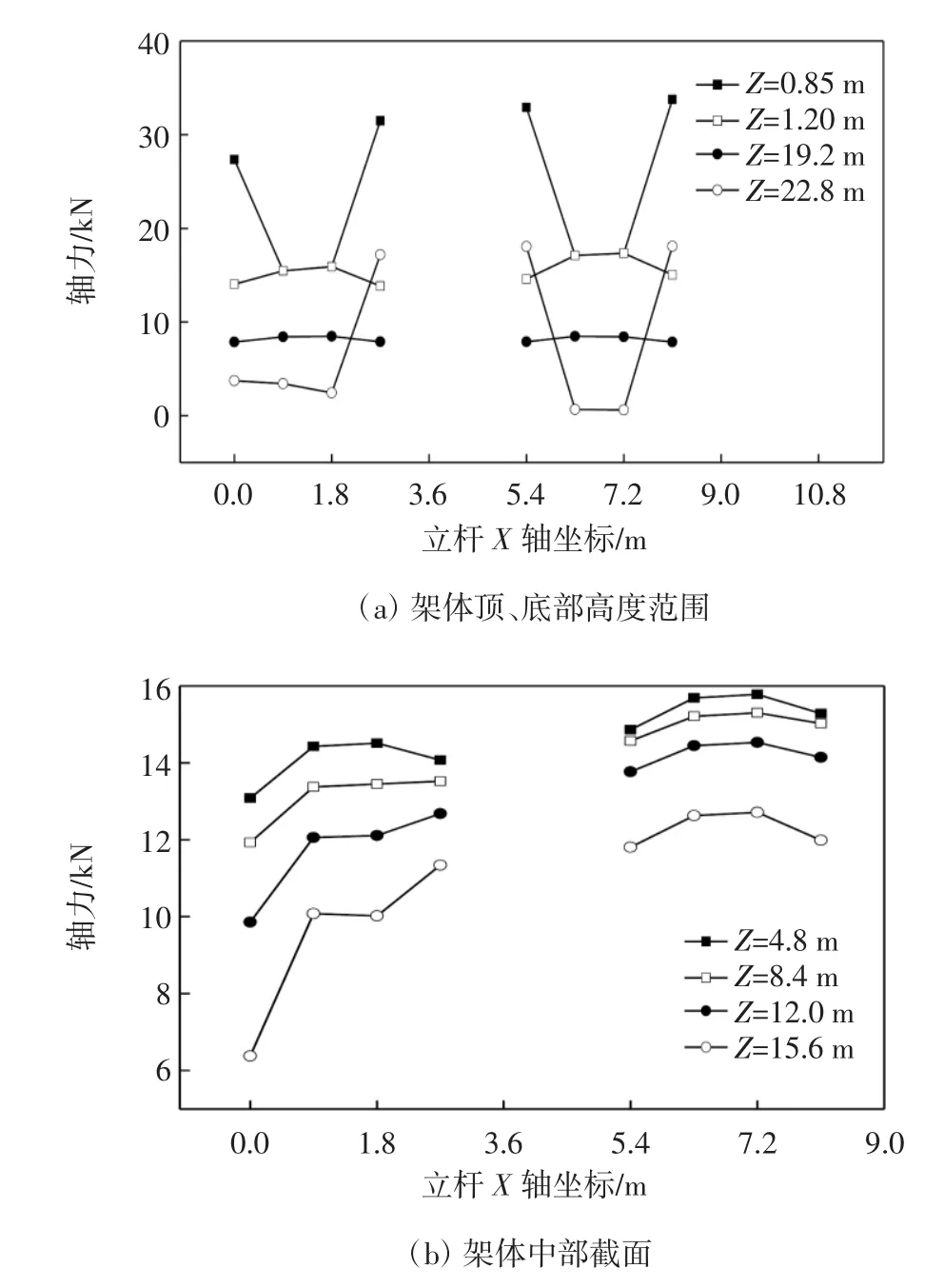
图7 Y=0横行立杆不同高度的轴力曲线

（2）Y=4.5 m立面立杆轴力分析如图8所示.

（3）Y=8.1 m横行立杆轴力分析如图9所示.

从图7-9可以看出：架体单元矩阵型布置时，有斜杆作用的立杆位置内力有突变；单元架体间不传递荷载，两单元架体之间的水平杆只起到连接作用；除支撑架体的最顶部外，立杆最大轴力出现在Y=4.5 m横行的Z=19.2 m、X=2.7 m位置，其值为23.5 kN（即：中部单元架体边角受力较大），比单元架体满布型轴力最大值增大了13.0 kN（不在同一位置）.从节约材料角度考虑，矩阵型布置比满堂红型布置节省杆件材料至少为67.35%.

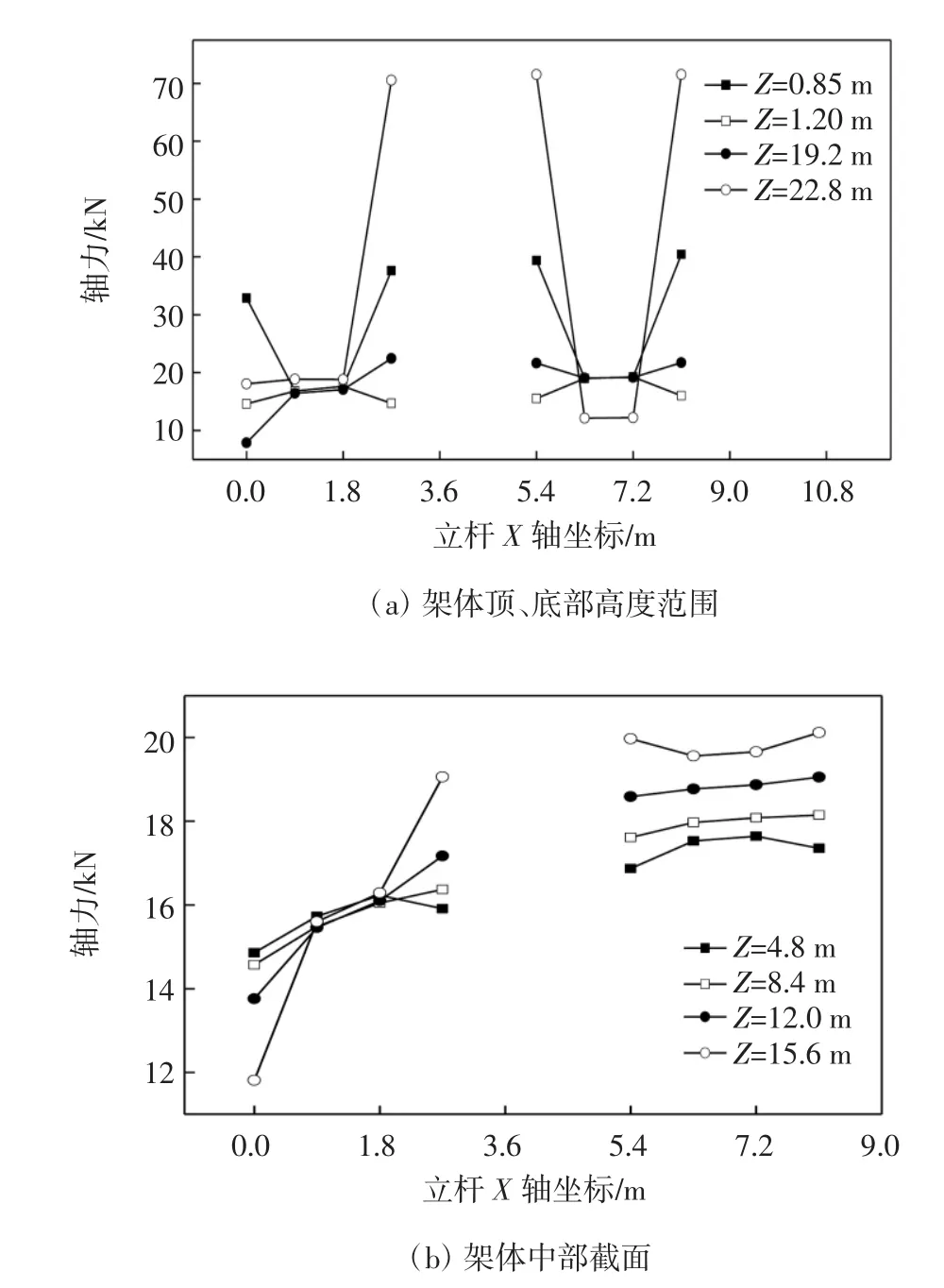
图8 Y=4.5 m横行立杆不同高度的轴力曲线

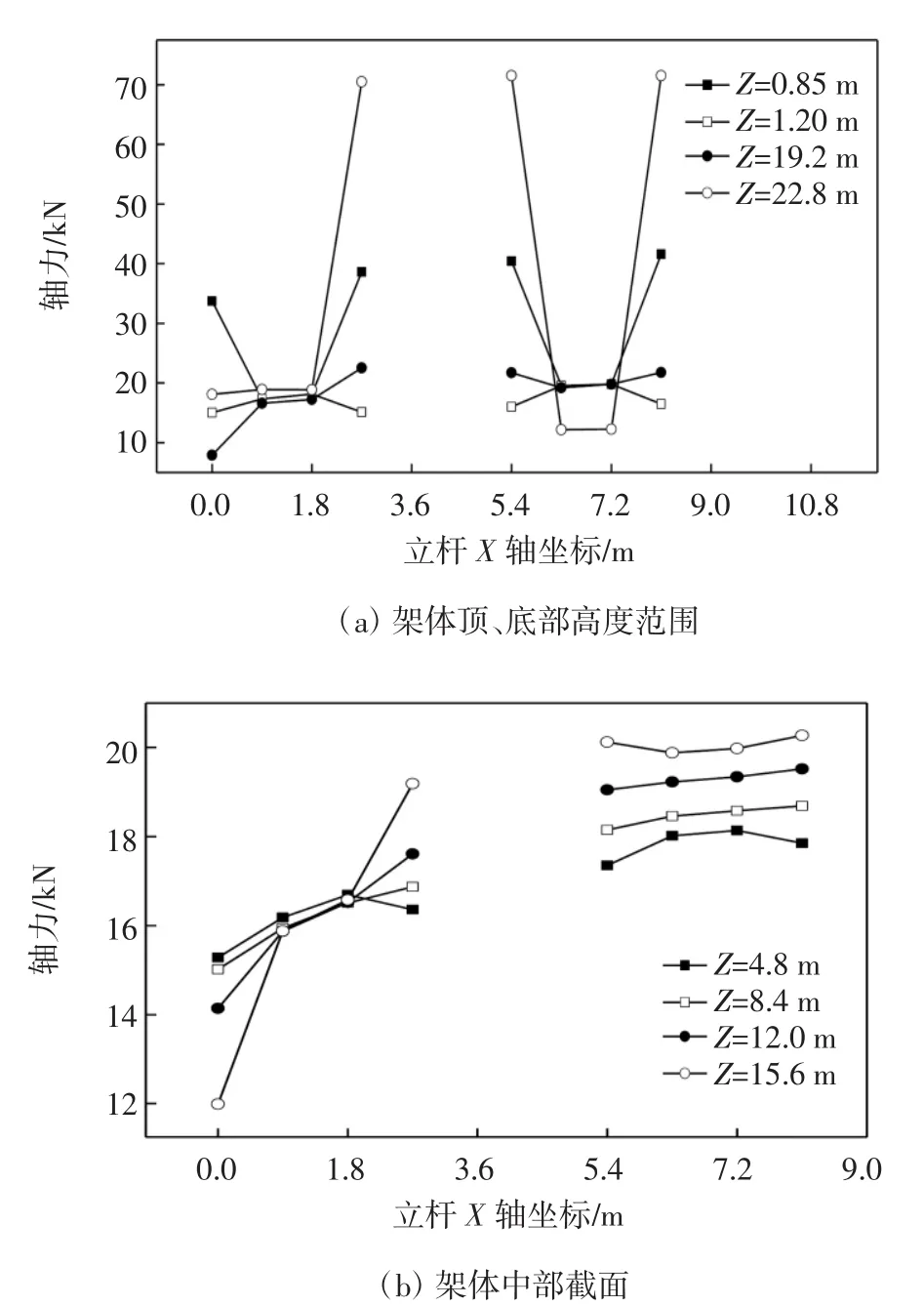
图9 Y=8.1 m横行立杆不同高度的轴力曲线

2.3 梅花型布置支撑架体立杆内力分析

选取与前面相同的方案，进行矩阵布置型的受力分析.

（1）Y=0时的横行立杆轴力分析见图10.

（2）Y=4.5 m立面立杆轴力分析见图11.

（3）Y=8.1 m横行立杆轴力分析见图12.

从图10～12可以看出：最外侧一横行的立杆轴力在顶部、底部是间断的，两单元架体之间所用水平杆只起连接作用；中部立杆两个方向有单元架体，所以均承受荷载；都有是除了顶部截面之外，立杆最大轴力出现在Z=19.2 m处，坐标为X=0.9 m，Y=8.1 m立面，最大轴力值为14.12 kN（即：中部单元架体的边角立杆），较之架体单元满布时轴力最大值增幅为34.35%；从节约材料角度考虑，梅花型布置比满布型布置节省杆件材料至少为48.98%；其它与满布型布置相似.

综上所述，承载力按从高到底排序，各种布置形式依次为满堂红型布置、梅花型布置、矩阵型布置；按材料用量从高到低排序依次为满堂红型布置、梅花型布置和矩阵型布置.虽然矩阵型布置材料用量最省，但是会出现较大内力，且边角较多，应力集中严重.综合分析，梅花型布置形式最值得采用.

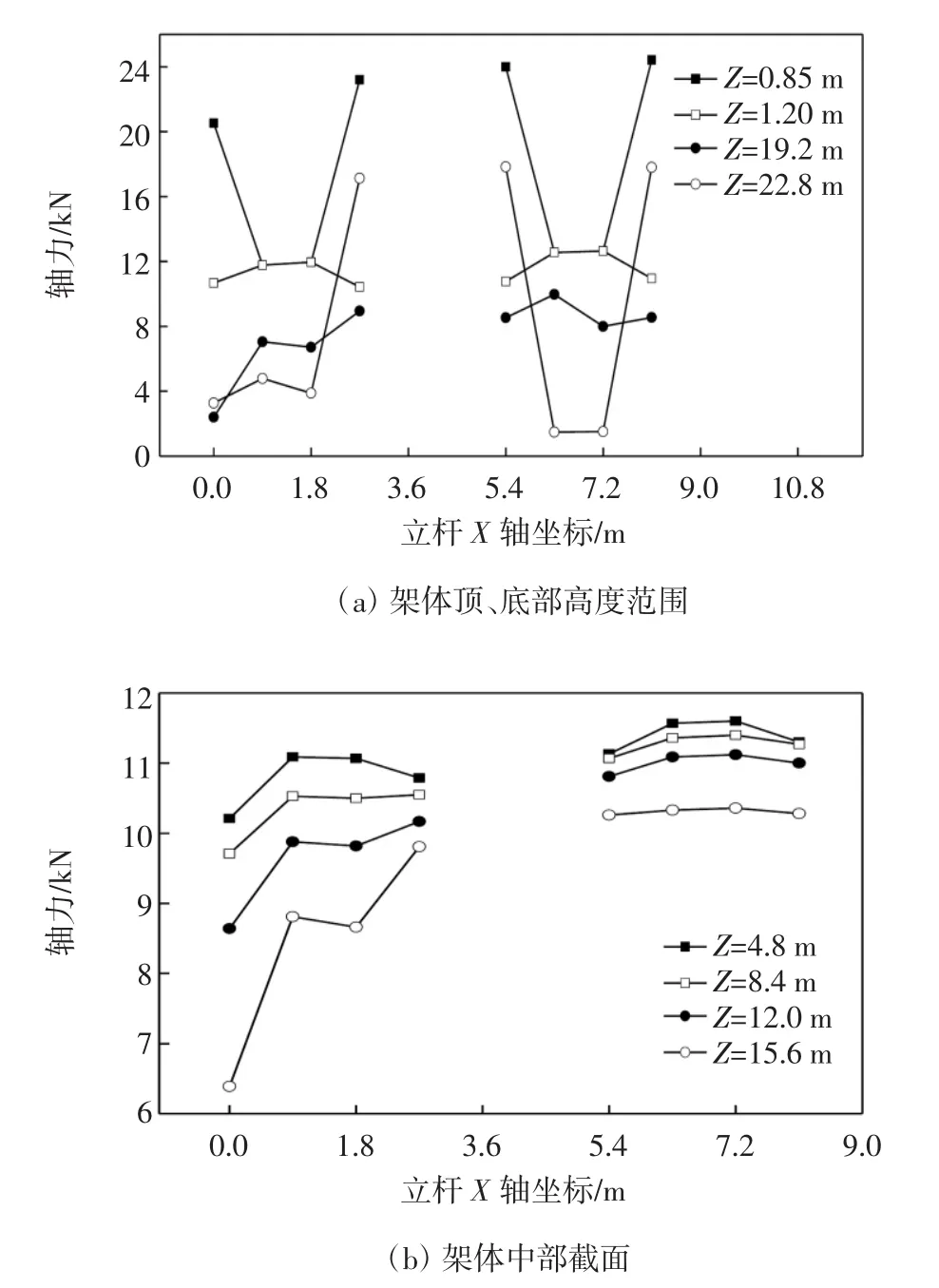
图10 Y=0横行立杆不同高度的轴力曲线

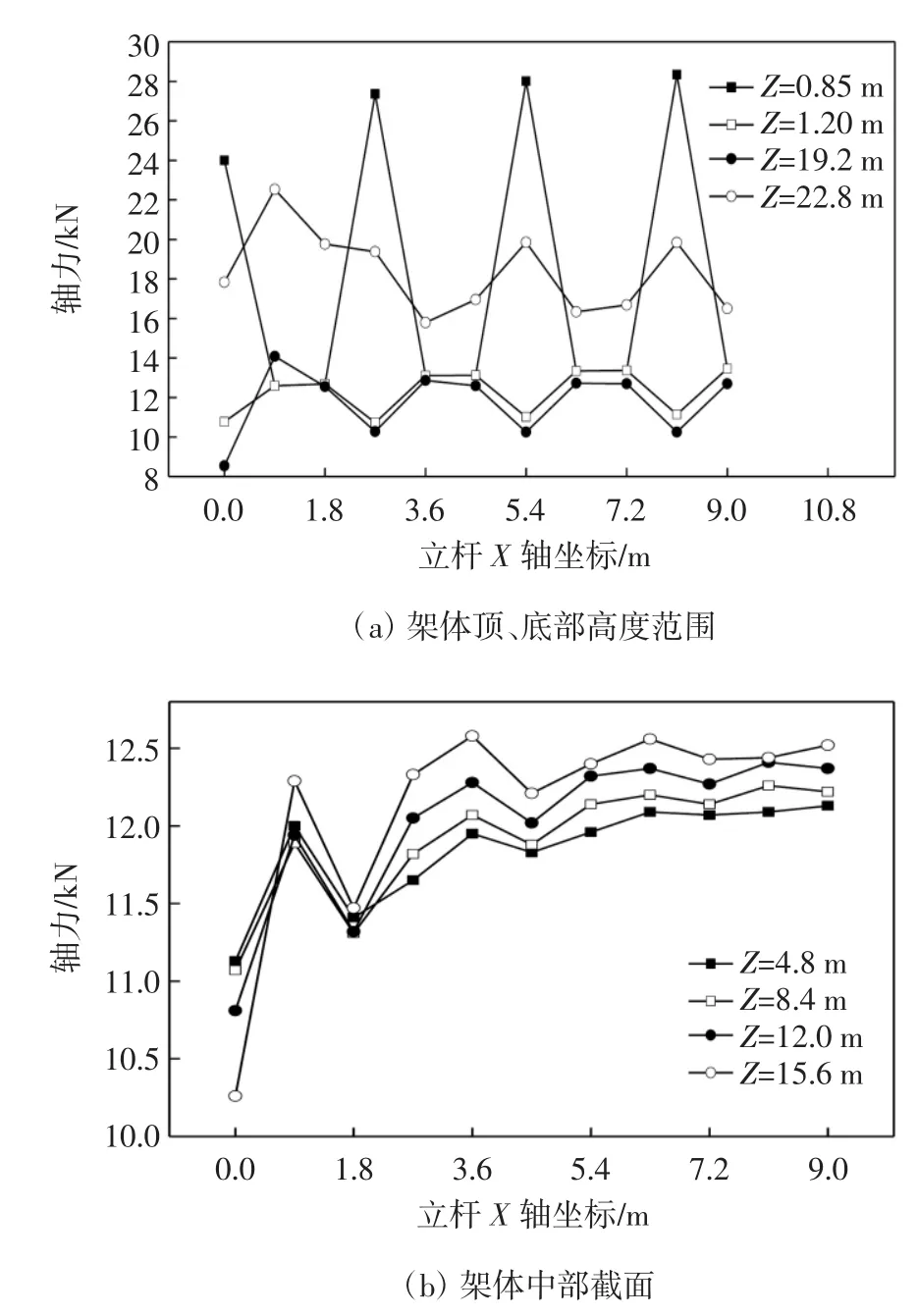
图11 Y=4.5 m横行立杆不同高度的轴力曲线

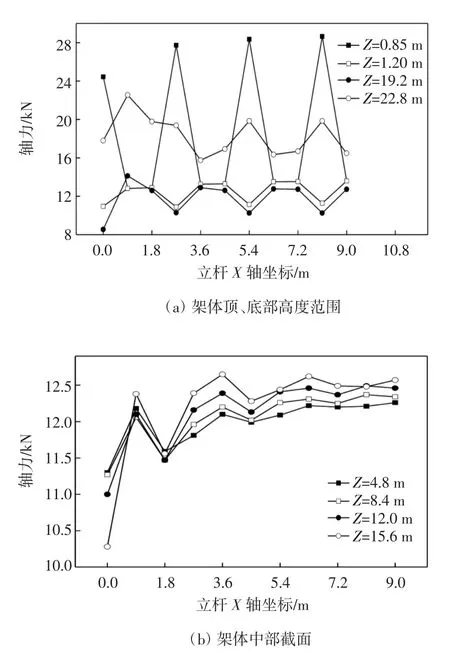
图12 Y=8.1 m横行立杆不同高度的轴力曲线

3 结论

通过对上述不同布置方案的超载超高支撑架体的数值模拟分析，得出如下结论.

（1）对于同一根立杆，除顶层外，轴力自上而下逐渐增大；同一标高截面，立杆的轴力自边缘向中部有缓慢增加的趋势.

（2）架体内力的横向传递能力较弱，对水平杆可以得出的主要作用是为立杆提供支撑.

（3）架体中的水平斜杆主要作用是对所在层架体提供水平约束，对稳定承载力几乎无贡献；竖向斜杆可以协调立杆的传力路径，传递竖向荷载，从而改变了架体的失稳模态.

（4）当单元架体采用不同方式布置时，从架体受力角度、材料用量角度综合衡量，梅花型布置效果最好，可以优先考虑.

本文的上述研究结论可为今后采用碗扣式支撑架体的不同支设面积的大空间结构工程施工在减小劳动强度、缩短搭设时间、减少材料用量、降低工程成本方面提供可靠的理论保障.