地基冻胀条件下碗扣式模板支架稳定承载力分析*
徐 嫚 李晓明 刘昌永 魏晨阳 王庆贺
(1.东北林业大学土木工程学院, 哈尔滨 150040; 2.哈尔滨工业大学结构工程灾变与控制教育部重点实验室,哈尔滨 150090; 3.沈阳建筑大学土木工程学院, 沈阳 110168)
0 引 言
碗扣式支架作为模板支撑体系中常用的结构形式,在工程施工中用于承受各类施工荷载,由于其整体受力性好、安全性高,且支架纵横向间距、步距均为制式化,因此在工程施工领域应用广泛[1]。碗扣式模板支架结构杆件众多且受力复杂,由于施工设计不规范、管理不严谨以及地基处理不当等因素,导致碗扣式模板支架事故屡禁不止[2]。
对于我国东北等高寒地区,冬季时节温度低且时间长,环境温度的变化对工程施工影响较大,实际施工的有效工期短,不少工程施工存在抢工期现象,在秋冬交替与春冬交替时节进行施工[3]。碗扣式支架作为工程施工的临时结构,支架地基处理的重要性往往被忽视,当温度下降幅度较大时,土体中由于自由水过多出现冻胀现象,导致碗扣式支架出现地基隆起,造成部分支架立杆向上提升。当碗扣式支架处于搭设阶段时,地基隆起所造成的立杆提升可通过调节天杆高度等措施保证碗扣式支架施工安全性,如图1所示;当碗扣式支架处于上部持载阶段时,地基隆起所造成的立杆提升会导致支架整体受力发生变化,严重危害工程施工的安全性。
目前,国内学者针对碗扣式支架受力性能进行了大量研究。周康喆通过试验与有限元计算,对碗扣式支架的受力性能进行研究[4],提出了立杆计算长度的修正计算公式。冉涛等通过MIDAS研究支架高宽比对支架承载力的影响,发现碗扣式模板支架的承载力随着支架高宽比的增大而显著降低[5]。方诗圣等认为支架杆件初始缺陷可等效为节点处0.015Pu假想水平力,并基于此对支架承载力的影响因素进行研究,发现当地基符合JGJ 166—2016《建筑施工碗扣式钢管脚手架安全技术规范》[6]设置时,立杆底部脱落对支架承载力的影响可忽略不计[7]。张晓静通过现场监测与有限元计算,研究了施工期间支架的受力性能,认为“回字形”浇筑可确保支架整体受力的均匀性[8]。孙秋月基于试验与有限元计算,研究立杆步距与斜撑设置对支架承载力的影响,发现步距减小与增设斜撑均能有效提高支架承载力,在相同条件下,增设斜撑对支架承载力的提高更为显著[9]。邹阿鸣等基于ANSYS有限元软件分析验证了三折线模型模拟碗扣节点的准确性,并进一步研究立杆脱空对支架的影响[10]。
综上,各学者针对碗扣式支架的受力性能进行了系列研究并得出许多有益的结论,但是针对实际工程中地基处理不当引起碗扣式支架受力性能变化方面的研究较少。因此本文以某实际桥梁工程碗扣式支架搭设为依据,基于ABAQUS有限元软件建立三折线半刚性碗扣式支架模型,考虑碗扣式支架的材料非线性与搭设缺陷,对因土体冻胀导致支架地基隆起后的碗扣式支架受力性能进行分析。
1 考虑地基隆起的碗扣式模板支架有限元建模
结合文献[8]中4组碗扣式支架试验结果,采用ABAQUS对碗扣式支架进行受力性能分析,验证建模方法的可靠性,为研究碗扣式模板支架体系的受力性能提供依据。
1.1 碗扣式模板支架节点的三线性模型
碗扣式模板支架体系中,立杆与水平杆作为主要受力构件,承受支架上部荷载;碗扣节点作为连接支架立杆与水平杆的重要构件,起传递立杆间的弯矩与水平杆剪力的作用。
针对碗扣式支架进行受力分析时,一般将碗扣式支架简化为刚接、铰接与半刚接体系[11]。我国JGJ 166—2016[6]提出,模板支撑架结构的碗扣节点应为半刚性,且节点转动刚度为40 kN·m/rad。但是,碗扣节点在实际工程搭设时,不可避免地存在部分初始缺陷,研究人员通过节点试验发现,碗扣节点由于初始缺陷的存在,导致碗扣节点前期转动刚度较小,随着荷载持续增加,碗扣节点间受力逐渐克服初始缺陷,节点间隙变小,碗扣节点转动刚度迅速增大,到达一定数值后增幅减缓,直至节点转动刚度趋于极限数值[12-15]。文献[12]认为,采用三线性模型可准确反映碗扣节点的实际转动刚度,其中三折线半刚性节点连接模型如图2所示,碗扣节点转动刚度具体参数见表1。

表1 三折线模型参数[12]
1.2 碗扣式模板支架有限元模型验证
1.2.1试验模型
文献[8]中设计4组支架足尺试件,通过固定支架纵横向间距、扫地杆高度以及天杆高度,分析步距与斜撑的改变对碗扣式钢管满堂支架受力性能的影响,具体试件参数详见表2,典型试件构造见图3。试验所用杆件均为国标杆件,采用Q235级钢管,外径48.3 mm,钢管壁厚3.5 mm。

表2 试件参数[8]

a—平面; b—立面。
试验采用力-位移控制加载方式,试验加载共分5步,1~4步为力控制加载,按试验荷载的25%设为荷载量逐步施加,每步加载后持荷5~10 min,统计测点数据,观察支架整体变形状态;第5步采用位移控制加载直至支架失稳破坏。通过全站仪观测支架各杆件变形。具体加载与量测方案见文献[8]。
试验中4组足尺试件破坏时立杆均为半波弯曲,其中SJ-1与SJ-2支架为整体弯曲失稳,SJ-3与SJ-4支架为局部失稳,各试件承载力见表3。可以发现:SJ-2与SJ-1相比,剪刀撑的设置可有效提高支架整体承载力;立杆计算长度与步距成正比例关系,当立杆步距减小时,支架立杆刚度大幅提升,碗扣式支架承载力变大,因此SJ-3单杆承载力大于SJ-1;SJ-4在加载时出现意外,由于支架天杆的破坏导致架体发生严重失稳,支架承载力大幅度下降。

表3 试件承载力
1.2.2模型验证
由于SJ-4支架在试验中发生意外,因此选取SJ-1~SJ-3支架进行受力分析,验证建模方法的可靠性。支架各杆件均采用Q235级钢材,钢材弹性模量E取2.06×105MPa,屈服强度为235 MPa,钢材本构关系见图4。
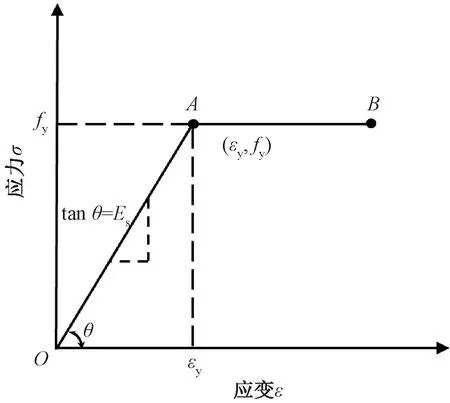
图4 材料本构性能
采用ABAQUS有限元软件按照支架实际搭设状况建立碗扣式支架三维有限元模型,支架水平杆、立杆与剪刀撑采用Wire单元模拟;支架立杆与水平杆相连的碗扣节点采用Hinge单元模拟,模拟图2所示的三折线半刚性节点连接性能;支架剪刀撑与立杆相连的扣件采用Hinge单元模拟,并设为铰接。支架底端设为铰接约束,支架顶端限制水平两方向位移,在支架天杆上端施加集中荷载。ABAQUS模型如图5所示。
a—SJ-1; b—SJ-2; c—SJ-3。
碗扣式模板支架在实际搭设中难免存在垂直度偏差,我国JGJ 166—2016中规定:架体全高的垂直度偏差应小于架体搭设高度的1/600,且不得大于35 mm。因此,本文采用考虑初始缺陷的EBM法[16]对碗扣式支架进行受力分析,即对支架模型进行线性屈曲分析,得到支架一阶屈曲模态,并设该模态最大位移取1/600的架体高度作为支架搭设缺陷,施加到支架模型中。各组试件的单杆平均承载力与试验结果对比见表4。
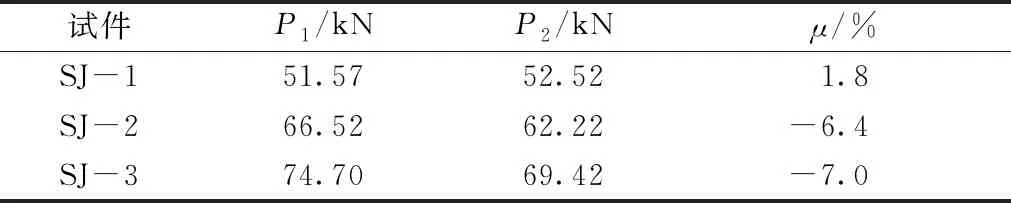
表4 单杆平均承载力有限元分析与试验结果对比
由表4可知,SJ-1~SJ-3支架模拟最大偏差为7%,模拟结果较为理想,表明所建立的有限元模型可以较为准确地模拟支架体系的实际受力状态。有限元分析时所采用的EBM法是基于支架搭设的最大偏差条件,且各立杆上端均匀承受轴心荷载,但是试验中按规范[6]搭设的碗扣式支架垂直度偏差较小,且荷载施加难以保证均通过立杆轴心,这些因素导致两者的计算承载力存在些许差异。
1.3 模型的选定
对于我国北方地区,在秋冬交替以及冬春交替时节,白天最高温度达10 ℃,夜间最低温度达-10 ℃,环境温度变化较大、温差显著,极易导致土体产生冻融现象。当支架地基中自由水含量大于土体冻胀含水量、环境温度的变化较大、温度降低至土体起始冻胀温度时,土体中的自由水就会发生冻结,体积膨胀达9%[17],导致支架地基隆起,如图6所示,造成部分支架立杆向上提升,严重危害支架整体受力性能。

图6 支架地基隆起现象
立杆下部地基隆起,引起支架立杆底端产生上部位移Δ1,由于支架水平杆的存在,限制立杆发生较大变形。如图7地基隆起受力简化所示,立杆因地基隆起发生位移Δ1可简化为立杆所受轴力Fly,与立杆相连的扫地杆可简化为立杆在碗扣节点处所受轴力Fh1、Fh2、Fh3、Fh4。由图7可知,支架地基隆起后,不仅会导致碗扣架体发生一定变形,还会改变架体的荷载传递路径。

a—地基隆起示意; b—地基隆起受力简化。
对于碗扣式支架结构,根据支架立杆与水平杆的受力特性,可通过简化力学模型的方法模拟立杆受力,水平杆与剪刀撑对立杆的约束可简化为弹性支座,因此支架立杆的力学模型可简化为有多个弹性支座的多节间连续压杆,如图8所示。由文献[18]可知,对于多支座弹簧刚度的连续压杆屈曲荷载Pcr的近似值可按式(1)计算:

a—碗扣式支架模型; b—立杆力学模型简化。
(1)
式中:E为立杆的弹性模量;I为立杆的截面惯性矩;H为立杆总高度;n为连续压杆屈曲时的半波数。可按式(2)计算:
(2)

式中:h为支座间距(即立杆步距);k为支座的弹簧刚度,文献[19]中指出,应从结构的特性与材料的安全性考虑弹簧刚度,并给出相应的计算公式;l为立杆间距;Qb为下碗扣抗剪强度设计值[6]。
当立杆的屈曲荷载与立杆破坏时的最大轴力P相等时,此时忽略构件的水平变形,仅考虑构件竖向位移,可得立杆高度与竖向位移关系式:
(3)
式中:Δ为荷载作用下支架立杆的总竖向位移,考虑实际工程中土体冻胀隆起时,立杆上部已承受部分恒载,因此支架立杆的允许隆起高度计算公式为:
(4)
式中:P1为立杆上部恒载;Δ1为立杆允许隆起位移值。由式(4)可知,当碗扣式支架立杆间距与步距恒定时,立杆允许隆起位移随架体高度的增加而增大。由于简化模型未考虑构件初始缺陷以及水平杆对立杆的悬索作用,并且考虑到碗扣式支架体系受力复杂,因此需选用有限元进行相应的分析验证。
考虑到支架地基隆起时,架体上部承担混凝土自重和模板机具等恒定荷载,且在荷载作用下架体会产生一定竖向位移,由于混凝土及模板刚度较大,导致地基隆起时支架天杆不会产生竖向位移,因此在有限元中分两个分析步进行模拟:
1)模拟支架在上部恒载作用下整体受力。将支架立杆底端设为铰接,立杆上部限制水平两方向位移,并在支架立杆上端施加恒定集中荷载。
2)模拟恒载作用下地基隆起对支架的影响。对架体上部施加铰接约束,将未隆起立杆底端设为铰接,隆起处立杆底端应限制其水平两方向位移,通过施加竖向位移模拟地基隆起现象。
2 碗扣式模板支架地基隆起分析
2.1 工程案例
选取实际工程搭设的碗扣式支架进行研究,参照文献[7]的算例,采用ABAQUS建立碗扣式支架三维有限元模型。按照架体高度不同分支架1与支架2,支架1模型架体高7 m,四周布设竖向剪刀撑,如图9a所示;支架2模型架体高9.4 m,四周布设竖向剪刀撑,并按规范要求在支架顶层与中间层布设水平剪刀撑,如图9b所示。碗扣式支架详细参数见表5。
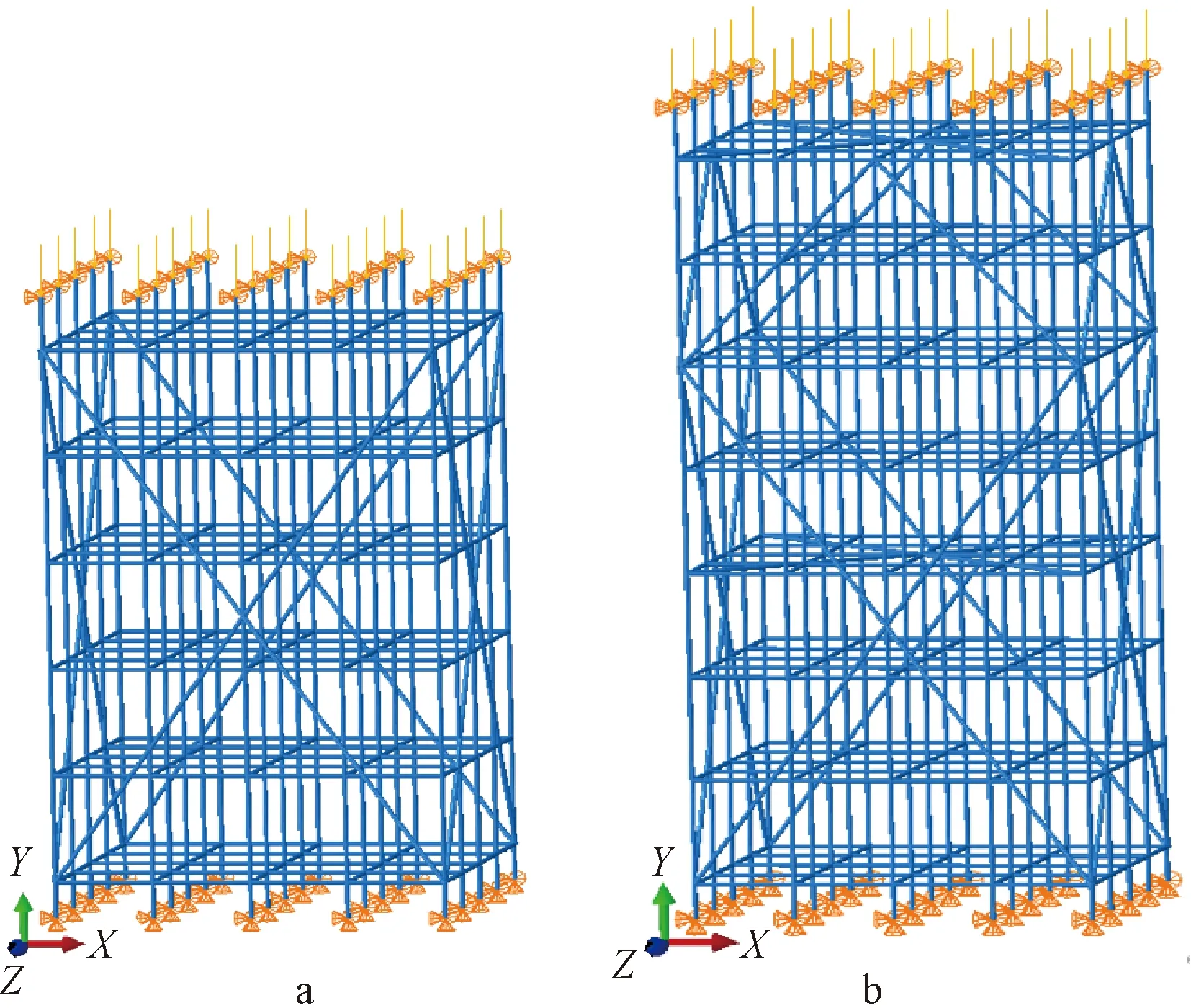
a—工况1支架; b—工况2支架。

表5 碗扣式支架详细参数
采用ABAQUS有限元软件对两种支架模型进行计算分析,研究支架的整体受力性能,计算结果见图10。可知:支架1稳定承载力为1 896.81 kN,支架2稳定承载力为1 363.45 kN,支架2较支架1稳定承载力下降28.12%,且支架1,2均为整体失稳破坏。

图10 碗扣式支架荷载-位移曲线
2.2 单根立杆基底地基隆起工况分析
恒载作用下碗扣式支架整体处于一种平衡状态,由于外界因素导致支架地基发生隆起现象,当地基隆起造成的轴力大于恒载作用下立杆所受轴力时,此时立杆处于一种假想平衡状态;随着土体冻胀程度加大,地基隆起造成的轴力将克服立杆自身刚度系数,并进一步导致立杆产生向上位移Δ1。对于忽略水平杆约束后的单根立杆,其抗隆起刚度通过计算可得,支架1为14.51 kN/mm,支架2为10.8 kN/mm。通过有限元软件分析支架地基隆起对支架受力性能的影响,设支架上部单根立杆恒载为30 kN,考虑到两种碗扣式支架模型为对称结构,因此选取立杆1~立杆9为研究对象,分析不同位置处的单根立杆基底地基隆起后对支架整体受力的影响,以及不同架体位置处的立杆允许隆起高度,支架立杆分布见图11。
通过有限元分析得到支架1、支架2的计算结果,见表6;选取典型位置处地基隆起进行水平杆受力分析,见表7;地基隆起处立杆荷载-位移曲线如图12所示。其中抗隆起刚度为立杆自身抵抗隆起变形的能力;允许隆起位移为地基隆起处立杆所受轴力最大时所对应的立杆隆起位移;荷载下降率是隆起后支架所受的极限荷载减去隆起前支架荷载之差与隆起前荷载的比值。
由表6、表7可知,支架允许隆起位移与架体高度成正比,与理论推导相符。对于支架1,2而言,支架失稳破坏时,水平杆最大应力均未达到屈服,支架主要由立杆破坏而引起支架失稳。其中,角部立杆隆起对支架影响较严重,此时支架抗隆起刚度最大达26.76,25.42 kN/mm,边部立杆抗隆起刚度次之,中部立杆抗隆起刚度最小。这是由于连接水平杆数目不同所引起,立杆向上隆起时,所受轴力Fly不仅由立杆自身承担,与立杆相连接的水平杆可简化为Fhx,与立杆共同受力。受水平杆连接数目的影响,中部立杆允许隆起位移最大,边部立杆次之,角部立杆最小。
以支架1为例,当支架上部恒定荷载施加完毕后进入持荷状态,此时支架立杆基底地基发生隆起,隆起处立杆水平位移随着隆起位移的增大而增大,如AB、AC段所示,当立杆隆起位移达到允许隆起高度时(即C点),此时隆起处立杆处于屈服状态,支架因局部杆件破坏而丧失稳定。由图12可知,立杆1(即角部立杆)基底地基隆起时立杆临界水平位移最小,立杆9(即中部立杆)基底地基隆起时临界水平位移最大,这是由于支架搭设缺陷的施加以及连接水平杆数目不同所造成。
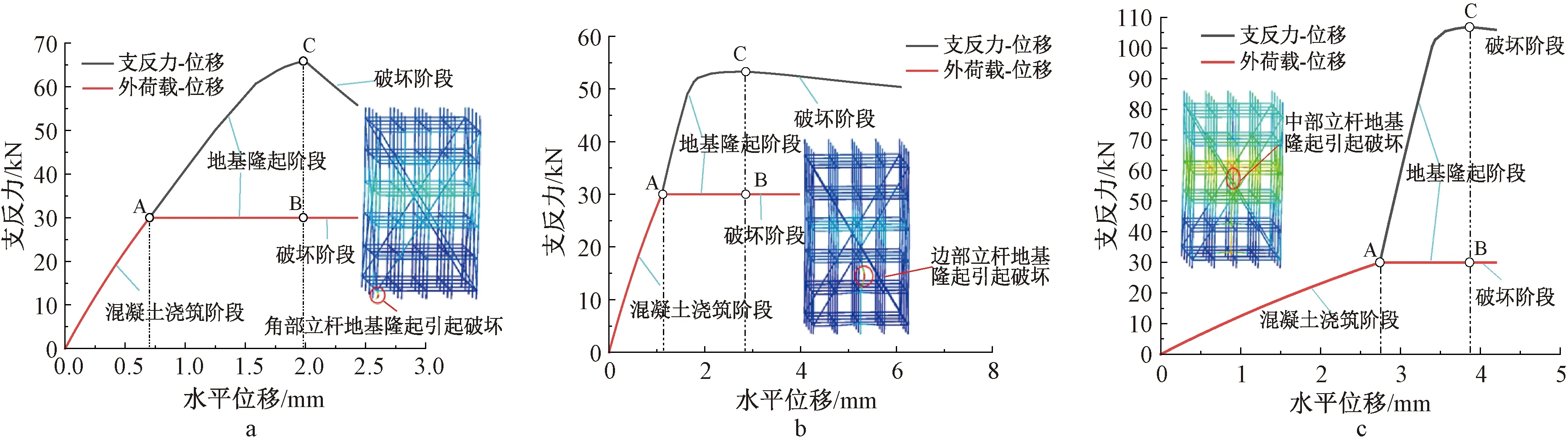
a—立杆1; b—立杆3; c—立杆9。
为分析两种支架模型在立杆基底地基隆起后的整体受力情况,选取碗扣式支架中的立杆1~立杆9,对立杆基底地基隆起以外其他杆件的轴力变化率(K)进行研究(K:正值为轴力减小,负值为轴力增大),见图13。可知,对于支架1与支架2,角部立杆与边部立杆隆起时各杆轴力变化较大,其中立杆1~立杆4和立杆7轴力变化相对显著,中部立杆隆起时各杆轴力变化相对较小。由于支架考虑搭设缺陷的影响,立杆隆起后为保持支架整体受力平衡,部分立杆的轴力出现不降反增现象。支架1与支架2整体受力差异与架体高宽比改变有关,支架2不仅在四周布设竖向剪刀撑,并按照规范要求布设水平剪刀撑,剪刀撑分别在竖向与水平向分担轴向力,立杆之间轴力传递路径复杂,导致各立杆所受轴力差异较大。

a—立杆1; b—立杆2; c—立杆3; d—立杆4; e—立杆5; f—立杆6; g—立杆7; h—立杆8; i—立杆9。
2.3 局部立杆基底地基隆起工况分析
考虑到实际工程中支架地基隆起为局部现象,因此选取4根立杆基底地基隆起情况研究支架整体受力性能。根据立杆与连接水平杆数目的不同,可分为角部立杆、边部立杆、中部立杆[9],因此分别选取角部、边部和中部立杆隆起进行分析,立杆隆起位置分别为角部(1、17、13、25);边部(4、7、19、21);中部(6、9、18、20),立杆位置示意见图11。
通过ABAQUS分析局部立杆基底地基隆起情况对碗扣式支架受力性能的影响,计算结果见表8。可知,对于支架1,2,支架失稳时水平杆仍未达到屈服状态,支架因立杆自身刚度不足而发生破坏;角部立杆隆起对支架受力性能影响最大,最大隆起高度为2.1 mm与2.3 mm,边部立杆隆起次之,中部立杆隆起影响最小。多根立杆基底地基隆起时,支架破坏模式属单杆失稳破坏,与单根立杆基底地基隆起破坏模式一致,因此支架失稳与立杆隆起根数无关,仅与立杆自身刚度有关。

表8 碗扣式支架局部立杆基底地基隆起分析
3 结 论
通过ABAQUS有限元软件研究实际工程中碗扣式支架的受力性能,重点分析支架地基隆起情况下对支架的影响,得到如下结论:
1)通过分析发现,在碗扣式支架立杆间距与步距一致情况下,支架因地基隆起而发生失稳破坏时,碗扣式支架的允许隆起位移随架体高度增加而增大。
2)支架地基隆起时,隆起处立杆受力最大,水平杆受力变化相对较小,其中角部与边部处立杆受力最为显著,支架1与支架2角部立杆抗隆起刚度分别为26.76 kN/mm和25.42 kN/mm,远大于单根立杆理论计算值。随着立杆隆起位移的增大,导致杆件屈服支架破坏,即支架极限荷载取决于隆起处立杆。
3)随着隆起根数的增多,支架各部位立杆允许隆起位移存在小幅度下降,但支架破坏模式仍属单杆失稳破坏,单根立杆隆起时承载力下降最大达58%,4根立杆隆起时承载力下降最大达51%。地基隆起情况下支架失稳与立杆隆起根数相关性较小,主要取决于立杆自身刚度。
4)支架地基隆起对支架受力性能的影响较为显著,其中角部和边部立杆受地基隆起影响最大。因此,在实际支架搭设工程中,确保支架地基坚实、均匀,并采取相应的排水措施进行处理,尤其是角部与边部处立杆地基,必要时应对支架地基采用换土垫层方法,有效杜绝地基隆起现象的发生。

