基于改进Dijkstra算法的移动机器人路径规划

王 旭，刘 毅，李国燕

（天津城建大学 计算机与信息工程学院，天津 300384）

移动机器人路径规划问题[1]是智能机器人研究领域中的核心之一，其本质是对图论研究中最短路径算法问题的引申.近年来国内外学者对于机器人路径规划问题进行过大量的研究，提出了多种移动机器人最短路径算法，如启发式搜索方法、神经网络方法、遗传算法[2]、蚁群算法[3-4]、人工蜂群算法[5]等.Dijkstra（迪杰斯特拉）算法[6-8]是一种典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径.它的主要特点是以起始点为中心向外层扩展，直到扩展到终点为止.该算法由于适应网络拓扑的变化，其性能稳定，因而在计算机网络拓扑路径选择、机器人路径规划以及GIS中应用广泛[9].Ammar等[10]提出松弛Dijkstra算法优化机器人路径规划，但是其结果可能存在较多不必要的路径转折消耗，甚至出现较大误差.且传统算法研究大多以0-1栅格化地图为基础，缺乏对于复杂地形环境下场景建模的兼容与支持.

近年来智能移动机器人发展迅速，作业环境日趋复杂，尤其以消防、救灾为目的的特种机器人对于有限空间及复杂环境下的作业能力要求越来越严格.现代智能机器人对复杂地形的适应度研究比较成熟，机械性能优良，越野避障能力水平较高.在复杂的地形环境下，传统二值栅格地图模型并不能满足机器人路径规划要求.

综合考虑移动机器人工作场景复杂程度以及算法的运行效率.本文提出构建一种蜂巢型地图模型对地理信息进行采样，并对机器人在地图中需要跨越的不同障碍物进行分析，贴近机器人实际工作场景，在提高算法计算效率的同时保证最优路径，保证消防救灾等特种机器人工作性能充分发挥.

1 经典Dijkstra算法

1.1 栅格地图建模

栅格法最早由W.E.Howden于1968年提出，其核心思想是将实际机器人工作环境抽象成为二值矩阵.算法中通常使用一个二维稀疏矩阵C[N][N]来存储整个交通网络中的数据，并以矩阵中的0-1描述机器人能否通过地图中某区域.栅格地图及其二值化处理结果如图1、图2所示.

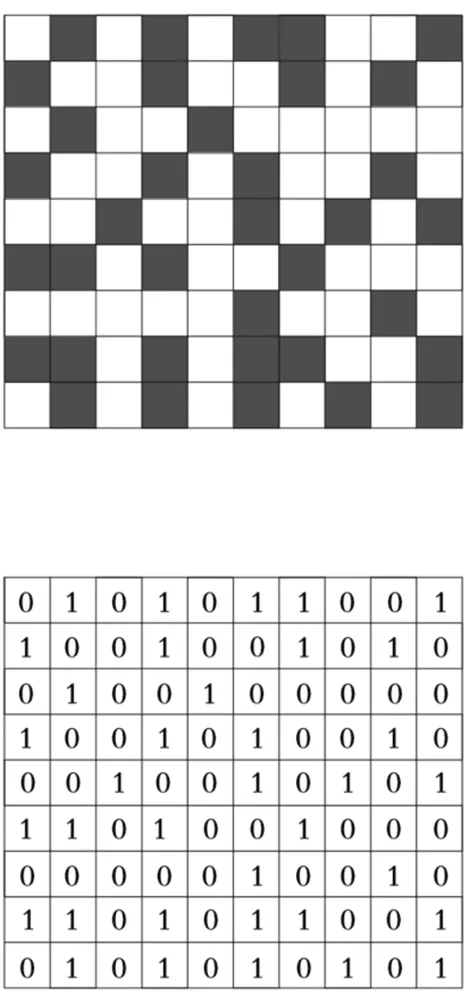
图1 栅格化地图模型示意

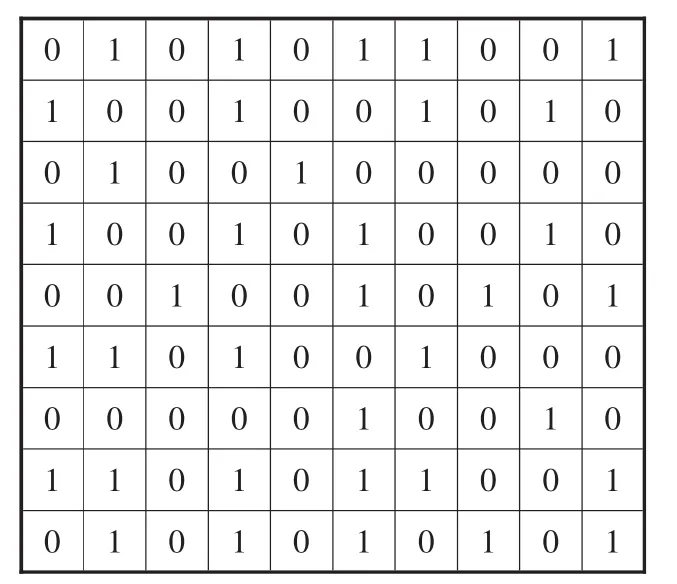
图2 二值地图模型示意

1.2 传统Dijkstra算法步骤

最短路问题是指在一个赋权图的两个指定点s0和t0之间找出一条具有最小权值的路径.

Dijkstra算法路径规划基本思路为：为每个节点j创建一组信息j（dj，pj，fj）；其中dj为地图中源点s0到当前节点j的最短路径长度（某节点与自身距离为0）；pj为源点s0到节点j的最短距离中到达节点j的前一节点；fj记录节点j的位置信息中dj值是否为空.

基本过程如下.

（1）初始化.源点s设置为：ds=0，ps为空，fs=true.除s外所有其它节点i（n）：di(n)=∞，pi(n)初始化为空，fi(n)=false，从源点处展开搜索.

（2）计算节点i（n）中所有fi(n)值为false点的di(n)值：di=min{di，dk+l}.其中：l为节点 j到节点 i的直线连接距离；k为源点到节点j的前一节点，即点j父节点.

（3）选取下一个节点：对于所有fi(n)值为false的点，将其di(n)值进行排序，选择di(n)值最小的点i作为当前节点，并设置pi=k，fi=true.

（4）当终点t满足ft=true时，算法结束，并沿pt逆序标出最短路径，否则转入（2）继续循环.

在栅格地图模型中，由于某一节点最多存在八个相邻子节点且距离不等，因此算法迭代过程中只能通过计算找出到距源点距离最小的节点作为当前节点才能继续扩展.由算法步骤可知，循环次数与节点数量成正比，计算时间将成倍增长.

在传统Dijkstra算法搜索过程中，每次迭代都需从Open表中找出距源点最近的节点作为当前节点进行扩展，并将其从Open移入Close表中.由于Open表中全部元素源点距离排序过程时间消耗较大，导致Dijkstra算法在路径规划研究中的计算效率较低.

2 改进Dijkstra算法

改进算法引入一种携带地形参数的蜂窝地图模型取代传统0-1栅格法地图模型，并简化迭代过程中的节点扩展机制，直接剪除传统Dijkstra算法在Open表中排序检索最近节点的过程，提高计算效率.

2.1 蜂窝地图建模

与传统栅格地图不同，蜂窝地图模型将原有地图划分为若干共临边正六边形网格区域，每个网格作为一个采样节点对地图中的相应位置地形数据进行采样.蜂窝模型初始化过程中，任意相邻节点间距离相等，即某节点最多存在六个等距相邻子节点，如图3所示.

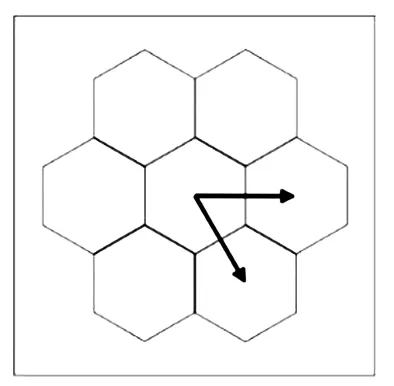
图3 蜂窝地图建模示意

在Dijkstra算法每次迭代过程中，由于各节点所有相邻节点距离均相等，因此改进算法直接跳过在Open表中对节点距离进行排序的计算过程.

2.2 地形影响

智能移动机器人在室外环境下作业时，地形条件很难达到理想通行情况.且对于大多数户外及特种机器人来说，路径规划算法难以考虑其部分涉水、攀爬及越障能力，造成机器人性能上的浪费.

复杂环境下移动机器人作业地形如图4所示.暖色区域（如红色、橙色）表示在地图中为凸起的山坡丘陵等地形，冷色区域（如蓝色）表示地图中的凹陷地形区域.移动机器人在较为复杂的沟壑、丘陵、泥泞等地形条件下的安全行进速度不同，因此路线选择将会受到环境因素制约.以避开所有减速区域只选择平坦路面为基础的传统算法并不适用于实际情况.改进算法中引入地形参数，可将量化后的路况信息数据写入地图模型，准确模拟真实环境下的机器人工作场景，并对机器人的越野能力、能否跨越障碍、越障耗时以及越障行为是否有利做出分析并选择最短路径.

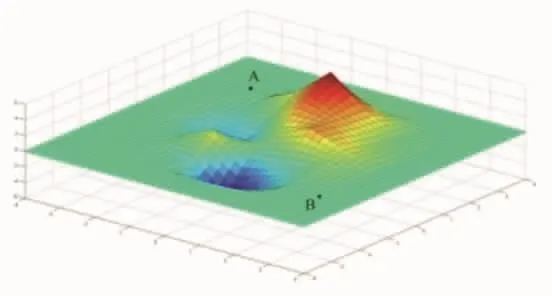
图4 复杂地形示意

处理带有地形参数的地图模型时，将整个地图看成一张平整但质地不均的宣纸，如果在源点处对宣纸进行浸水操作，由于水分子在宣纸上的扩散速率与宣纸各点密度成反比，最先扩散至终点的水分子运动路径为最优路径.

改进算法中的地图设计参考了宣纸浸水模型中对纸密度的定义：平坦路面对应宣纸中可正常湿水部分；大量消耗时间或难以通过的地形区域作为宣纸中不易湿水部分.从而更加有效的对应移动机器人通过平坦、山地、泥泞、涉水以及翻越障碍物等实际作业场景.

Dijkstra算法以层层扩展的形式展开搜索，只有当某层处理结束时才会扩展到下一层节点.因此改进算法将地形参数统一于扩展层次顺序中，即：地形参数控制某些节点在对应层扩展中暂时不扩展子节点并且将自己保留到下一层扩展Open表中某位置，直到该节点扩展滞后程度接近地形环境对机器人行进的时间消耗.

2.3 改进Dijkstra算法设计

在改进算法运行过程中，只需按顺序遍历Open表中节点，即利用广度优先方法对节点进行扩展即可.且改进算法设置源点集与终点集，支持区域目标或多区域多目标的路径规划.最优路径结果通过标号法将相应父节点与子节点连接后产生.改进算法运行步骤如下：

（1）给出源点集S及终点集T，并初始化Open表、Close表；

（2）将源点集S中所有节点加入Open表；

（3）取Open表中首个元素s1；

（4）选择与s1相邻且不在Close表中的所有节点s（n），将 s1标记为 s（n）的父节点；

（5）分析点s1处地形情况，判断是否应将点s1由Open表移入Close表中；

（6）将 s（n）加入 Open 表中；

（7）重复上述过程（3）到（6），直到任意 t∈T 进入Open表搜索停止；

（8）标记终点t父节点p1为路径点并不断重复此过程直到有p（n）∈S被标记为路径点时，路径标记完成；

（9）算法结束，记录数据.

改进算法运行流程如图5所示.

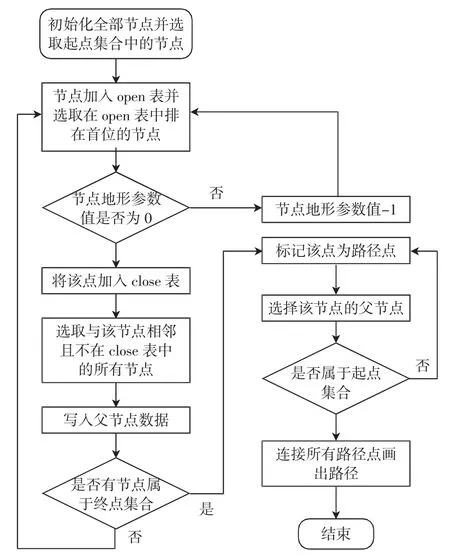
图5 改进算法流程

3 实验结果

改进Dijkstra算法采用蜂窝模型结构地图，剪除了运行过程中在Open表中的排序操作，对复杂地形下的障碍物区域进行分析，实现标记最优路径的同时提高了计算效率.

3.1 程序设计

为证明本文算法的有效性，在Windows 7系统下的Visual Studio 2013开发平台，通过MFC程序对传统Dijkstra算法与改进算法进行对比.程序流程如图6所示.

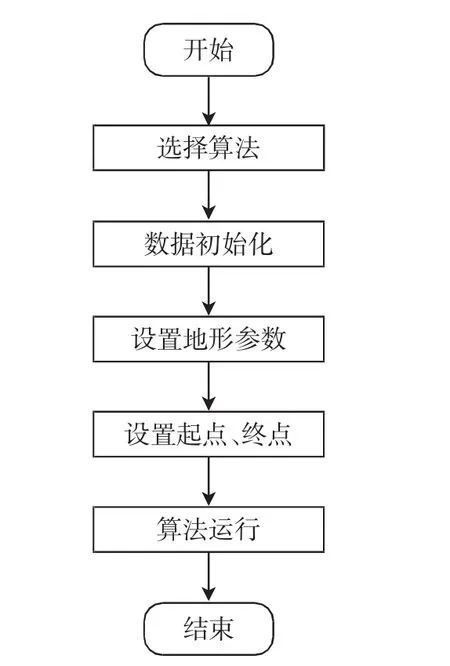
图6 程序流程

传统算法在无地形参数影响下的路径规划程序演示界面示意如图7所示.

图7 传统算法无地形分析示意

在不考虑地形参数影响下的路径规划示意图中，左侧方形区域为显示区，其中深色色块为障碍物区域，白色区域为平坦路面，红色线条为标记最优路径.

程序同时支持传统Dijkstra算法与改进算法的路径规划模拟仿真，并记录相应数据.

图8为改进算法在引入地形参数后对机器人路径进行规划的仿真程序界面，其中显示区域中白色为平坦路面，深色块区为地形条件较为复杂、机器人需低速通过的区域.且深色区块颜色越深表示机器人通过该区域时的难度越高，即时间消耗越大.

图8 改进算法程序仿真示意

3.2 结果分析

程序对传统DIjkstra算法、改进算法进行运行测试，并将结果与A*进行对比分析.算法仿真程序运行环境均为windows7操作系统、Intel Core i5 CPU、4G内存，在不同类型的障碍物比例情况下，几种算法仿真结果见表1.

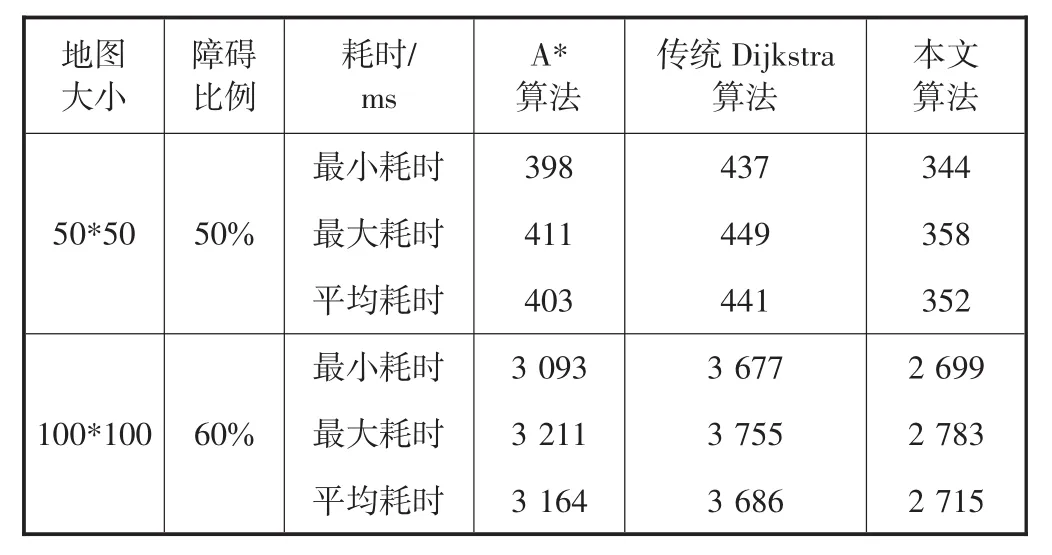
表1 算法运行速度对比

结果表明，在地形条件非常复杂、障碍物比例较大的情况下，A*算法处理节点数明显增加，启发式搜索优势减小.改进算法在复杂环境中搜索效率明显较高.

4 结语

对于机器人路径规划，本文提出一种蜂窝形地图模型对地图进行建模，并参考模拟宣纸浸水模型改进Dijkstra算法，引入地形参数信息分析，使移动机器人在复杂地形、危险地形以及多区域多目标地形条件下快速选择最优路径.对于抢险、消防等特种机器人路径规划问题的研究发展，具有一定实际意义.