基于A*算法在蜂巢栅格地图中的路径规划研究
陶 哲, 高跃飞, 郑天江, 李俊杰, 李保在
(1. 中北大学 机电工程学院, 山西 太原 030051; 2. 中国科学院大学 宁波材料技术与工程研究所, 浙江 宁波 315201;3. 山西北方机械制造有限责任公司, 山西 太原 030009)
0 引 言
移动机器人的路径规划问题是当前移动机器人领域所研究的热点问题[1], 其主要目标是在已知、 未知或者部分未知的环境中规划出从起始点到目标点的安全无碰撞路径.
针对已知的静态环境[2], 所用的全局路径规划算法通常有栅格法[3]、 RRT算法[4]、 A*算法[5]、 Dijkstra算法、 神经网络算法[6]、 遗传算法[7]、 蚁群算法[8]等等. 其中, 栅格法因结构简单, 计算量小的特点, 广泛应用于静态已知环境下的移动机器人路径规划问题, 并且取得了较好的效果. 但是, 传统栅格法在构建环境过程中使用的是正方形栅格, 会造成总路径过长, 绕行障碍物过于困难等问题, 不少学者对此做出了一些改进工作, 并取得了一定的成果. 谢昆霖等[9]对传统栅格地图进行了分区, 然后逐个区域规划路径, 最后进行路径拼接, 与直接进行规划的路径相比, 其规划的路径更具有优势. 分区是为了更细致地描述障碍物的信息, 将全局问题转化为子区域问题, 但最后的路径拼接过程不能保证一次性成功, 在一定程度上减小了路径规划效率. 王陈等[10]根据带球球员(移动机器人)以及防守球员(障碍物)的影响力对球场(传统栅格地图)进行了区域划分, 并为每个区域设置风险值(阈值), 然后进行路径规划, 路径长度与安全性比无分区的规划效果更好. 区域划分、 设置阈值都是为了更好地描述障碍物信息, 但却没有在区域形状、 大小及数量上进行分析和阐述, 不能保障所得到的路径是最优解. 曾辰等[11]提出一种蜂巢栅格方法对环境建模, 采用蚁群算法对移动机器人在复杂环境下进行路径规划, 对比传统栅格方法得到了较好的路径. 姚成信等[12]将树生长模拟算法(TGSA)引入蜂巢栅格环境地图中, 规划路径的效率相比于传统栅格地图更加有优势. 武凌宇[13]通过对蜂巢栅格地图重新进行编码, 提高了的遗传-蚁群的算法效率. 尽管以上研究都使用蜂巢栅格环境地图来增加路径规划的效率, 但其规划仅仅基于正六边形结构, 并未考虑其它结构, 规划出的路径并不是最优的.
本文结合前人的研究成果, 对栅格地图采用不同栅格类型进行表示与构建等方面进行研究, 并采用全局路径规划算法进行了验证. 结果表明, 蜂巢栅格在栅格地图中的使用会减少路径规划的迭代次数, 节省路径规划的时长, 减少路径的总长, 可提高路径规划的效率.
1 模型构建
1.1 环境建模
栅格法是最常用的环境建模方法, 在室内和室外的环境建模中均被广泛应用, 其原理是将整个地图的二维环境空间进行细化, 形成一组网格, 网格包含人为指定的信息, 这些含有信息的网格被称为环境单元. 单元格中含有0、 1的二值信息, 1表示该单元格与障碍物相交, 0表示该单元格不与障碍物相交. 用这种方式将整个环境进行抽象建模, 并采用相应的路径搜索方法在该空间内进行搜索.
1.2 栅格构建
1.2.1 传统栅格构建
通过激光扫描得到环境的全局地图, 在地图中设定坐标原点o, 并建立坐标系xoy, 规定水平向右为x轴正方向, 竖直向上为y轴正方向. 根据移动机器人自身的大小规划出对应的单位栅格, 设定坐标轴上的单位长度为单位栅格大小, 细化后即可形成正方形栅格地图, 并对应实际环境将栅格分为白色栅格和黑色栅格. 如图 1 所示, 白色栅格为自由栅格, 移动机器人可自由通过; 黑色栅格为障碍物栅格, 该栅格部分或者全部有障碍物占据, 移动机器人不可通过.

图 1 传统栅格地图Fig.1 Traditional grid map
1.2.2 菱形栅格构建
菱形栅格构建与传统栅格构建相同, 都需要通过激光数据获取到全局的环境信息, 确定障碍物的相对位置. 为了构建菱形栅格, 以内角为60°的菱形为单个栅格为例, 如图 2 所示, 将直角坐标系“挤压”为斜60°坐标系, 即x轴和y轴分别位于菱形内角两边, 并按照先前设定的菱形栅格大小进行平铺, 使其充满整个全局地图. 然后从原点位置开始对实际环境中的障碍物进行编码和标记, 即可得到栅格地图中障碍物和自由空间的位置. 最后, 经过扩张得到整个环境的菱形栅格地图, 如图 3 所示.

图 2 直角坐标系“挤压”过程Fig.2 Cartesian coordinate system “squeeze” process

图 3 内角60°的菱形栅格地图Fig.3 Diamond-shaped grid map with an inner angle of 60 °
1.2.3 蜂巢栅格构建
正六边形栅格俗称蜂巢栅格, 其构建方法可分为3步, 如图 4 所示.
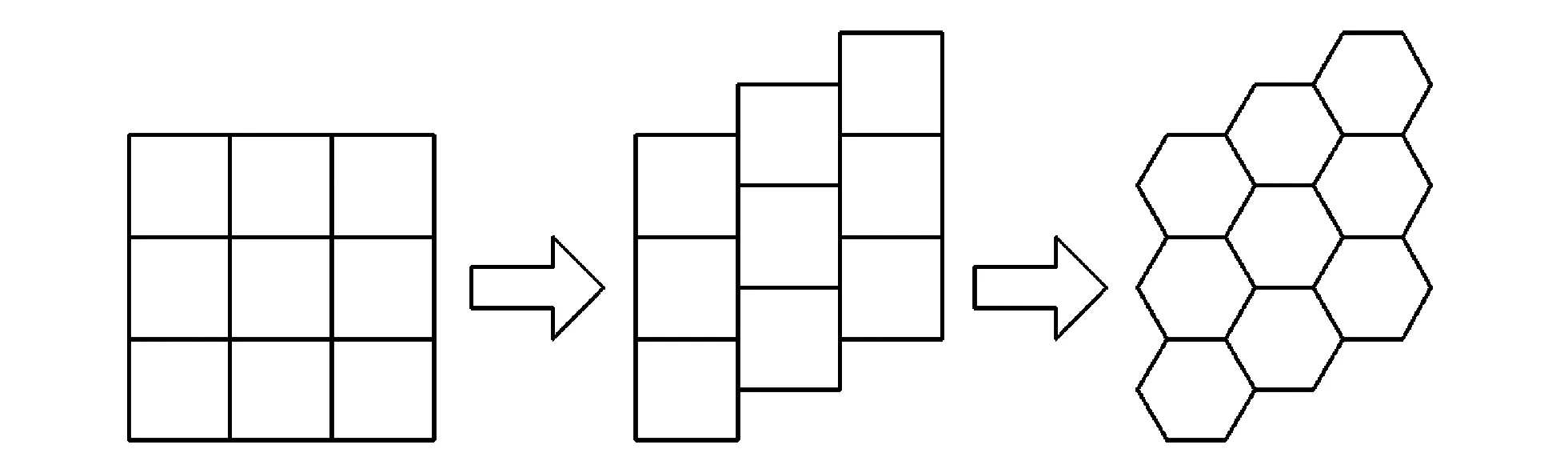
图 4 “蜂巢栅格”转化过程Fig.4 “Honeycomb grid” transformation process
第1步, 将传统栅格中每列逐个进行半个栅格长度的偏移; 第2步, 将每个传统栅格的两边进行打断, 并在中间部分弯曲, 即形成六边形栅格; 第3步, 将形成的六边形栅格大小和形状进行调整, 形成单位长度的蜂巢栅格, 并对全局地图进行覆盖, 形成整个蜂巢栅格地图. 同理也可以将传统栅格中每行进行一定的偏移, 得到蜂巢栅格地图.
通过以上的行、 列两种方式偏移, 形成图 5 所示的两种蜂巢栅格排布方式, 分别为尖顶排布和平顶排布.
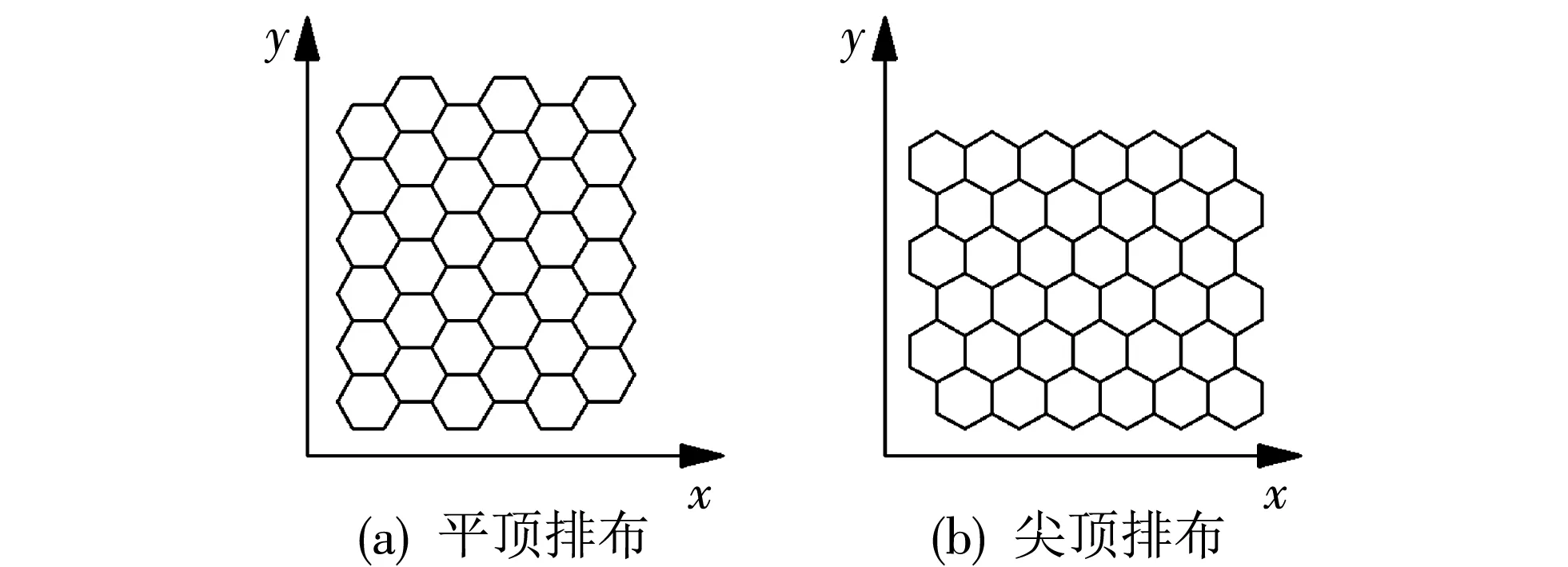
图 5 蜂巢栅格排布图Fig.5 Honeycomb grid layout
由于每个蜂巢栅格都有6个相邻的栅格, 即移动机器人在每个栅格的位置都会存在6个预运动方向, 为了更好地描述运动, 采用图 6 描述栅格位置的坐标系. 图 6 的三系数坐标系虽然在栅格构建时会提供很大的便利, 却在对实际环境进行描述时, 造成了较大的困扰. 假如地图环境轮廓约为正方形、 长方形、 圆形等类似图形, 用此坐标系对其进行描述, 存储空间会产生极大的浪费, 尤其是在x轴与水平线的夹角部分; 假如地图环境轮廓约为平行四边形、 长椭圆等类似图形, 用此坐标系可更加贴合实际环境, 表达较为合适. 而在实际仿真环境下, 基本环境轮廓为正方形或长方形, 为了避免该坐标系对地图环境空间存储造成很大的占据及浪费, 为此进行了改进.

图 6 蜂巢栅格二维三系数坐标系Fig.6 Honeycomb grid two-dimensional three-factor coordinate system
蜂巢栅格地图的尖顶排布如图 7 所示, 转换为传统xoy坐标系, 可以为单、 双行进行位置标记, 即奇数行右偏置或偶数行右偏置.

图 7 尖顶排布坐标标记Fig.7 Coordinate markers on pointy top
蜂巢栅格地图的平顶排布如图 8 所示, 转换为传统xoy坐标系, 可以为单、 双列进行位置标记, 即奇数列下偏置或偶数列下偏置.

图 8 平顶排布坐标标记Fig.8 Coordinate markers on flat top
以上4种方式在构建蜂巢栅格地图的原理相通, 最终表达类似, 所以选择以偶数列下偏置为例进行栅格标记的转换讨论, 转换结果如图 9 所示.
三系数斜坐标系中表示每个栅格位置为(x,y,z), 经过式(1), 每个栅格的位置在直角坐标系中可表示为(x′,y′).
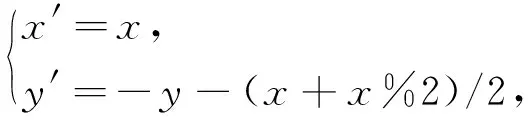
(1)
式中:x′为蜂巢栅格的列数;y′为蜂巢栅格的行数; %表示取余.
通过以上转化, 就能以任意蜂巢栅格的中心为坐标原点, 建立出二维xoy直角坐标系, 即可便捷地描述出各个障碍物和自由空间的位置, 并且更适合描述形状规则的地图环境, 大大节约了地图信息的储存.

图 9 坐标系转换结果图Fig.9 Plot of coordinate system transformation
1.2.4 三角形栅格构建
针对三角形栅格地图, 本文以正三角形栅格为例进行构建, 可以将正三角形栅格的构建看成60°菱形栅格的细化, 过程如图 10 所示.

图 10 三角形栅格构建过程Fig.10 Triangular grid construction process
首先, 对传统的正方形栅格进行压缩, 使其变成60°菱形栅格地图; 其次, 将每个60°菱形栅格短对角线相连, 使1个菱形划分为2个正三角形; 然后用划分成的正三角形对环境进行扩充, 使其充满整个环境地图, 并且对环境地图中的障碍物位置信息进行描述; 最后即得到正三角形栅格地图所描述的地图环境.
反过来看, 正三角形栅格地图中的每个顶点都会连接6个正三角形, 恰好这6个三角形拼成了1个正六边形, 从而可以认为正三角形栅格地图也是正六边形栅格地图的细化.
由此可知, 这些栅格地图从构建方法上都存在着密切的关系, 下文将对以上栅格进行分析, 从而找出最适合构建栅格地图的栅格类型.
2 栅格分析
2.1 路径规划策略分析
传统栅格地图的栅格形状为正方形, 大小与移动机器人大小相对应, 一般采样的规划策略为四叉树和八叉树. 四叉树策略规划的路径是经过每个栅格中心点的, 如图 11 所示; 而八叉树策略规划的路径不仅会经过每个栅格中心点, 而且会经过每个栅格的顶点, 如图 12 所示. 各种栅格不同策略对比如表 1 所示.

图 11 各种栅格在四叉树策略下的运动方向Fig.11 Movement direction of various grids under quadtree strategy

图 12 各种栅格在八叉树策略下的运动方向Fig.12 Movement direction of various grids under octree strategy
表 1 策略栅格对比
Tab.1 Strategy grid comparison
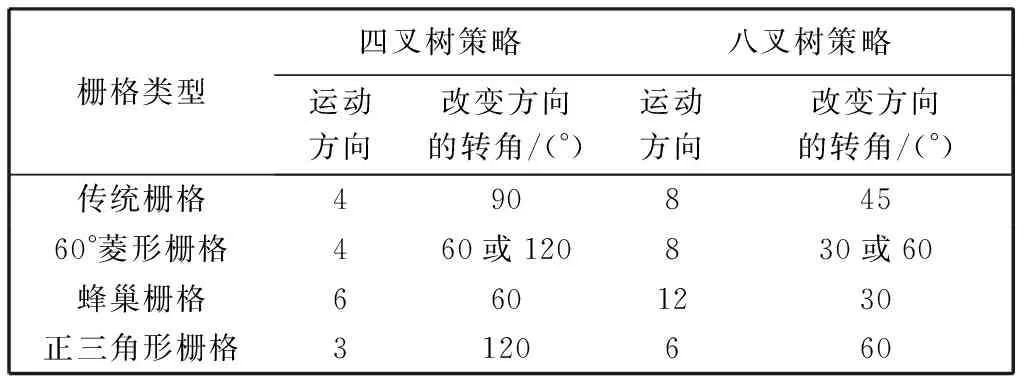
栅格类型四叉树策略八叉树策略运动方向改变方向的转角/(°)运动方向改变方向的转角/(°)传统栅格49084560°菱形栅格460或120830或60蜂巢栅格6601230正三角形栅格3120660
由表 1 可知, 虽然在八叉树策略下移动机器人在栅格的运动方向得到了增加, 改变方向的转角也大大减少, 可以使规划的路径总长较小, 但由图 12 可知, 当移动机器人在对角线方向行驶时, 会产生对相邻两个栅格的占据, 假如相邻栅格恰好是障碍物, 则很大概率会与其发生碰撞, 安全性难以保障. 因此, 这样规划出的路径会伴随很高的危险性, 使得地图的保守性较大. 由于在使用栅格地图路径规划的过程中, 安全性是第一选择, 加之八叉树策略目前只能通过栅格的细化提高安全性能, 大大增加了栅格的计算数量和规划的运行时间, 所以, 现阶段为保证最大安全性, 选择四叉树策略规划路径比较合适.
在四叉树策略条件下, 通过表 1 可知, 蜂巢栅格相对于其他类型的栅格, 拥有最多的运动方向和较小的改变方向转角, 使其不仅适用于全向移动机器人的运动, 而且可增加规划路径的灵活性, 减少规划路径的总长. 路径转向角越小, 可缓解移动机器人运动的惯性加速度问题, 在一定程度上提高了运动的准确性和运动过程中的安全性, 为之后的路径平滑处理提供了很好的基础.
2.2 栅格占据分析
栅格地图的每个单位栅格都是与移动机器人的外轮廓尺寸相对应的. 假定移动机器人是一个半径为α的圆, 则对应的不同类型的单位栅格如图 13 所示, 占据比公式为

(2)

图 13 不同类型栅格的栅格占据比Fig.13 Occupancy ratio of different types of grids
由图 13 可知, 蜂巢栅格的栅格占据比最大, 为0.906 9, 正三角形栅格的栅格占据比最小, 为 0.604 6, 而传统栅格的栅格占据比为0.785 4. 相比较之下, 在同样尺寸大小的地图中, 蜂巢栅格对地图面积的利用率最高, 平铺栅格数量最多, 即可更加细致地描述地图环境信息.
2.3 路径比分析
在栅格地图路径规划过程中, 最常见的情况是当前运动方向存在障碍物, 此时移动机器人会沿轨迹选择绕行, 完全绕过障碍物后继续向目标点前进. 为了更有效率地规划路径, 绕障碍物的路径比成了重要的参考标准. 图 14 为不同类型栅格情况下绕障碍物的路径图, 表 2 为各类型栅格路径比对比.
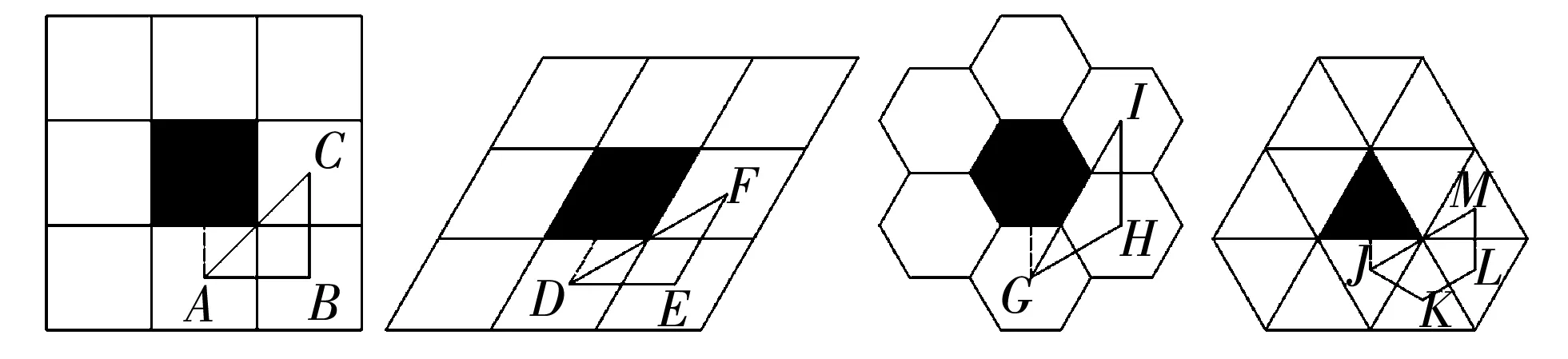
图 14 不同类型栅格绕障图Fig.14 Different types of grid obstacle maps
表 2 不同类型栅格路径比
Tab.2 Different types of grid path ratio

路径参数正方形栅格60°菱形栅格蜂巢栅格正三角形栅格路径比(公式)AB+BCACDE+DFDFGH+HIGIJK+KL+LMJM路径比值1.414 21.154 71.154 71.5
由表 2 可知, 传统栅格地图的路径比为1.414 2, 60°菱形栅格和蜂巢栅格的路径比都为1.154 7, 正三角形栅格的路径比为1.5. 路径比越小, 移动机器人行走路径的总长和路径规划运行时间就越少, 所以60°菱形栅格和蜂巢栅格的路径在越障方面比传统栅格的路径更加优秀.
3 仿真实验分析
为了验证蜂巢栅格相对于传统栅格在全局路径规划方面的优势, 本文采用MATLAB软件进行了仿真. 实验地图环境尺寸大小为20 m×20 m, 分别建立在传统栅格构建的二维平面、 蜂巢栅格构建的二维平面和普通的障碍物地图中. 图 15~图 20 中, 左下角正方形表示移动机器人的起始位置, 右上角正方形表示移动机器人的目标位置, 黑色部分为障碍物(已进行膨胀处理).
地图环境a(图15)和地图环境b(图18)分别代表两种不同类型的环境, 在传统栅格下的表示分别为图 16 和图 19, 蜂巢栅格下的表示分别为图 17 和图 20. 地图环境a表示具有一定数量的较大型障碍物的场景, 与大面积较空旷的室外环境相类似; 地图环境b表示具有多数量大小障碍物的复杂场景, 与复杂的室内测试环境相类似.

图 15 地图aFig.15 Map a

图 16 地图环境a在传统栅格下的表示Fig.16 Representation of map a in traditional grid
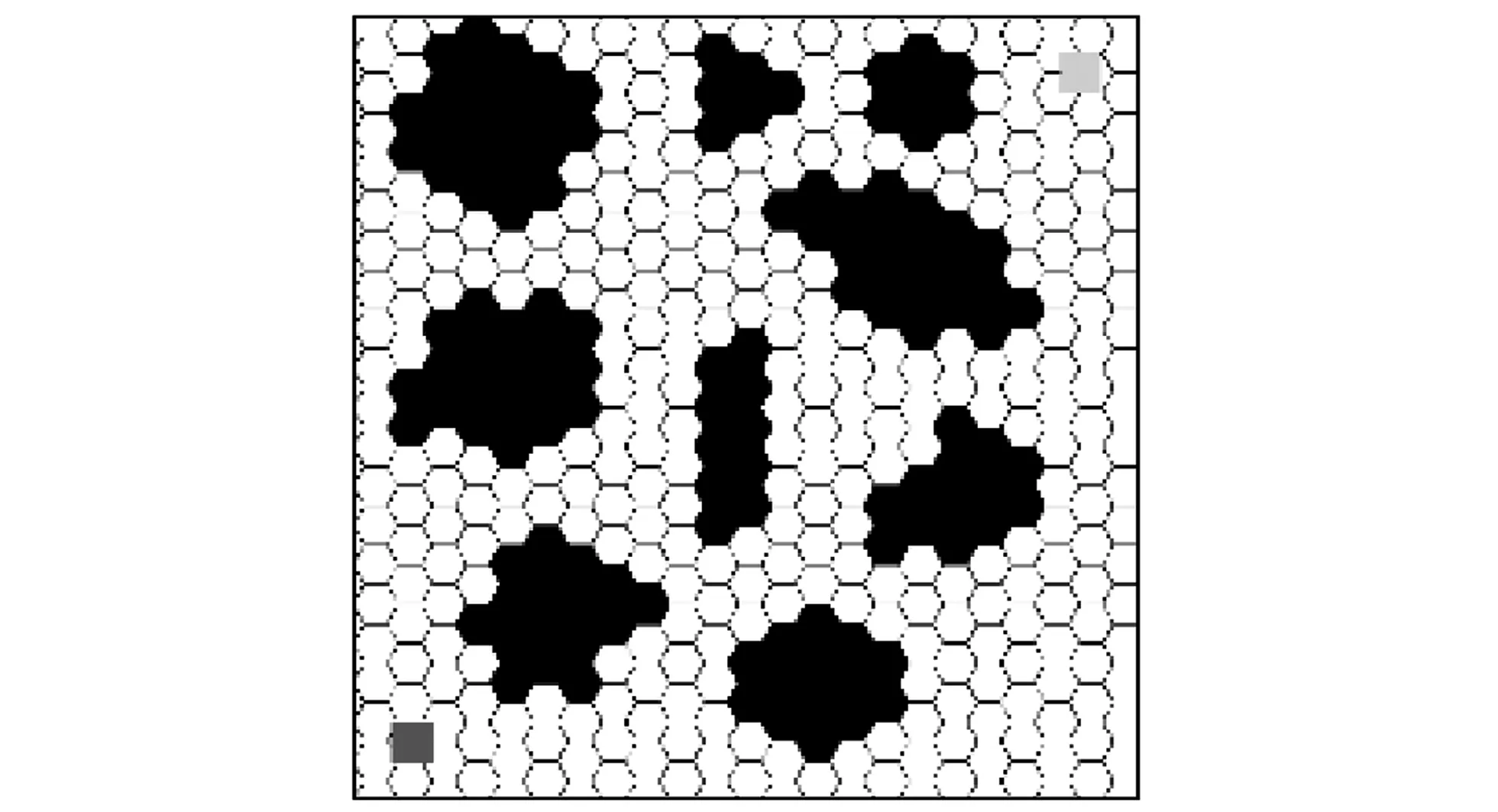
图 17 地图环境a在蜂巢栅格下的表示Fig.17 Representation of map a in honeycomb grid

图 18 地图 bFig.18 Map b
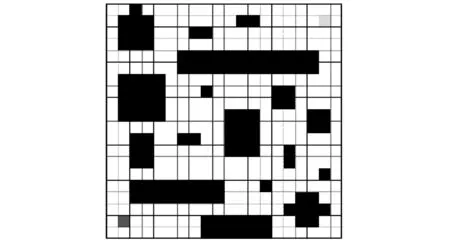
图 19 地图环境b在蜂巢栅格下的表示Fig.19 Representation of map b in honeycomb grid
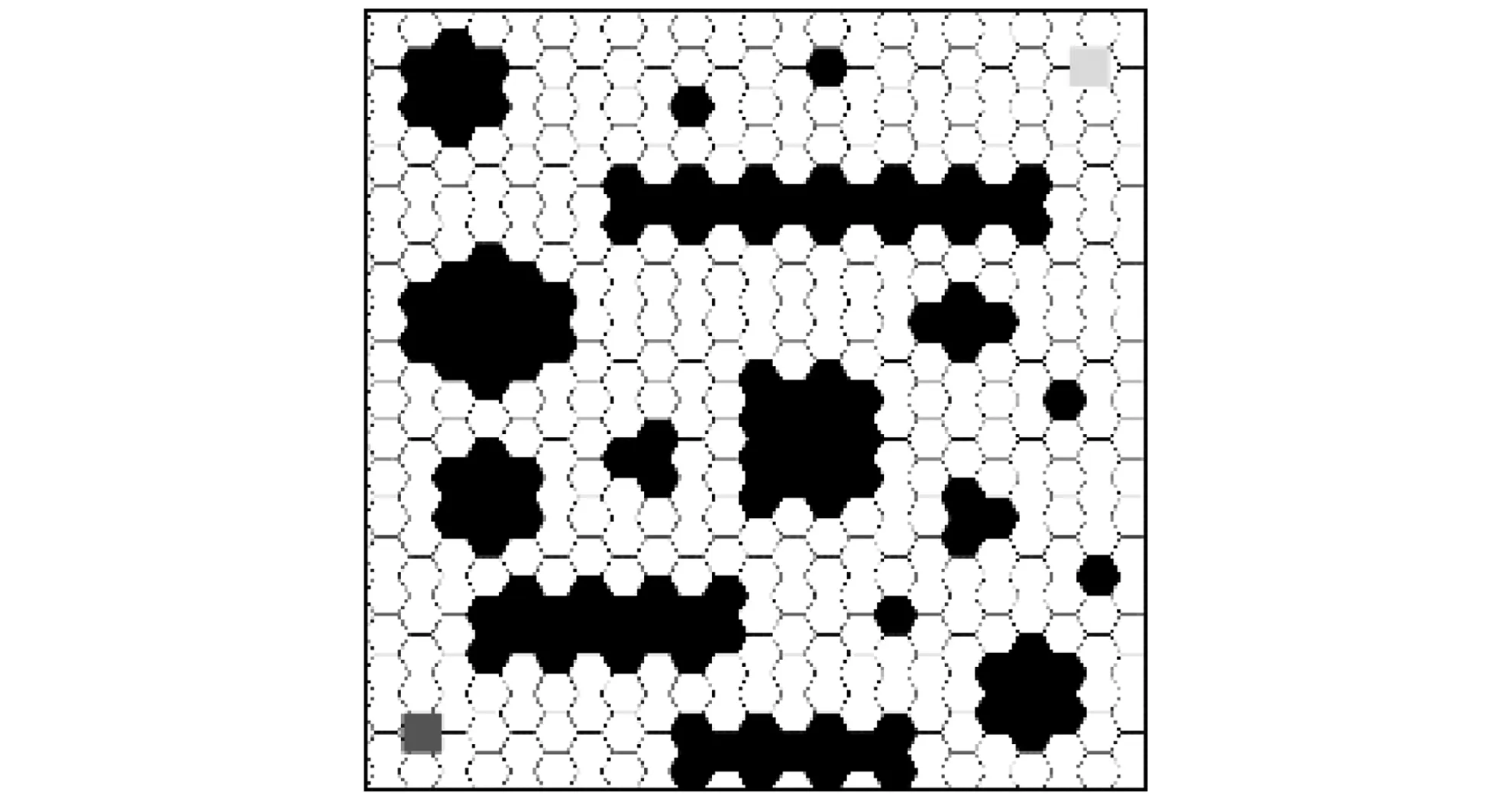
图 20 地图环境b在蜂巢栅格下的表示Fig.20 Representation of Map b in honeycomb grid
本文主要针对全局路径规划算法A*算法、 Dijkstra算法和BFS算法进行研究.
相比于其他两种算法, A*算法的代价函数带有问题自身的启发性信息, 因此, A*算法又称启发式搜索算法, 其搜索流程如下.
A*算法在进行搜索之前(已知起始点), 首先创建启发式函数
f(n)=g(n)+h(n),
(3)
式中:f(n)为起点到终点的总代价;g(n)为从起点到某个中间点的代价;h(n)为从上述中间点到终点的代价. 其次创建两个数据表, open表和close表. 其中, open表存放待搜索的节点, close表存放计算后代价最小的节点. A*算法核心是从open表中选择最优的节点移到close表中, 然后将未探索节点放入open表中, 重复操作选取最优节点(f值最小的点), 直到到达目标或者open表为空. 此时, close表中的节点可以将起始点串联起来, 这些节点的排序即为最优路径或次最优路径.
表 3 为以上3种传统算法的分析对比.

表 3 传统全局路径规划算法分析
通过以上分析, 在仅有单一目标点时, A*算法更适合于栅格地图的路径规划, 即实验仿真采用A*算法进行栅格地图的验证. 在地图a的环境中, 仿真结果如图 21、 图 22 所示; 在地图b环境中, 仿真结果如图 23、 图 24 所示. 仿真结果的总结对比如表 4 所示.

图 21 地图环境a在传统栅格下的规划路径Fig.21 Map a planned path under traditional grid

图 22 地体环境a在蜂巢栅格下的路径规划Fig.22 Map a planned path under honeycomb grid

图 23 地图环境b在传统栅格下的规划路径Fig.23 Map b planned path under traditional grid

图 24 地体环境b在蜂巢栅格下的路径规划Fig.24 Map b planned path under honeycomb grid
表 4 仿真结果对比
Tab.4 Comparison of simulation results
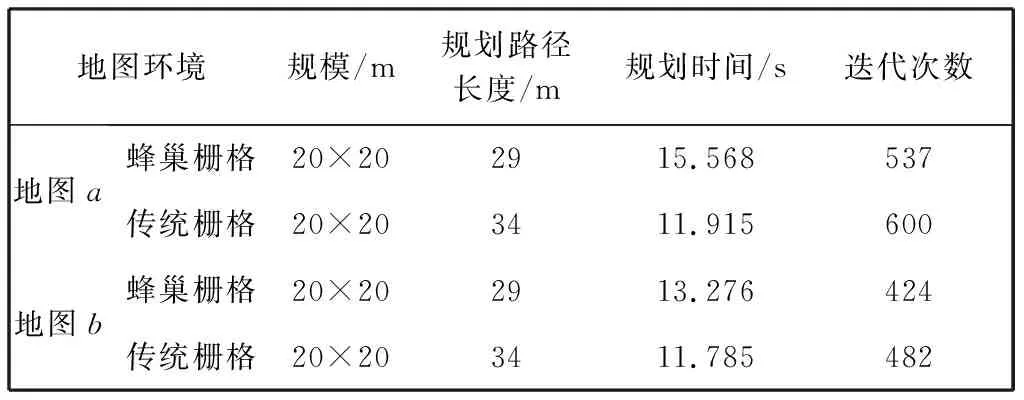
地图环境规模/m规划路径长度/m规划时间/s迭代次数地图a蜂巢栅格20×202915.568537传统栅格20×203411.915600地图b蜂巢栅格20×202913.276424传统栅格20×203411.785482
通过以上仿真分析可以看出, 同样基于启发式的A*算法, 在具有一定数量较大障碍物的地图a中, 蜂巢栅格地图下规划的路径总长比传统栅格地图下规划的路径总长少14.7%, 消耗时间增加了30.8%, 迭代次数减少了10.5%; 在较大障碍物之中具有一定数量的小障碍物的地图b中, 蜂巢栅格地图下规划的路径总长比传统栅格地图下规划的路径总长少14.7%, 消耗时间增加了12.6%, 迭代次数减少了12%. 因此, 在相同环境和算法的情况下, 蜂巢栅格的使用相对于传统栅格会大大提高路径规划的效率和规划路径总长. 通过以上实验可以发现, 但凡起始点和目标点之间客观存在一条通道, 不管环境多复杂, 运用蜂巢栅格地图都可以搜寻到一条安全的路径.
4 结 论
为了解决全局路径规划算法在传统正方形栅格地图中规划效率较低的问题, 本文从栅格地图的构建、 信息编码、 规划策略等方面对不同种类栅格的栅格地图进行了分析对比, 得出了蜂巢栅格的栅格地图比传统正方形栅格的栅格地图在全局路径规划方面更具有优越性. 文中以A*算法、 Dijkstra算法和BFS算法这3种传统路径规划为示例, 经过对比分析, 最终以A*算法进行最后的实验仿真. 实验结果表明, 蜂巢栅格地图在地图信息表示、 路径规划效率、 路径规划总长和迭代次数等方面相对于传统栅格表现更加优秀.

