衰落相关信道近似算法及其Massive MIMO系统分析∗

周杰，邹士娇，陈 珍，菊池久和

(1.南京信息工程大学气象探测与信息处理重点实验室，南京210044；2.日本国立新泻大学工学部电气电子工学科，新泻950-2181)

0 引言

5G是面向2020年以后移动通信需求而发展的新一代移动通信系统，它将与其他无线移动通信系统紧密结合，构成新一代全覆盖的移动信息网络.那时，无线数据业务流量将会比现在增长数百倍，对于人机混合通信、物联网以及其他创新应用，将新增百亿互联网通信设备，将产生前所未有的多样性要求与各种特殊移动应用场景，从而形成无所不在的移动信息网络.其数据传输无线信道极大程度地依赖于其工作的环境，具有多频段与超密集的多种异构网络，将使未来移动网络可能工作在不同的频段和蜂房小区.因此，将存在大量不同种类需要表述特征的信道，且多以高维度信道建模与估计为主要研究对象.这些研究对象已成为未来移动通信领域亟待解决的关键技术问题，受到了全世界各国科学家的关注[1−6].另外过去的研究证明MIMO(Multiple Input and Multiple Output)无线传输技术能够充分挖掘、利用空间资源，提高频谱利用率和功率效率.其MIMO多天线技术已作为提高系统频谱效率和传输可靠性的有效手段，而应用于4G/3G、LTE、LET-A以及WLAN等系统中.在未来5G系统中，传统的MIMO技术已不能满足呈指数上涨的无线数据传输需求.BELL实验室的T.L.Marzetta在2010年提出了大规模MIMO(Massive MIMO或Large Scale MIMO)的概念，需要我们去深入研究信道场景的“适宜”以及各种“限制”条件下的MIMO多天线技术，建立起与之相关的信道模型、估计理论及其信号检测方法等，所有研究具有极其重要的意义[2,3].

过去的大量研究表明,MIMO多天线系统的信道容量取决于其多径信道矩阵的秩,而信道矩阵的秩依赖于天线端口处信号的空间衰落相关性SFC(Spatial Fading Correlation),所以MIMO多天线阵元间信号SFC是决定信道容量的关键因素.文献[12-16]利用较为实际的几何信道模型仿真和分析了MIMO ULA(Uniform Linear Array)和UCA(Uniform Circular Array)多天线信号SFC以及信道容量；文献[8]对室内微小区移动通信环境的多普勒效应与信道参数进行了分析,但是计算仿真方法复杂，在大规模MIMO天线阵列条件下可能计算效率较低.另外，在对真实传输系统进行仿真时,其信道衰落参数主要取决于波达信号PAS(Power Azimuth Spectrum)和多天线阵列收发模式.因此，本文深入研究了空间衰落信道模型及其近似算法，从而分析Massive MIMO系统性能和算法效能.首先导出在典型PAS下的SFC函数的闭合表达式，研究在小角度扩展时的近似算法以及评估其计算效能，建立MIMO多天线接收模型和分析其系统性能.研究揭示了其信道特征的诸多关键因素，阐明阵元接收信号强度变化、阵元衰落信号相关性和信道矩阵分布特征.通过理论计算和仿真实验得出近似计算法在特定条件下具有很好的拟合度，定量分析了近似算法在对MIMO多天线系统分析时的适用性和计算效率.通过理论计算得出近似计算法在特定条件下具有很好的拟合度,并能极大地减低计算复杂性而提高分析和仿真系统的效率.

1 信道系统模型与Massive MIMO

1.1 统计信道模型

准确认知无线通信场景的传播特性是MIMO多天线系统设计、算法优化和网络构建的重要基础.多年来针对蜂窝移动通信系统，用于传统的MIMO信道建模的方法主要有确定性衰落信道建模方法和基于统计特征的建模方法.由于无线通信系统工作场景非常多，具体有多维信道模型、电磁模型、基于几何学模型以及经验模型等等.这些信道模型方案中，已出现系列标准化模型，如IEEE802.11TGn、IEEE802.16d/e和3GPP/3GPP2空间信道模型等.其中著名3GPP的MIMO多天线信道模型就是基于空时衰落相关特性的统计信道模型.在图1所示的信道模型建模流程中，一般直接假设各“簇”的反射波达信号的功率谱PAS，根据波达信号角度扩展及其AOA/EOA分布，再利用信号矢量模型导出不同天线阵列配置以及角度扩展下的信道空间衰落相关特性、时间相关特性以及空/时联合相关特性.再对获取信道相关参数矩阵以及采用Kronecker乘积和矩阵Chelosky分解，求得信道衰落矩阵H从而建立起基于统计的信道模型.

近期，无线通信领域从传统的MIMO技术到近期的Massive MIMO新兴技术，它们在通信理论上还没有完善，Massive MIMO的各种技术还在继续发展.另外，从过去传统MIMO到Massive MIMO的演变和应用中,会出现“准Massive MIMO”阵列，针对此类问题，最需要解决的问题有：(1)如图2所示的由于Massive MIMO多天线阵列规模较大，到达不同阵元的电波呈现球面波特性；(2)如图2所示的由于天线阵列尺寸较大，在诸阵元观察到的信道的衰落特征具有非平稳特性问题；(2)阵元衰落信号相关性计算复杂性与效率问题.如图2所示的Massive MIMO，可能不是所有的簇都能在所有阵元上观测到，因此从阵列最远端到最近端来看，诸阵元将经历完全不同的大小尺度的信号衰落，可能造成信道统计衰落特征急剧变化.过去很多研究测量结果阐明“余弦形”和“钟形角度功率谱PAS”较为符合实际场景的测量数据，因此可考虑“簇”的反射波达信号PAS在均匀分布、截断高斯分布、拉氏分布等多边带功率方位谱时，导出Massive MIMO的相关衰落信道矩阵，研究各子信道的正交性以及不同“簇”分布对衰落相关性的影响.因此，波达信号PAS分布可为均匀分布，则其分布函数为[6−10]：

其中2∆为波达信号到达角AOA的扩展范围.功率谱PAS也可假设PAS分布为高斯分布，其分布函数为：

其中Cg为高斯分布的归一化因子，另一类典型PAS分布为拉氏分布，其分布函数为：

图1 MIMO空间衰落信道建模流程图

图2 Massive MIMO与波达信号PAS示意图

1.2 Massive MIMO模型

在现代移动通信发展过程中，在非额外增加信道频带资源的情况下由于MIMO具有利用多径效应极大地提高通信系统容量优势，所以近年得到了广泛的应用，许多高速传输系统的国际标准都是建立在MIMO之上的.随信道频段的不断上升与天线尺寸减小，为进一步提高数据传输速率，提出了Massive MIMO系统的技术模式，它将会是下一代移动通信系统的关键技术之一.现国际上主要有3个研究团队开展相关研究，分别是瑞典Link Ping大学Larsson教授、印度科学理工学院Chockakingam教授和美国Rice大学Marzetta教授团队，他们分别从信号处理关键技术、性能分析、天线设计和原型机等方面对Massive MIMO相关技术展开了卓有成效的研究[19,20].

2010年底贝尔实验室科学家提出的Massive MIMO大规模技术，近期并有望未来成为2020年未来5G宽带通信的物理层核心技术.相对传统的点对点MIMO技术，Massive MIMO主要在于采用多副(一般超过100副)天线来配置，天线配置阵列如图3所示，这样可以进一步挖掘空间增益，以提高系统传输容量.但是阵元配置多少会受到环境影响和需求，因此也存在“准Massive MIMO”，使得使用的天线数量相对较少，如有研究中使用了12×15、16×16线阵列开展了2GHz频段的室外信道测量，分析到达角AOA和Doppler特征等、以及使用64×21的天线阵列情况.在Massive MIMO系统中，有许多方面影响系统的总性能，其中信号间的衰落相关性和天线间互耦效应是两个比较重要的因素.本研究将依据图1所示的统计信道建模流程，研究和探讨Massive MIMO信号衰落相关性，提出Massive MIMO多天线系统，利用空间分集技术极大地提高系统空间利用率，如阵元数量与阵元间距.无论阵列如何配置，任意两阵元间的SFC均可看作线阵列LA(Linear Array)阵元间的SFC，它是组成任意配置阵列的基础.一般地LA阵列的导向矢量为[12−14]：

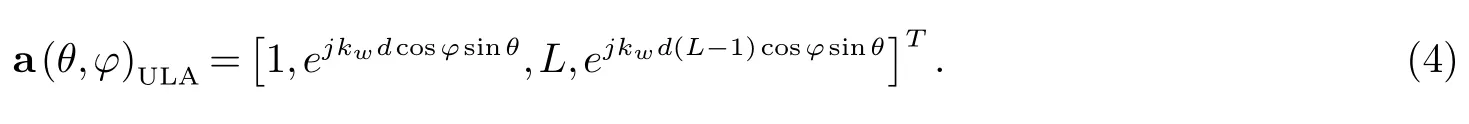
式中L为ULA天线的阵元总数，kw=2π/λ，λ为波长.由衰落相关性定义可得阵元m和n间的SFC函数为：

式中E[•]为数学期望，(•)∗为共轭，hm、hn为阵元m、n的信道脉冲响应分别为阵元m和n信道脉冲响应的平均值，am(θ,φ)、an(θ,φ)分别为阵元m和n的导向矢量，p(θ,φ)为多径分量到达角的联合PDF 分布.当方位角和仰角相互独立时，有p(θ,φ)=p(θ)p(φ).由于三维空间域的计算和仿真相当复杂，自然界通信终端在三维空间中φ均较小，所以多数研究通常考虑二维空间域[1−6]情况，即取p(φ)=1，其Massive MIMO阵列具体接收信号原理图如图4所示.在图4中，考虑Massive MIMO多天线阵列的任意两两阵元，在到达阵列的平面波信号角度为θ，在两阵元接收端的信号可表示s1(t)=m(t)和s1(t)=m(t)exp{j2πd/λsin(θ)}.若m(t)的幂为1即假设归一化信号功率，E[•]部分即可简化，则可以得到E{s1(t)(t)}=exp{j2πd/λsin(θ)}.针对LA阵列其d为两参考阵元天线之间的间距，通过式(5)可得阵列两阵元m和n间的信号衰落SFC为[13−16]：

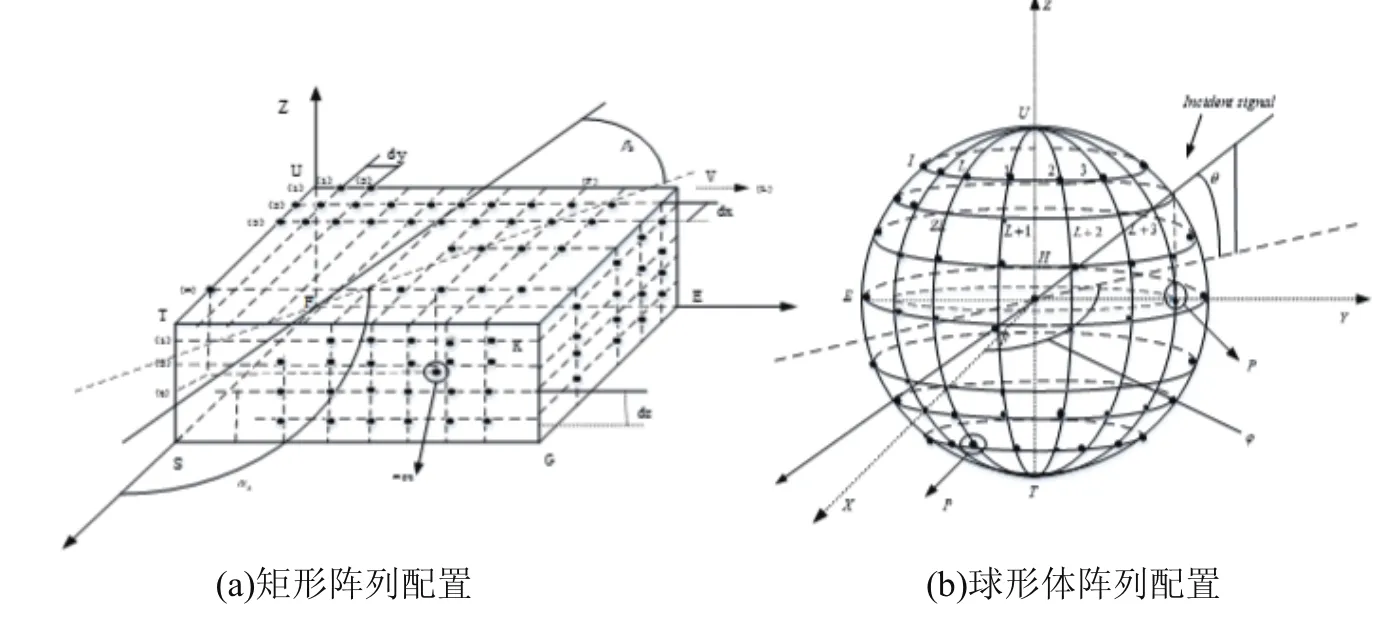
图3 Massive MIMO多种阵列配置模型

2 Massive MIMO阵元间衰落相关性及其近似算法

如上所述，在三维空间域分析天线阵元接收信号信道相关性，最终转变成方位面和仰角面的分析.许多文献研究中基于分析的难度，仅考虑了方位面和仰角面的波达信号PAS为相互独立的功率谱分布.因此为简化分析，本文仅考虑二维方位平面波达信号PAS和天线在方位角平面的旋转对Massive MIMO多天线阵列性能的影响.Massive MIMO LA阵列与CA阵列模型及其波达信号参数，如图4所示.下面分别就LA和CA阵元导出其两两阵元间信号衰落相关性SFC.

图4 二维空间域Massive MIMO阵列与波达信号关系

2.1 Massive MIMO LA阵列两参考阵元m和n间SFC

如1.1节所述波达信号功率谱PAS可为高斯、拉氏和均匀分布.若假设功率谱分布为均匀分布，将分布函数(1)代入式(6)，可得在均匀分布下SFC理论式为[10−11]：

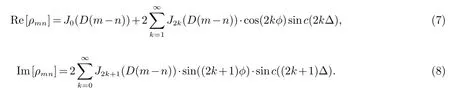
式中，参数D=2πd/λ，λ为信号波长.当∆较小时，可得到理论近似式：

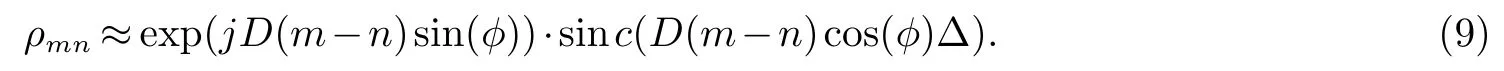
若假设功率谱分布为高斯分布[17−19]，将分布函数(2)代入到式(6)中得衰落信号相关性式为：

同理，在参数σ较小时可得到衰落信号相关性近似式为：

若假设功率谱分布为拉普拉斯分布，将式(3)代入到式(6)中得衰落信号相关性式为[14−16]：

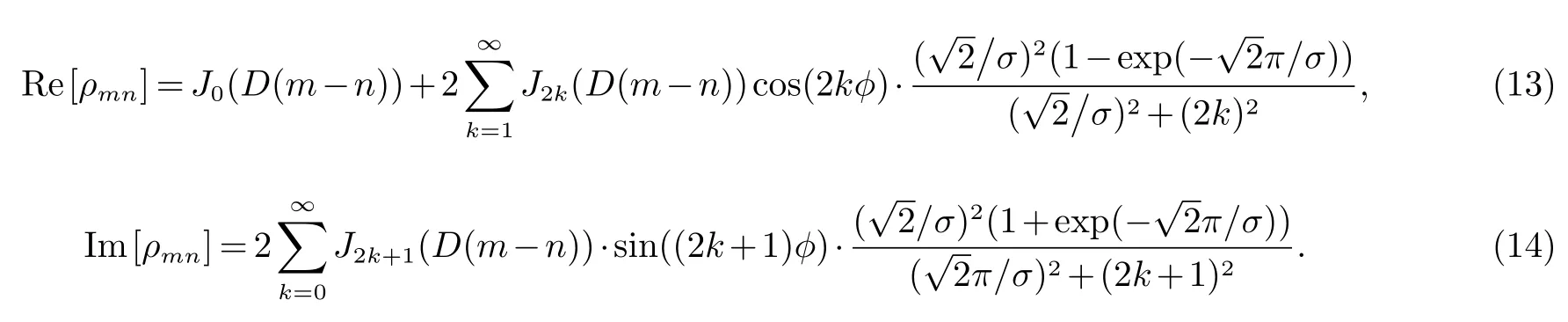
当参数σ较小时，则衰落信号相关性近似式为：

2.2 Massive MIMO CA阵列两参考阵元m和n间SFC

如图4(b)所示，在Massive MIMO CA阵元m和n的圆形天线阵列中，半径为R，第m天线阵列单元与水平方向夹角为Ψm，在功率谱为均匀分布时CA阵列的阵元m和n之间的衰落信号相关性SFC为[13−15]：

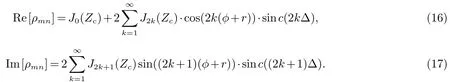
及其近似理论式为：

在功率谱为高斯分布时CA阵列的阵元m和n间SFC为：

其近似理论值为：

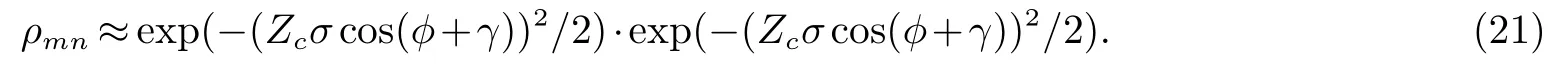
在功率谱为拉氏分布时CA阵列的阵元m和n间SFC为：

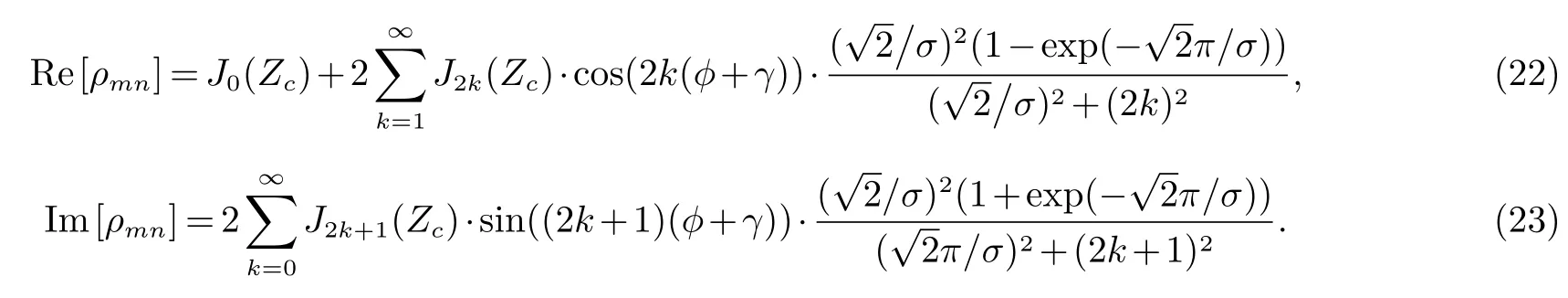
其近似理论式为：

以上根据Massive MIMO在诸多功率谱PAS分布，分别导出LA和CA阵列的阵元m和n间的衰落信号相关性SFC函数的闭合表达式，且讨论了波达信号PAS小角度扩展参数时的近似理论算式.

3 Massive MIMO信道容量

在移动通信系统性能分析中，信道容量决定了无线系统的性能，对于系统设计具有重要的意义.许多文献研究了IID(Independent identical distribution)复高斯信道模型，奠定了MIMO信道容量分析的理论基础，本节利用基于阵列配置Massive MIMO天线的衰落空间信号特性以及功率传输特性，研究分析阵列、近似算法以及空间方位特征对Massive MIMO信道容量的影响[17−21].由于随机Massive MIMO信道的信道容量是随机变量，故通常利用各态历经容量、互补累积分布函数，描述随机MIMO信道容量的统计特性.假设发射端不具有任何的信道信息，则发射功率将均匀分配在每个Massive MIMO发射阵元上，此时一个突发(burst)时间内信道容量的统计均值为[15−19]：

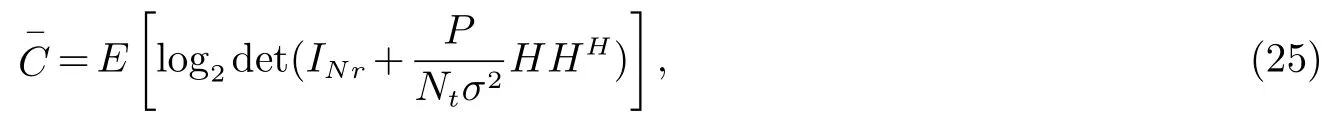
其中，INr是单位矩阵，P/σ2为信噪比SNR，信道矩阵H可以表示为式中Rr是接收端的阵元间相关矩阵，Rt是发射端的阵元间相关矩阵，Hw由詹斯不等式Elogx≤logEx和log2|·|的容量可得：

其中R=E[H•HT]，阵元γij在R矩阵中表示为：

其中∗为复共轭.假设则归一化相关系数γhij可以定义为：

由此可以看出，阵列信号衰落相关信道对Massive MIMO信道容量具有很大的影响，通过理论计算和仿真实验得出在特定条件下近似计算法的拟合度，定量分析了近似计算法的适用性和对Massive MIMO阵列的计算效率，其结果对未来新技术研究和创新具有重要意义.

4 分析结果与讨论

过去很多文献[10-18]研究表明，根据收发终端具体情况小规模MIMO阵列模型通常可设计为MIMO LA，CA或者Y阵列等模型，详细分析可见文献[13-16].其各类MIMO阵列模型均有其优缺点，如CA和Y型对称型阵列，均可提供0到360度全方位和无模糊的二维方位角度信息使得在任何方向上都具有相同的阵列孔径.本文重点分析和讨论基于二维空间Massive MIMO RA和CA模型见图4，在不同波达信号功率谱PAS分布下，阵元信道SFC近似算法及其复杂性，其分析方法也可应用于分析其它Massive MIMO阵列.本文所取研究系统计算和仿真参数，如表1所示.

表1 系统计算与仿真参数

4.1 衰落相关性SFC与近似计算结果

图5(a)、(b)和(c)分别为MIMO线性LA天线阵列在PAS均匀、高斯以及拉氏分布下(小扩展角度)，阵元m与n间（见图4(a)）的SFC精确理论结果和近似结果.由结果可看出，随着天线阵元间距离增大，空间衰落相关性SFC越小并逐渐趋于零.另外，PAS角度扩展越大，空间衰落相关性SFC就越小.其物理意义可以理解为，若天线阵元间距越大或者到达信号的角度分布范围越宽，则MIMO阵元间相互影响效应越小.由图5(a)示当∆≥15˚时，天线阵元间距d越小（紧凑型MIMO阵列），近似分析结果几乎与精确分析重合.但随着d的增大，近似分析结果会出现一定的误差.当∆≤5˚时，对于任意的天线阵元间距，近似分析与精确分析完全拟合.当波达信号功率谱PAS为高斯和拉氏分布时，图5(b)和图5(c)可分别示近似结果在σ≤15˚时与精确结果能较好地拟合.当波达信号PAS扩展角较大和阵元间距较大时，近似结果存在明显误差，但是总体趋势上还是与精确结果较为相符.因此本文近似方法对Massive MIMO性能分析具有极其重要的作用，表2所示可大量节省系统模拟仿真计算时间.

由于算法上采用小角度近似法，其是否适合于大角度情况或者是否有特殊状态性，图5(d)示一些特殊大角度情况的计算仿真结果.当取∆或σ的大角度为45˚时，精确结果与近似具有明显误差.也即在紧凑型阵列分析时，近似算法具有较好适应性.表2示本文近似算法能极大地节省计算机计算时间，提高数值计算效率.由此分析得知，在分析扩展角较小或紧凑型阵列时，MIMO系统的性能仿真均可利用近似算法.在使用主频3.5GHzDELL工作站，由表2可得，两阵元间SFC近似计算比精确计算可节省相当可观时间，显示近似算法具有非常好的计算效率和较高精度.

表2 LA阵列功率谱角能量分布下算法运行时间（单位：秒[s]）

图5 LA阵列阵元间信号衰落相关性SFC精确值与近似值（φ=45˚、∆或σ∈{2˚,5˚,15˚,25˚与d/λ∈{0,5}}）

如图4(b)Massive MIMO CA阵列，图6(a)、(b)和(c)分别是CA阵列在PAS均匀、高斯以及拉氏分布下，阵元m与n间SFC精确和近似结果.随着天线阵圆环半径R增大，空间衰落相关性SFC越小并逐渐趋于零.另外，在功率谱PAS分布角度扩展越大，SFC下降速度越快.可理解为阵圆环半径越大，将导致阵元间距越大或者到达信号的角度分布范围越宽，表示阵元间的相互影响效应越小，使得阵元间的耦合效应越小.图6(a)示，当PAS∆≥15˚，紧凑型MIMO阵列R/λ≤0.5较小时，近似分析曲线几乎与精确曲线重合.但随阵列圆环半径R的增大，近似结果会出现一定的偏差.当∆≤5˚时，对于任意的环半径，近似分析与精确曲线都几乎重合.当功率谱PAS为高斯和拉氏分布时，图6(b)和图5(c)得到近似算法在σ属于15˚和25˚以内都能与精确理论结果有较好拟合.因此，在PAS扩展角和阵列环半径R较大时，近似结果才存在明显较大偏差，但总体趋势还是与理论结果相符.

当∆或σ大角度取45˚时，图6(d)中精确结果与近似具有明显误差.另外，当功率谱PAS扩展角较小时，近似算法，可用于分析紧凑型Massive MIMO阵列系统，且算法能极大节省计算时间和提高计算效率.同样，在使用主频3.5GHzDELL工作站，表3显示出CA环阵列阵元间SFC近似计算比精确计算可节省相当可观时间，算法具有非常好的效率和很高的精度.另外相比LA和CA近似算法，由于CA阵列计算中多使用三角函数使得计算稍复杂，且需要花费更多的CPU时间.由以上分析可知，本文提出的近似算法能较好适用于研究紧凑型MIMO阵列，且算法均能极大地节省计算时间，提高数值计算效率.未来可分析和仿真5G系统所采用的各种大规模Massive MIMO.

图6 CA阵列阵元间信号衰落相关性SFCC精确值与近似值（φ=45˚、ψ=30˚和60˚、∆或σ∈{2˚,5˚,15˚,25˚与R/λ∈{0,5}}）

表3 CA阵列功率谱角能量分布下算法运行时间（单位：秒[s]）

4.2 Massive MIMO信道容量

信道容量是衡量多天线系统MIMO性 能的关键指标，在理想情况下，信道容量随着阵列阵元数的增加而线性增大关系.如前所述，紧凑的天线阵列会使阵元间SFC增加，从而会直接影响Massive MIMO的信道容量.因此在多径衰落信道中，对MIMO系统天线阵列配置时，为了减少阵元间SFC应尽可能地占据足够的空间，并综合考虑整体阵列结构，使得相关性矩阵H诸行列元素均尽可能较小，才能最有效地提高系统的信道容量.本文在此主要考虑由“MIMO”、“准Massive MIMO”以及“Massive MIMO”的LA和CA 3×3、15×15和64×21阵列，定量分析信道容量以及讨论近似算法效率，为未来更多Massive MIMO阵列设计提供了重要的理论和思路.

图7(a)和(b)示MIMO LA阵列在高斯以及拉氏分布下，多天线MIMO系统信道容量.在功率谱PAS扩展参数σ取较大值，其结果趋于功率谱均匀分布情况.由结果可看出，随着SNR和Massive MIMO阵列数增大，系统信道容量由急剧增大到缓慢增长并趋于稳定平滑过程，由此说明在此IID复高斯信道下MIMO信道容量并非SNR和阵元数成线形增长关系.取系统参数SNR=10dB为例，在对比LA 3×3下Massive MIMO 15×15和64×21的阵元数分别增长5倍和149倍，其MIMO信道容量仅增长了5倍和8倍左右.由此可以看到，Massive MIMO阵列并非阵元数越多越好，其紧凑型使得阵元间SFC以及电磁互耦效应会极大地影响其接收性能的提高.阵元数较少表示在相同空间下，阵元间的相互影响效应越小，耦合效应也越小，使得Massive MIMO的性能设计与应用时具有一个最优值.另外，由于集成技术飞速发展可在成本极低情况下，为了不占用更多资源，可增加阵元数来获取一定的信道容量增长，这也是极具商业价值的.对比图7(a)和(b)结果，因为高斯和拉氏分布相似，所以在功率谱PAS高斯和拉氏分布下LA信道容量相差较小.故其功率谱PAS中高斯分布适于室外无线信道环境，拉氏分布更适于室内无线信道，当然不同的信道环境应取相应PAS扩展参数σ值.由前面结果可知，当d/λ较小时，精确理论结果与近似结果具有较好拟合性.也即在紧凑型Massive MIMO阵列分析时近似算法具有很好适应性.由表4示本文提出的近似算法对Massive MIMO信道容量的计算速度.使用主频3.5GHzDELL工作站，对Massive MIMO信道容量的计算会节约可观时间.近似算法具有非常好的计算效率和较高的精度，因此近似算法可能在未来对其它多种Massive MIMO系统分析和仿真具有重要意义.

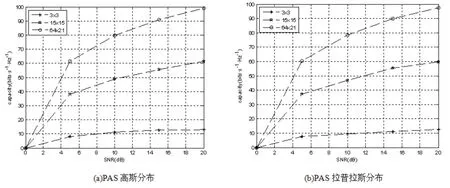
图7 LA阵列阵元间信道容量（d/λ、φ=0˚、σ=45˚）

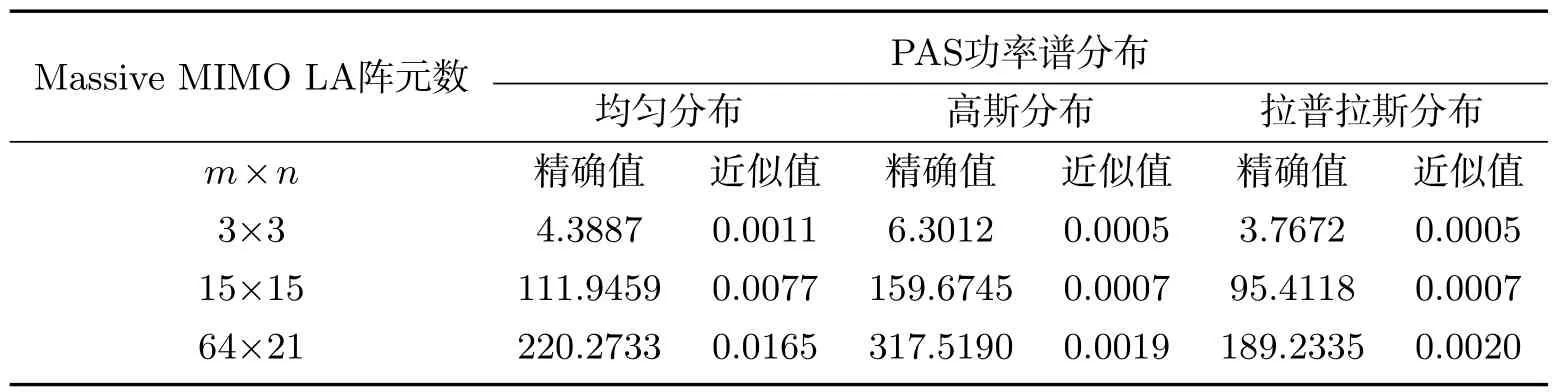
表4 LA阵列不同天线数和功率谱分布下信道容量运行时间（单位：秒[s]）

图8(a)和(b)示MIMO CA阵列在高斯以及拉氏分布下，不同阵元数的Massive MIMO系统信道容量.与MIMO LA阵列相同，随着信噪比SNR增大以及阵元数增大，其信道容量由开始的急剧增大到缓慢增长，并逐渐趋于平稳并呈现非线形增长关系.在SNR=10 dB时，如果MIMO CA阵元数分别增长5倍和149倍，其信道容量增长与LA阵列相比稍好，此种情况在拉氏分布时表现更加明显.说明在同样阵列空间下，CA阵列信道容量优于LA阵列，且在提高MIMO性能时阵列结构设计具有一定的潜力.表5示近似算法对Massive MIMO CA阵列信道容量的计算速度.使用主频3.5GHzDELL工作站运算结果显示，信道容量的计算同样会节约可观时间.近似算法具有非常好的计算效率和较高的精度.相比表4和5结果，CA阵列近似计算时间明显高于LA阵列耗费时间，原因是CA阵元矢量式大量使用三角函数表达关系.本文对Massive MIMO信号衰落相关性SFC以及对MIMO信道容量进行了探讨.在考虑拟合室内外环境的功率谱PAS下，提出SFC近似算法并定量分析了近似算法的适用性和计算时间效率，为此提供了分析MIMO信道重要的理论和设计.因此本文研究可在以下几方面指导Massive MIMO研究和探讨：

(1)Massive MIMO阵列性能与阵元数并非成正比关系，其空间结构形态与紧凑型可能使得阵元SFC以及互耦增大将影响性能的提高，使得Massive MIMO设计时存在最优设计.本文近似算法提供理论分析和优化方法，空间结构设计中可考虑优化设计，激发MIMO丰富的传播多径，使之充分有效利用空间资源.(2)设计中需要充分利用天线分集技术，保持波达信号的独立性而降低MIMO阵元自身的空间因素.由SFC结果可知其衰落具有周期性特征，在设计中，应据分析结果，尽量选取阵元间具有低相关性节点，增大极化隔离与端口隔离.(3)由过去研究得知，功率谱PAS高斯分布适于拟合室外信道环境，拉氏分布适于室内信道.因此可针对不同的信道环境，选取PAS扩展参数值可精确拟合各种信道试验、各种Massive MIMO.本文所提出的近似算法，证明其结果与精确计算具有较好拟合性和适应性.对Massive MIMO阵列设计分析可采用如图3所示的多维度阵列布局，以获得高密度的天线布局与性能.

图8 CA阵列阵元间信道容量（R/λ、φ=0˚、σ=45˚）

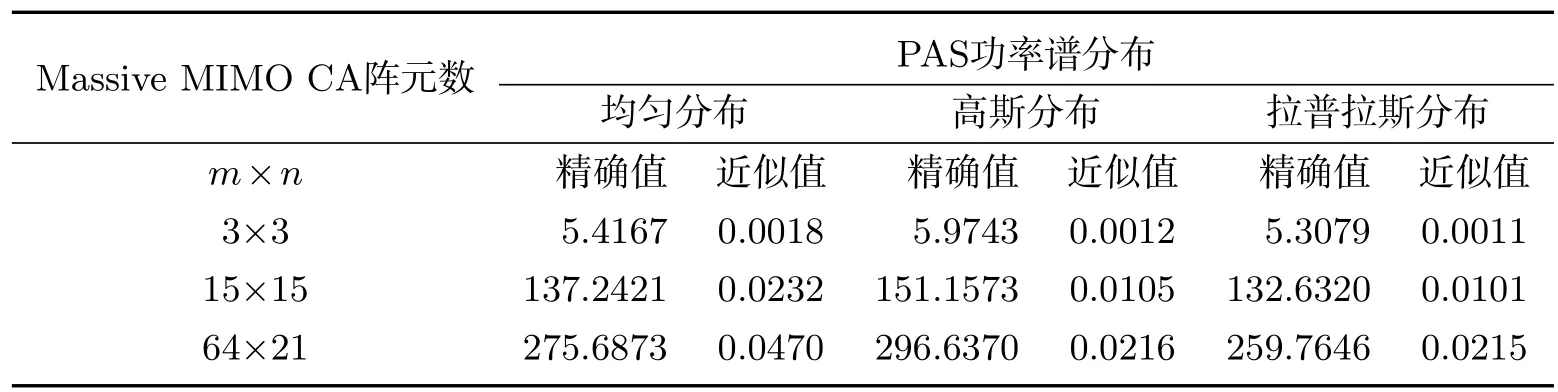
表5 CA阵列不同天线数和功率谱分布下信道容量运行时间（单位：秒[s]）

5 结论

针对Massive MIMO技术，本文重点研究其空间衰落信道模型及其近似算法.分析了MIMO信道特阵、阵列间距、波达信号到达角和功率谱扩展对MIMO天线系统信道的影响，取得了系统性能和近似算法效能.导出了在典型PAS下的SFC函数的闭合表达式，推导在各种角度扩展时的近似算法式和探讨了其计算效能，建立起Massive MIMO基本模型.结果揭示了其信道特征的诸多关键因素，阐明阵元接收信号强度、阵元衰落信号SFC和信道矩阵分布特征关系.由此通过理论计算和仿真实验得出近似算法在特定条件下具有很好的拟合度，定量分析了近似算法在对系统分析时的适用性和计算效率.结果证明近似算法能极大地减低理论计算复杂性，提高分析大规模多天线系统的能力.