基于改进频繁模式树的最大频繁项目集更新挖掘算法

赵群礼，郭玉堂，史君华

基于改进频繁模式树的最大频繁项目集更新挖掘算法

*赵群礼，郭玉堂，史君华

（合肥师范学院计算机学院，安徽，合肥 230061）

在挖掘最大频繁项目集的过程中，通过改变最小支持度阈值可以挖掘更有用的最大频繁项目集，为此提出了一种最大频繁项目集更新挖掘算法UAMMFI(Updating Algorithm for Mining Maximal Frequent Itemsets)。算法基于改进后的频繁模式树结构，在更新挖掘过程中，不需产生候选项目集和条件模式树，并且充分利用先前已挖掘的最大频繁项目集中包含的信息，快速更新挖掘出最小支持度阈值变化后的最大频繁项目集。实验结果表明，算法能够高效更新挖掘最大频繁项目集。

关联规则；最大频繁项目集；改进频繁模式树；最小支持度阈值

0 引言

在关联规则挖掘的概念提出以后，业界对关联规则挖掘算法进行了大量的研究，其中挖掘最大频繁项目集的算法是一个重要的研究方向。由于最大频繁项目集的子集都是频繁项目集，将挖掘频繁项目集的任务转化为挖掘最大频繁项目集，可以减少挖掘过程中的计算量，提高挖掘的效率。业界已提出的较为著名的最大频繁项目集挖掘算法有GenMax[1]、SmartMiner[2]、DMFIA[3]、FpMax[4]、Mafia[5]等。在这些算法提出以后，研究人员又在上述算法的基础上进行了改进，提出了一些新的算法，如：Hybrid GeneticMax[6]、FPMax-reduce[7]、IFPmax[8]、Max-IFP[9]、MFPAS[10]等。这些算法在固定的最小支持度阈值（表示为）和数据库（表示为TDB）中能有效挖掘最大频繁项目集。但在实际应用中，为了发现更有用的最大频繁项目集，用户要频繁地调整，而TDB也会随着时间发生变化，对于和TDB变化以后，如何高效更新挖掘最大频繁项目集是一值得研究的课题。一种简单的解决方案是在和TDB变化以后，调用最大频繁项目集挖掘算法再重新计算一遍，找出变化后的最大频繁项目集，但这种方法的不足之处是先前的挖掘结果和计算量都被浪费，而且对于海量数据来说，重新挖掘需要花费大量的计算，因此需要研究专门的算法用于最大频繁项目集的更新挖掘。在文献[3]中首先提出了一种在TDB变化时的更新挖掘最大频繁项目集算法UMFIA，此后的很多研究也是针对TDB变化时的更新挖掘，而针对变化后更新挖掘最大频繁项目集的研究很少。为此，本文提出了一种基于改进频繁模式树的最大频繁项目集更新挖掘算法UAMMFI(Updating Algorithm for Mining Maximal Frequent Itemsets)，能够在变化以后高效更新挖掘最大频繁项目集。

1 相关问题

1.1 相关定义

其中N表示TDB中包含的记录数，|TDB|表示数据库中的记录总数。在TDB中的支持数()与支持度()的关系为：() =()×|TDB|。

定义1：若项目集的支持度()≥，则称t为频繁项目集。

定义2：对于项目集，若()≥，而任意项目集⊃，都有()<，则称为最大频繁项目集，表示为MFI(Maximum Frequent Itemsets)，所有最大频繁项目集的集合表示为MFS(Maximum Frequent Sets)。

1.2 频繁模式树

频繁模式树结构是由Han等人在文献[11]中提出的，基于频繁模式树结构挖掘TDB中的频繁项目集，在挖掘过程中不用产生候选项目集。在频繁模式树结构中，每个树节点包括四个数据项：node-name(存储节点的项目名)、node-count(存储到达此节点的子路径所对应的事务数)、node-link(指向树中同名节点)和node-parent(指向父节点)。为便于遍历，建立一个头表head-table，其中包含三个数据项：item-name、item-count和head-link，item-name表示频繁项目名，item-count表示项目的支持数，head-link是指向同名节点链的头指针。建立频繁模式树的算法在文献[11]中有详细描述，本文不再赘述。图1是根据表1中的数据库在最小支持数等于3时构建的频繁模式树。

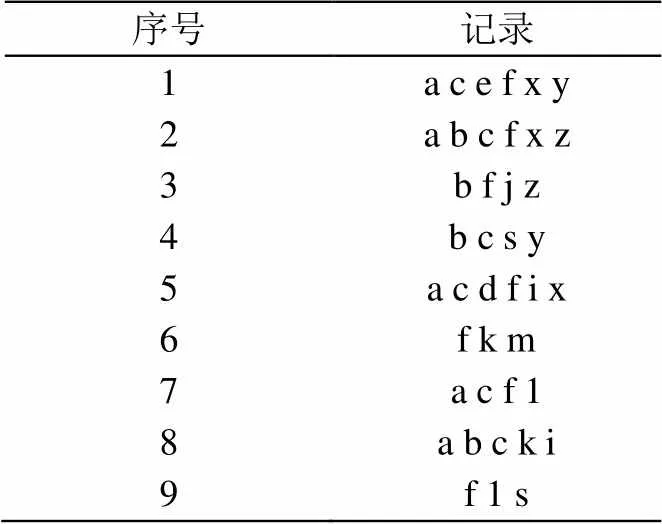
表1　事务数据库TDB

图1　根据表1数据库建立的频繁模式树

1.3 改进频繁模式树

基于频繁模式树结构虽然可以有效挖掘频繁项目集，但该结构不适合直接用于更新挖掘最大频繁项目集，需要对其进行改进。根据频繁模式树的构造过程，当一个节点的计数大于等于最小支持数时，以该节点为后缀的路径对应的项目集必然是频繁项目集，也有可能是最大频繁项目集，如果能知道某个频繁项目集不是最大频繁项目集，则其子集都可以不用再遍历，这样可以有效减少树中遍历的节点数。为此，在每个节点中增加一个域，用于表示树中以某节点为后缀的路径对应的项集是否是最大频繁项目集，0表示不是最大频繁项目集，1表示可能是最大频繁项目集。由于每个节点路径对应的项目集都有可能是最大频繁项目集，所以每个节点的域都初始化为1。另外，在头表中增加一个域，用于标记对应项目是否已遍历，1表示已遍历，0表示没有遍历，并根据文献[12]提出的方法，减少挖掘最大频繁项目集过程中对超集的检测。在构造频繁模式树时，树中同层的节点按照头表中的顺序从左至右排列。图2给出了根据表1建立的改进后的频繁模式树，最小支持数为3。在后面各部分所提到的频繁模式树，都指的是改进后的频繁模式树。

图2　改进后的频繁模式树

根据改进后的频繁模式树，可以得出以下性质：

性质1：设m和m是head-table中的两个频繁项目，且m在m的下方，则以m为后缀的项目集I一定不会是以m后缀的项目集I的子集，并且可能存在II。

证明：根据改进后的频繁模式树的结构，频繁项目在head-table中是按照支持数降序排列的，若m和m出现在同一条路径中，则m必然在m的后缀路径中，性质1成立。

性质2：在改进频繁模式树中的任意一个节点链上的两个节点1和2，若1在2的左侧，且1和2有共同的祖先节点（null根节点除外），则以1为后缀的项目集I1一定不是以2为后缀的项目集I2的子集。

证明：根据树的构造过程可知，项目集I1和I2不完全相同，而且1所在的层数一定不小于2所在的层数，因此|I1|≥|I2|，即I1一定不是I2的子集，性质2成立。

2 最大频繁项目集更新挖掘算法UAMMFI

设TDB保持不变，只有最小支持度发生变化。设变化前的最小支持度表示为，变化后的最小支持度表示为′，对应的最大频繁项目集的集合分别表示为MFS和MFS′，频繁项目集合表示为和′。

性质3：设事务数据库TDB不变，若′ <，则′；若′ >，则′。

性质4：设TDB不变，当′ <时，对MFS中任意一个最大频繁项目集，则′′，使得′；同理，当′ >时, 对于′′，则，使得′。（证略）

性质5：设和分别是对应于和′的改进后的频繁模式树，当′ <时，有″=′-，则″中的项目一定为′的叶节点或叶节点的前缀节点，且在中的项目之后；当′ >时，有″=-′，则″中项目在′中无对应的节点。

证明：当′ <时，中项目的支持度小于中所有项目的支持度，根据频繁模式树的构造过程可知，中的项目必然排在中的项目之后，在′中作为中项目的后缀，所以中的项目或者为叶子节点，或者为″中其他项目的前缀；当′ >时，因″中的项目均为′下的非频繁项目，所以在′中没有″中项目对应的节点，性质5成立。

性质6：对于频繁模式树中某节点N，若存在N. node-count ≥ minsup×|TDB|，则以N为后的路径{1,2,…,p}对应的项目集I={I1,I2,…,I}必为频繁项目集。

证明：根据频繁模式树的构造过程可知，树中的节点是按照支持数降序排列的，如果节点的计数大于等于最小支持数，则其前缀中的所有节点的计数也必然大于等于最小支持数，因此以该节点为后缀的路径对应的项目集必为频繁项目集，性质6成立。

由于最小支持度发生变化分为′ >和′ <两种情况，在这两种情况中，都需要对原有的频繁模式树进行调整，以用于挖掘MFS′，下面分别进行阐述：

（2）当′ <时，根据性质4，MFS中的项目集一定是′中项目集的子集，根据性质3，在下的非频繁项目可能变成下的频繁项目，因此需要扫描数据库TDB将新增的下的频繁项目找出来，并调整原频繁模式树，方法如下：（1）扫描一次TDB，找出新增的频繁项目″，并按照降序插入到原有的head-table中，并将置为0；（2）再次扫描TDB，将每个记录中新增的频繁项目按照头表中的顺序从左至右依次插入到频繁模式树中，根据性质5，新增的频繁项目可能是树中的叶子节点，也可能是其他新增项目的前缀节点。

通过以上分析，给出UAMMFI算法描述如下：

输入：′、、MFS、改进的频繁模式树。

输出：MFS。

（1）MFS′={ }；

（2）(minsup′ >){

（3）将的头表中不满足′的项目的visited设为1;

（5）(sup()≥′) {

（6）MFS′=MFS′∪;

（7）搜索项目[]的节点链中的节点，若是的子集，则将对节点的都设为0，如果节点链中所有节点的都为0，则将项目[]的标记设为1; }

（8） }

（9） 调用UAMMFI(T);

（10）}

（11）(′<) {

（12）扫描TDB，找出满足的新增项目，并按支持度降序放入的head-table中;

（13）再次扫描TDB，将每个记录中新增项目对应的路径添加到中;

（14）调用UAMMFI(T);

（15）}

Procedure UAMMFI( Tree ){

（1）(=;>0;--){ //k等于Tree中head-table的长度

（2）(head-table[i].visited≠1) then { //遍历树中未访问项目的节点链

（3）-[].=1;

（4）=-[].-;

（5）(p≠) do {

（6）(p.= 0) { p =-; }

（7）(.-≥′) { //是最大频繁项目集

（8）搜索节点链中右侧的其他节点，如果等于1，并且以为后缀的项集是以为后缀的项集的子集，则将设为0；

（9）p. node-parent.flag = 0;

（10）MFS′=MFS′∪Ip;

（11）p = p.node-link; }

（12）else{ //不是频繁项目集

（13）搜索节点链中右侧的其他节点，如果等于1，并且以为后缀的项集I是以为后缀的项集I的子集，则=+;}

（14）}//end while

（15）}//end if

（16）}//end for

（17）}//end Procedure

3 算法实验对比和性能分析

3.1 实验对比

在实验中，用C++语言在酷睿i7、2GHZ处理器、8GB内存、Windows 10系统的计算机上实现了UAMMFI算法和FPMax算法，并采用了与文献[7]相同的mushroom测试数据库。实验方案为：我们先设定最小支持度为0.3，并用Fpmax算法挖掘出此时的MFS，然后用UAMMFI算法在最小支持度依次变化为0.2、0.1、0.05、0.02、0.01时分别进行更新挖掘，得到对应的MFS′，最后最小支持度再按照0.02、0.05、0.1、0.2、0.3依次变化，再用UAMMFI算法依次进行更新挖掘。为了对比，我们用Fpmax算法分别在0.2、0.1、0.05、0.02、0.01时重新挖掘一遍，表2和表3给出了实验结果数据，图3和图4给出了实验结果对比图。从实验结果可以看出，UAMMFI算法在进行最大频繁项目集更新挖掘时的效率要好于Fpmax算法，而且算法的性能稳定，在不同的支持度阈值下，算法执行时间的变化幅度不大，也说明算法具有较好的执行性能。

表2　最小支持度由大变小的实验数据

表3　最小支持度由小变大的实验数据

图3 最小支持度阈值由大变小

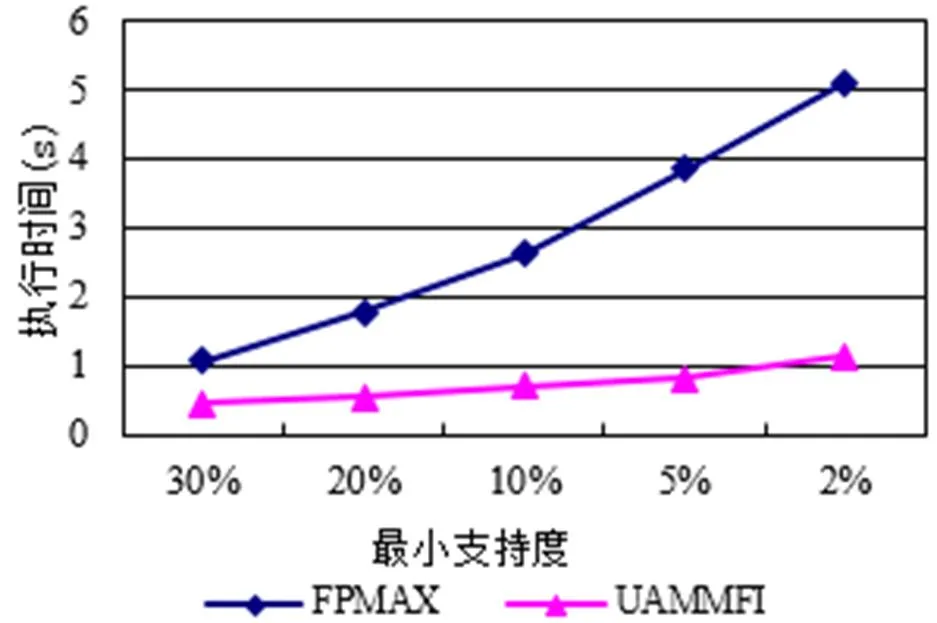
图4 最小支持度阈值由小变大

3.2 性能分析

UAMMFI算法充分利用改进后的频繁模式树的特点和先前已挖掘的中包含的信息，在挖掘过程中不产生候选项目集和条件模式树。算法所需的存储空间仅为存储频繁模式树的容量，计算过程中不需要占用额外的存储空间，算法所需的计算时间主要消耗在自底向上自左至右搜索最大频繁项目集上，根据改进后的频繁模式树，在最好情况下，算法的性能可以达到()（为头表的长度），在最坏情况下算法性能要达到()（为头表的长度，为最长节点链的长度），而且由于在树中的每个节点中设置有标记，对于不可能成为最大频繁项目集的节点路径，不需再进行搜索，因此有效减少了搜索过程中的计算量。

另外，当′<时，虽然需要扫描数据库，将满足′的新项目添加到改进后的频繁模式树中，由于不需要重新建立频繁模式树，仅需将新项目按顺序插入到树中现有路径的后面，所以所需的计算量要比新建频繁模式树所需的计算量小很多。当′ >时，由于′中项集是中项集的子集，因此不需要再扫描数据库，仅需在原有频繁模式树中即可挖掘出满足′的最大频繁项目集，由于树中不满足′的节点不会再被遍历，所以挖掘所花费的计算量要比′<时所需的计算量小，实验结果也证明了这一点。

4 结束语

在最小支持度阈值变化时更新挖掘最大频繁项目集，不需要在数据库中重新挖掘一遍，因此可以减少挖掘过程中的计算量。本文提出的最大频繁项目集更新挖掘算法UAMMFI，基于改进后的频繁模式树结构，挖掘过程中不会递归构建条件模式树，并通过树中节点设置标记，减少了遍历节点的数量，节约了计算时间，从而提高了算法的效率。根据实验对比结果和性能分析可以看出，该算法可以有效解决在最小支持度阈值发生变化时更新挖掘最大频繁项目集的问题。

[1] Gouda K, Zaki M J. Efficiently Mining Maximal Frequent Itemsets[C]. IEEE International Conference on Data Mining. IEEE, 2002:2405-2409.

[2] Zou Q, Chu W W, Lu B. SmartMiner: A Depth First Algorithm Guided by Tail Information for Mining Maximal Frequent Itemsets[C]. Proceeding of the IEEE International Conference on Data Mining, 2002:570-577.

[3] 宋余庆,朱玉全,孙志挥,等. 基于FP-Tree的最大频繁项目集挖掘及更新算法[J].软件学报,2003.14(9): 1586-1592.

[4] Grahne G, Zhu J F. High performance mining of maximal frequent itemsets[C].Proceeding of the 6th SIAM International Workshop on High Performance Data Mining,2003:135-143.

[5] Burdick D, Calimlim M, Flannick J, et al. MAFIA: a maximal frequent itemset algorithm[J]. IEEE Transactions on Knowledge & Data Engineering, 2005, 17(11):1490-1504.

[6] Kabir M M J, Xu S, Kang B H, et al. A Hybrid GeneticMax Algorithm for Improving the Traditional Genetic Based Approach for Mining Maximal Frequent Item Sets[J]. International Journal of Computer Science & Network Security, 2014, 14(10):27-35.

[7] Niu X Z, She K. Mining Maximal Frequent Item Sets with Improved Algorithm of FPMAX[J]. Computer Science, 2013, 40(12):223-228.

[8] Ning H, Wang S, Cui L, et al. An algorithm for mining maximal frequent patterns based on improved FP-tree[J]. Applied Science & Technology, 2016,43(2):37-43.

[9] Pan Z, Liu P, Yi J. An Improved FP-Tree Algorithm for Mining Maximal Frequent Patterns[C].International Conference on Measuring Technology and Mechatronics Automation. IEEE Computer Society, 2018:309-312.

[10] Karim M R, Cochez M, Beyan O D, et al. Mining maximal frequent patterns in transactional databases and dynamic data streams: A spark-based approach[J]. Information Sciences, 2018, 432:278-300.

[11] Han J, Jian P, Yiwen Y. Mining frequent patterns without candidate generation[C]. Proceeding of the 2000 ACM SIGMOD International Conference Management of Data,Dallas,2000:1-12.

[12] 李少华,吕志旺,车德勇,等. 基于有序FP-tree的最大频繁项集挖掘算法[J].东北师大学报:自然科学版,2016, 48(2):65-69.

AN UPDATING ALGORITHM FOR MINING MAXIMAL FREQUENT ITEM SETS BASED ON IMPROVED FREQUENT PATTERN TREE

*ZHAO Qun-Li, GUO Yu-Tang, SHI Jun-Hua

(The Department of Computer Science and Technology, Hefei Normal University, Hefei,Anhui 230061, China)

In mining the maximal frequent item sets, we can get more useful maximal frequent item sets by changing the minimum support threshold. Furthermore, we proposed a new algorithm UAMMFI(updating algorithm for mining maximal frequent item sets) for mining maximal frequent item sets for the demand. The algorithm didn't generate candidate item sets and construct conditional pattern tree based on improved frequent tree. We also make full use of the information contained in maximal frequent item sets previously mined in the process of updating mining maximal frequent item sets. Finally, we can efficient mining new maximal frequent item sets after the minimum support threshold change. Based on experiment results, we can see that the algorithm has excellent performance.

association rules; maximal frequent item sets; improved frequent pattern tree; minimum support threshold

1674-8085(2018)04-0043-05

TP311

A

10.3969/j.issn.1674-8085.2018.04.008

2018-03-11；

2018-05-17

国家自然科学基金(61503116)；安徽省高校自然科学研究重点项目(KJ2016A585)

*赵群礼(1974-)，男，安徽霍邱人，讲师，硕士，主要从事模式识别和数据挖掘研究(E-mail:zql@hfnu.edu.cn);

郭玉堂(1962-)，男，安徽安庆人，教授，博士，主要从事图像识别和数据挖掘研究(E-mail:guoyutang@hfnu.edu.cn);

史君华(1981-)，女，安徽合肥人，副教授，硕士，主要从事模式识别与数据挖掘方面的研究(E-mail:junhuash@163.com).