抵御执行器故障扰动的二次性能指标可靠控制
张 瑶,姚 波,王福忠
抵御执行器故障扰动的二次性能指标可靠控制
*张 瑶1,姚波1,王福忠2
(1.沈阳师范大学数学与系统科学学院,辽宁,沈阳 110034;2.沈阳工程学院基础教学部,辽宁,沈阳 110136)
针对线性不确定系统,在设计不确定系统保性能问题的基础上,提出了带有执行器故障的二次性能指标可靠控制问题。第一,设计静态输出反馈控制器给出了系统渐近稳定的充分条件,且满足二次性能指标。第二,考虑执行器连续增益故障,此时系统在原静态输出反馈控制器下无法维持原性能甚至是稳定性。第三,利用LMI给出了静态输出反馈可靠控制器且满足二次性能指标的设计方法。此控制器可使线性不确定系统在发生执行器故障后满足二次性能指标且依然保持稳定。最后,根据MATLAB仿真结果证明了该可靠控制器的科学性和严谨性。
静态输出反馈;执行器故障;二次性能指标;线性矩阵不等式(LMI);保性能
保性能控制是指系统在其允许扰动的范围内保证系统渐近稳定且二次性能指标有界。在保性能控制进行大量研究以来,不确定系统的保性能控制受到了人们的高度关注。文献[1-4]描述了不确定系统下的保性能控制的相关研究,提出了保性能控制器的设计方法。然而,在实际的控制系统中,系统不会永远在所期望的理想状态下运行,很大程度上会出现故障且无法避免,一些故障一旦发生,会使系统失去其优质的性能甚至失去稳定性。所以,针对故障设计相应的控制器,使系统依然能保持原有的性能且稳定是至关重要的。文献[5-8]为学者对可靠控制的相关研究,在系统出现故障的情况下,系统依然能够渐近稳定。保性能问题与可靠控制问题的结合是可以在满足二次性能指标的同时即使系统出现故障,系统依然能保持稳定的关键,是具有实际研究价值的。所以,保性能可靠控制的研究进入了人们的研究领域当中。文献[9-13]给出了二次性能指标问题的一些研究思路及保性能可靠控制的一些设计方法。
本文考虑线性不确定系统,引入了静态输出反馈控制器,避免了状态反馈在实际系统中难以采集状态的问题,动态输出反馈的过程又过于复杂。给出了基于二次性能指标的静态输出反馈控制器的设计算法。在此基础上,考虑执行器故障,提出了带有执行器故障扰动的保性能可靠控制,给出了基于二次性能指标的静态输出反馈保性能可靠控制器的设计算法,使得系统即使发生故障,其依然能保持渐近稳定且满足二次性能指标。最后,通过仿真算例证明出本文结论的正确性和科学性。
1 问题描述
首先考虑如下线性不确定系统:

△()
式中,为适维维数的常数矩阵;()为未知的时变实值连续矩阵函数,其元素Lebegue可测,且:
θ()() ≤
对线性系统(1)引入静态输出反馈控制器
()=() (2)
由此得到闭环系统

执行器连续增益故障矩阵模型描述为:

下面考虑执行器故障(4),此时系统可以表述为:
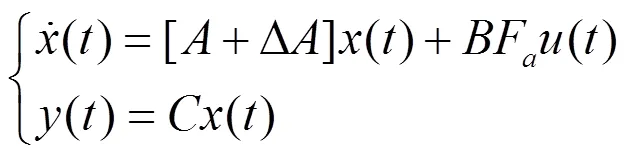
由此得到新的闭环系统

其中,K为可靠控制器增益矩阵其为待设计矩阵。
对线性系统(1)及(5)定义二次性能指标

为系统(1)及(5)的性能函数,式中=Q>0为给定的加权矩阵。
引理1对于线性连续系统和性能函数,如果存在正定矩阵,使得+AP<-,则系统是渐近稳定的,并且性能函数满足:

其中0为系统的初值,即0=(0)。
证明设′=0∴′′=0整理得(′) ′(′)=0。∴是×正定的对称矩阵,且′=0,即′=0。又∵′是可逆的,所以只有=0这个零解。
综上所述,方程只有零解,即′是可逆的,引理得以证明。

2 主要结果
2.1 基于二次性能指标的线性不确定系统静态输出反馈控制器设计
定理1 对系统(1)和性能函数(7)存在静态输出反馈保性能控制器的充分条件是存在标量>0,矩阵和正定的矩阵,使得:

如果LMI的可行解为(,,),则()=-1()为系统(1)的一个静态输出反馈保性能控制器,其中可以由求得。相应的系统性能指标的上界是:
≤Trace(-1)=*
证明由引理1可知,定义二次性能指标

对于系统(1)存在静态输出反馈控制器使得闭环系统(3)是渐近稳定的充分条件是:
1.1 一般资料 选择2015年6月~2017年5月在我院骨科就诊的股骨中下段术后患者48例。纳入标准:临床诊断股骨中下段骨折,行切开复位髓内钉/单钢板内固定术;年龄18~55岁。排除标准:伴有膝关节内骨折、韧带损伤、周围神经损伤,或合并全身多发性骨折等,合并严重心、脑、肺、肝、肾疾病;既往患有膝关节骨关节病史等陈旧性损伤患者;骨肿瘤或肿瘤转移等原因导致的病理性骨折患者。所有患者均签署《康复知情同意书》,48例患者采用随机区组法分为观察组和对照组各24例。2组患者一般资料比较差异无统计学意义,具有可比性。见表1。
+(+△+)+(+△+)P<0 (9)
因为>0是正定矩阵,-1也是一个正定矩阵,取=-1。在式(9)两端同时乘有:
+(+△+)+(+△+)<0 (10)
将△=(),=,=代入(10)中有
++++XA+()+
()+(())<0
设1=+++XA+()+
()+()+(())
其中:π=+++XA+(),=()+
(()),即1=π+φ。
由引理4可知,对任意常数>0,都有
()+(())≤-1()()
所以有
π+-1()() <0
由Schur引理可知:

下证可逆。对等式=两边乘以C得:
VCC=CXC则V=CXC(CC)-1
因为CXC是可逆的,所以V可逆。即定理得证。
2.2 基于二次性能指标的线性不确定系统执行器故障静态输出反馈控制器设计
定理2对系统(5)和性能函数(7),存在考虑执行器故障静态输出反馈保性能控制器的充分条件是存在标量>0,矩阵和正定的矩阵,使得:

如果LMI的可行解为(,,),则()=-1()为系统(5)的一个静态输出反馈保性能控制器,其中可以由求得。相应的系统性能指标的上界是:≤Trace(-1)=*。
证明由引理1可知,定义二次性能指标

对于闭环系统(6)是渐近稳定的充分条件是:
+(+△+BFKC)+(+△+ BFKC)P<0 (12)
因为>0是正定矩阵,-1也是一个正定矩阵,取=-1。在式(12)两端同时乘有:
+(+△+ BFKC) +(+△+ BFKC)<0 (13)
将△=(),=,=代入(13)中有
++ BFKC+XA+
( BFKC)+()+(())<0
设
2=+++ BFKC+XA+( BFKC)+
()+()+(()),
其中π=+++ BFKC+XA+( BFKC),
=()+(()),即2=π+φ。
由引理4可知,对任意常数>0,都有
()+(())≤-1()()
所以有π+-1()() <0。
由Schur引理可知:

下证可逆。对等式两边乘以C得:
VCC=CXC
则V=CXC(CC)-1。因为CXC是可逆的,所以可逆。即定理得证。
3 仿真结果
考虑如下线性不确定系统:


则基于二次性能指标的线性不确定系统静态输出反馈控制器为:
性能指标的最小上界为:*=0.0017,系统渐近稳定,如图1所示。图1表述的是正常的不确定线性系统在无故障的情况下,通过设计基于二次性能指标的静态输出反馈保性能控制器使系统保持渐近稳定。

图1 静态输出反馈保性能控制器使系统渐近稳定
如下为当执行器故障发生时,选择执行器故障增益变化范围满足0.8 ≤1≤ 4.2,2= 1,原始的控制器无法保持系统渐近稳定,如图2。
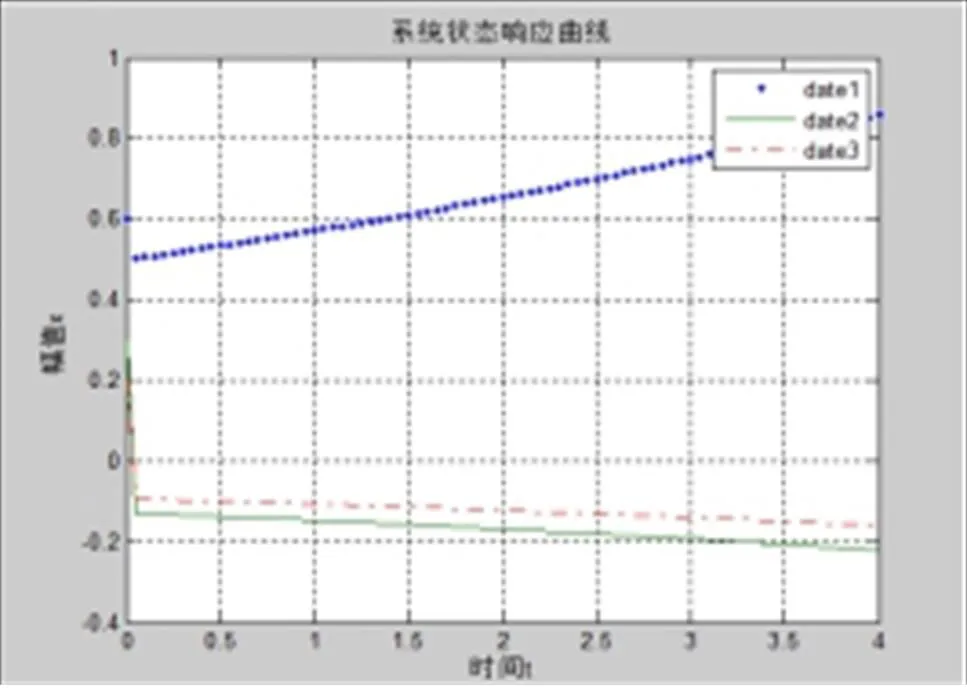
图2 系统出现故障,原控制器无法使系统保持渐近稳定
对于同一故障,使系统保持渐近稳定设计新的带有二次性能指标的静态输出反馈控制器为:

性能指标的最小上界为:*=0.0017,系统再次保持渐近稳定,如图3所示。图3表述的是选择执行器故障的增益变化范围仍是:0.8 ≤1≤ 4.2,2= 1的前提下,重新设计的带有二次性能指标的静态输出反馈控制器,使系统重新保持渐近稳定。
图3 当执行器发生故障时可靠控制器
Fig.3 Reliable controller when the actuator fails
4 结论
本文设计了不确定系统静态输出反馈保性能控制器,在此基础上考虑了执行器故障,可以发现,当系统发生故障时,系统已经失去了稳定性,为了加深一步研究,笔者考虑令保性能控制与可靠控制结合,给出了静态输出反馈保性能可靠控制器的设计算法,即在执行器发生同一故障的情况下,应用该保性能可靠控制器使系统依然保持渐近稳定,同时满足相应的性能指标。最后,通过数值仿真验证了本文定理结论的正确性。
[1] 滕青芳,范多旺. 传感器失效不确定时滞系统指数稳定可靠控制[J].计算机工程与应用,2008(28):223-225-245.
[2] 王申. 基于T-S模型的网络控制系统保性能控制器设计[D].哈尔滨:哈尔滨理工大学,2015.
[3] 王佑恩,肖民卿. 参数不确定δ算子时滞系统的可靠保性能控制[J].福建师范大学学报:自然科学版,2011, 27(5):23-28.
[4] 孙凤琪. 时变时滞不确定奇异摄动系统的保性能控制[J].吉林大学学报:信息科学版,2015,33(6): 637-643.
[5] Veillette R J, Medanic J V, Perkins W R. Design of reliable control system[J].IEEE Transaction on Automatic Control,1992,37(3):770-784.
[6] 王福忠,姚波,张嗣瀛. 具有执行器故障的保成本可靠控制[J].东北大学学报,2003,24(7):616-619.
[7] Zhang P, Cao J, Wang G. Mode-independent guaranteed cost control of singular Markovian delay jump systems with switching probability rate design[J]. International Journal of Innovative Computing Information & Control Ijicic, 2014, 10(4):1291-1303.
[8] Liang Y W, Ting L W, Lin L G. Study of Reliable Control Via an Integral-Type Sliding Mode Control Scheme[J]. IEEE Transactions on Industrial Electronics, 2012, 59(8):3062-3068.
[9] 易宇琴,吴杰康,吴帆. 二次型性能指标优化的多机电力系统负荷频率控制[J].电力学报,2014,29(4):271-277.
[10] 夏超英,张聪. 基于二次型性能指标的混合动力汽车实时优化控制[J].控制理论与应用,2014,31(5):601-606.
[11] 邵克勇,蒋锐,李文成,等.基于二次型性能指标的不确定混沌系统最优控制器设计[J].化工自动化及仪表,2013,40(11):1347-1350,1413.
[12] 王佑恩,肖民卿. 参数不确定δ算子时滞系统的可靠保性能控制[J].福建师范大学学报:自然科学版,2011, 27(5):23-28.
[13] 朱灵波,戴冠中,康军. 具有传感器故障的网络控制系统保性能可靠控制[J].控制与决策,2009,24(7): 1050-1054,1058.
[14] 徐艺超,姚波,王福忠. 梯形区域极点配置静态输出反馈可靠控制[J]. 井冈山大学学报:自然科学版, 2016,37(5):11-17.
QUADRATIC PERFORMANCE CRITERION RELIABLE CONTROL AGAINST ACTUATOR FAILURE
*ZHANG Yao1, YAO Bo1, WANG Fu-zhong2
(1. College of Mathematics and System Science, Shenyang Normal University, Shenyang, Liaoning 110034, China; 2. Department of Preparatory Courses, Shenyang Institute of Engineering, Shenyang, Liaoning 110136, China)
Considering the linear uncertainty systems based on the design of protection performance problem for uncertain systems, the problem of quadratic performance criterion reliable controlwith actuator failures is studied. Firstly, the static output feedback controller was designed, and sufficient conditions for the asymptotically stable of the system was given, at the same time, the quadratic performance criterionis satisfied. Secondly, once the actuator fails, the system can’t remain the original performance or even stable under the action of the original static output feedback controller. Thirdly, a static output feedback reliable controller was designed by LMI, and it satisfies quadratic performance criterion. This controller can make linear uncertain systems keep asymptotically stable after the actuator failure, simultaneously, satisfying the quadratic performance criterion. Finally, the MATLAB simulation is presented to verify the scientific and rigorous of the reliable controller.
static output feedback; actuator failure; quadratic performance criterion; linear matrix inequality(LMI); protection performance
1674-8085(2018)04-0001-05
TP13
A
10.3969/j.issn.1674-8085.2018.04.001
2018-04-16;
2018-05-14
辽宁省科学技术基金项目(20170540823)
*张 瑶(1993-),女,辽宁阜新人,硕士生,主要从事运筹学与控制论研究(Email:821841264@qq.com);
姚 波(1963-),女,辽宁沈阳人,教授,博士,硕士生导师,主要从事可靠控制理论研究(Email:920996024@qq.com);
王福忠(1963-),男,辽宁沈阳人,教授,博士,硕士生导师,主要从事可靠控制理论研究(Email:1228109136@qq.com).

