一种基于调制波电压基波幅值过调制控制方法

李昱兵,陈 跃

(四川虹美智能科技有限公司,绵阳 621000)

0 引 言

变频技术广泛应用于高铁、纺织机械、自动扶梯、数控车床、高速冲床、印刷机械仪以及以空调、冰箱为代表的家用电器领域，诸如对制冷压缩机、室内外风机的控制大量采用变频技术，其具有调节范围宽、节能等特点，同时能够大幅度地提高用户体验和产品舒适度。目前广泛使用的是180°直流变频控制技术， 180°磁场定向控制一般采用空间矢量脉宽调制(以下简称SVPWM)方法进行变频控制，此类方法能够更有效抑制谐波。

传统的SVPWM控制方法，其控制系统框图如图1所示[1-4]。当变频器工作在过调制区时，矢量合成方法类型较多，导致其控制结果也有差异，其中部分控制方法按照比例减小非零矢量作用时间，强迫使零矢量的作用时间大于0，但结果不够精确。

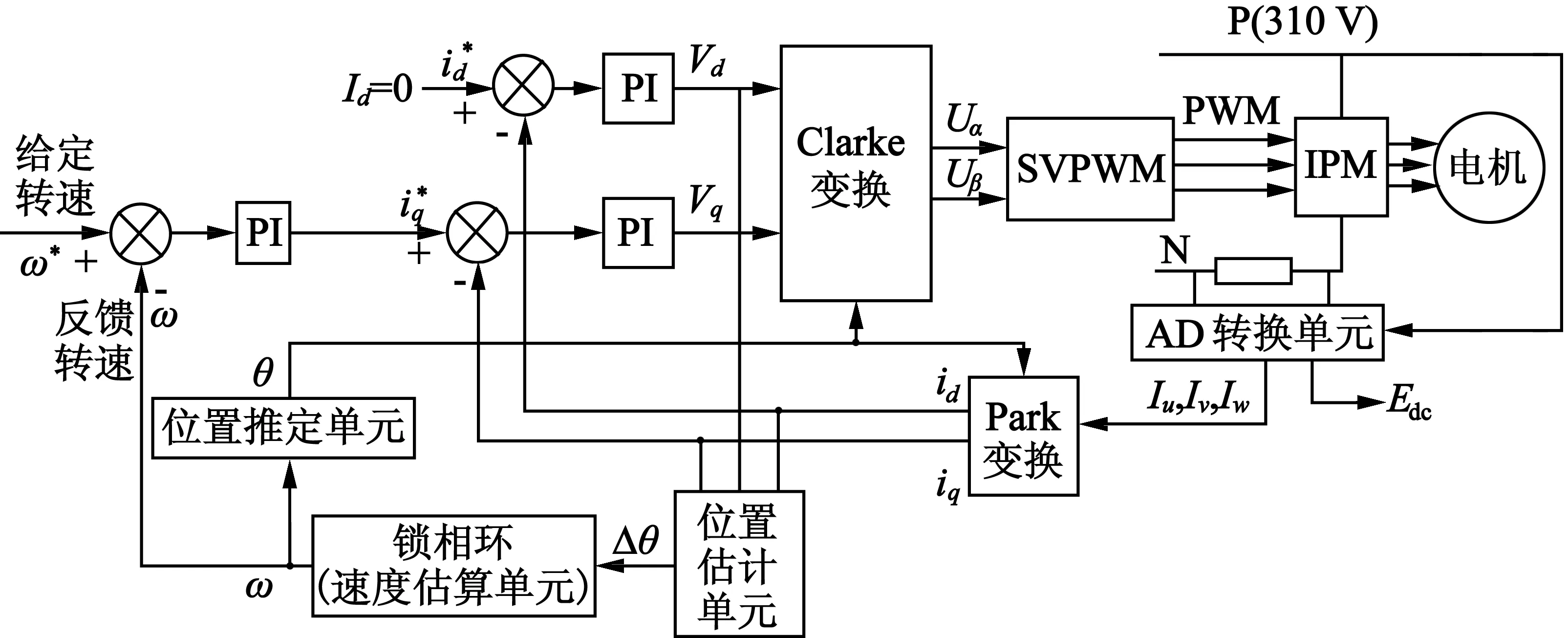
图1SVPWM控制系统框图

目前变频电机矢量控制方法存在结果精确度差缺乏清晰理论框架的问题[5-8]。本文对SVPWM控制进行优化创新，控制方案如图2所示，对传统的空间矢量合成，计算PWM波占空比方法SVPWM，采用AVR和谐波注入方法代替，明确调制输入的函数表达式，采用傅里叶变换技术,获得三角波调制逆变器输出电压的基波幅度，按照比例关系求出d，q轴电压进而获得PWM波占空比，通过傅里叶分析和谐波注入，推导出严格的过调制I和过调制II公式，获得清晰明确的控制模型，进行诸如基波注入减小噪声等研究。

图2SVPWM优化控制方案

1 过调制控制方法

变频器调制通常采用锯齿波或者三角波调制，用得最多的是三角波调制，通过对调制后的波形进行傅里叶分析，获得输出波形vao的基波傅里叶函数表达式：

(1)

式中：vp为调制波峰值；vT为三角波峰值；vd为母线电压；ω为角频率。

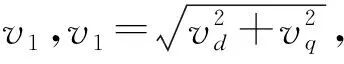
(2)

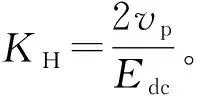
(3)

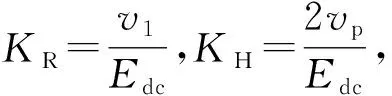
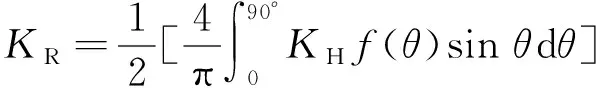
(4)

式中：-1≤KHf(θ)≤1。

(5)

图3谐波注入波形图

从图3明显看出，谐波注入后，压低了电压峰值，能够提高电压利用。

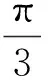
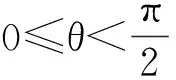
在线性区，因为-1≤KHf(θ)≤1，且：

(6)

结合式(5)和式(6)，可得:

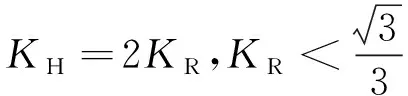
(7)

在过调制I区和过调制II区，利用式(4)可得KH～KR的对应关系表，综合利用式(7)和过调制关系表，就能进行过调制控制。

2 过调制基波及控制理论分析

2.1 过调制控制方法表达式

传统的过调制控制方法，在矢量超出正六边形时，需要将超界的电压矢量控制在到正六边形上[5]，不能保证相角完全跟随[7],按比例减小非零矢量的时间[9]，多电平 SVPWM 的过调制算法[10]。过调制模式Ⅰ引入补偿因子λ，补偿了系统在过调制区域的损失；在过调制模式Ⅱ中，引入简化“压频”计算方法，均引入了近似，模型复杂，致使控制理论不够清晰，且其相应的公式推导不严谨。

针对传统的空间矢量合成计算PWM波占空比方法SVPWM无清晰表达式的缺点，工程技术人员反复研究提出了不同的控制模型和控制方法，如将SVPWM算法原始的复杂计算被整数加、整减、截断等代替，但计算会带来近似，带来累计误差，而针对五相电压型逆变器(以下简称VSI )在过调制区的空间矢量调制(以下简称SVM )而提出的解决方案[11-12]，适用于高压场合。本文采用AVR和谐波注入方法代替，明确调制输入的函数表达式，采用傅里叶变换技术,获得三角波调制逆变器输出电压的基波幅度，按照比例关系求出d，q轴电压进而获得PWM波占空比，通过傅里叶分析和谐波注入，构建出严格的过调制控制公式及方法，获得清晰的函数表达式，提高过调制控制精度；同时，也可以进一步利用函数表达式进行高次谐波研究、噪声消除等领域的研究。

2.2 过调制傅里叶变换

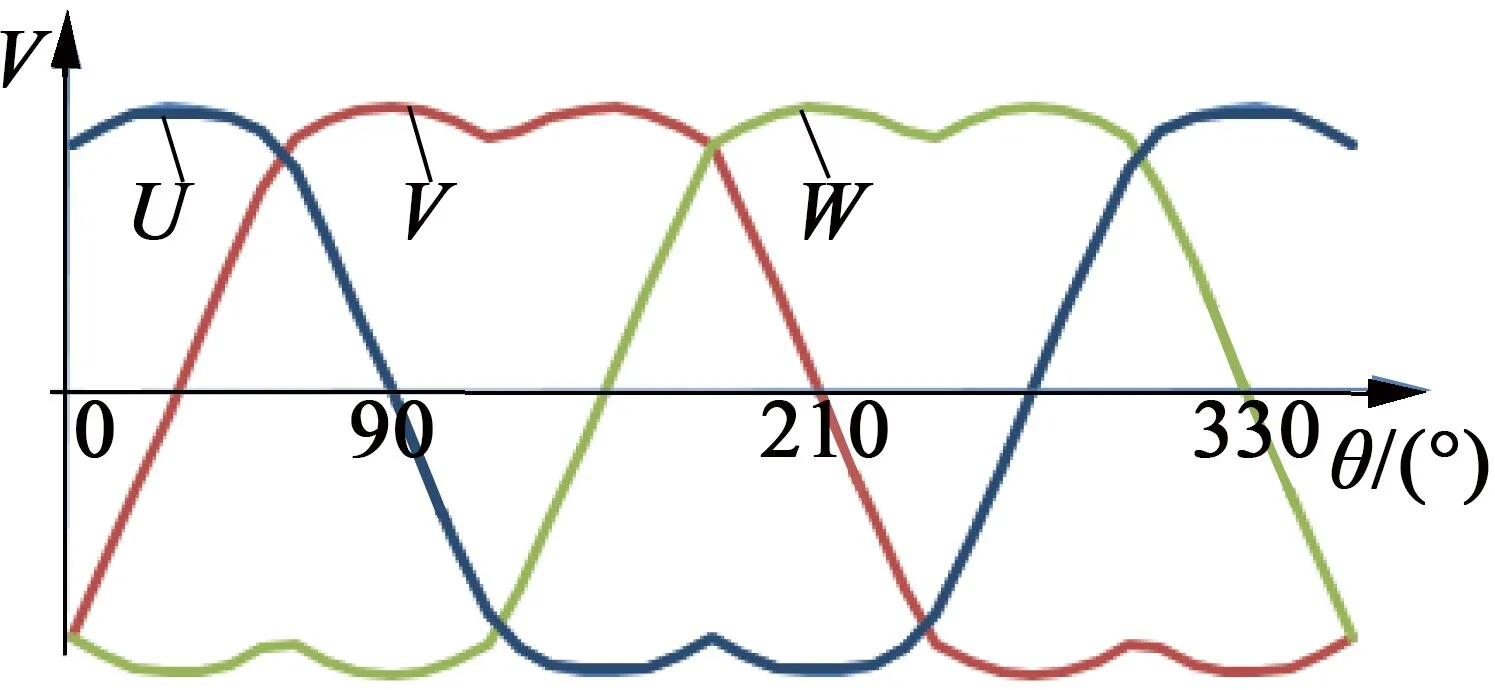
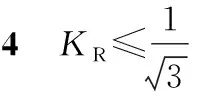
调制后的三相电压函数表达式如下：

(8)

过调制区细分为过调制I区和过调制II区。

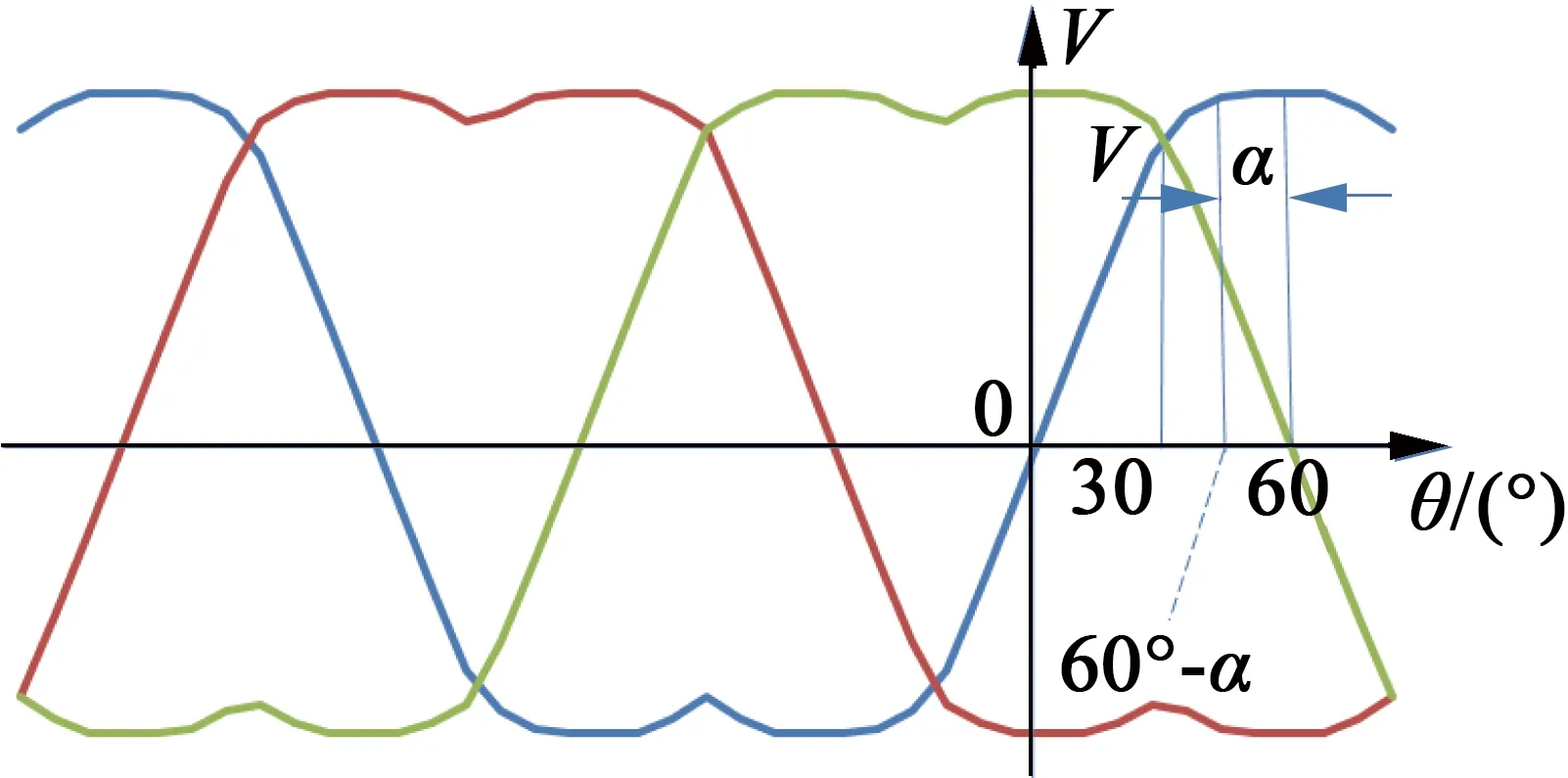
图5过调制I区调制函数波形图

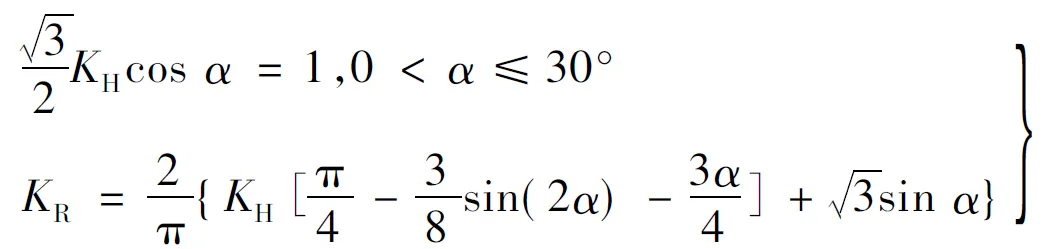
(9)

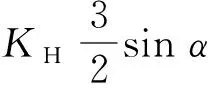
图6过调制II区调制函数波形图

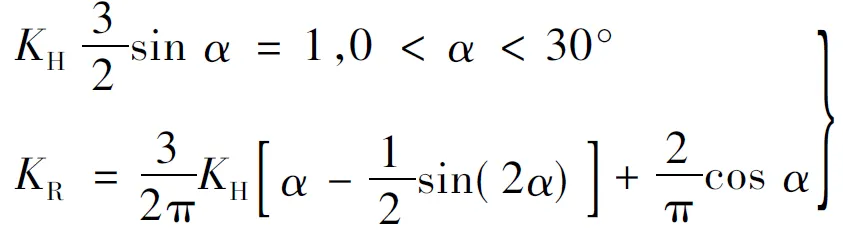
(10)

式(7)、式(9)、式(10)是KH～KR清晰的函数表达式。图7是过调制控制曲线KH～KR关系图，图7(a)是过调制时KH～KR关系，图7(b)是整个调速范围内KH～KR关系。

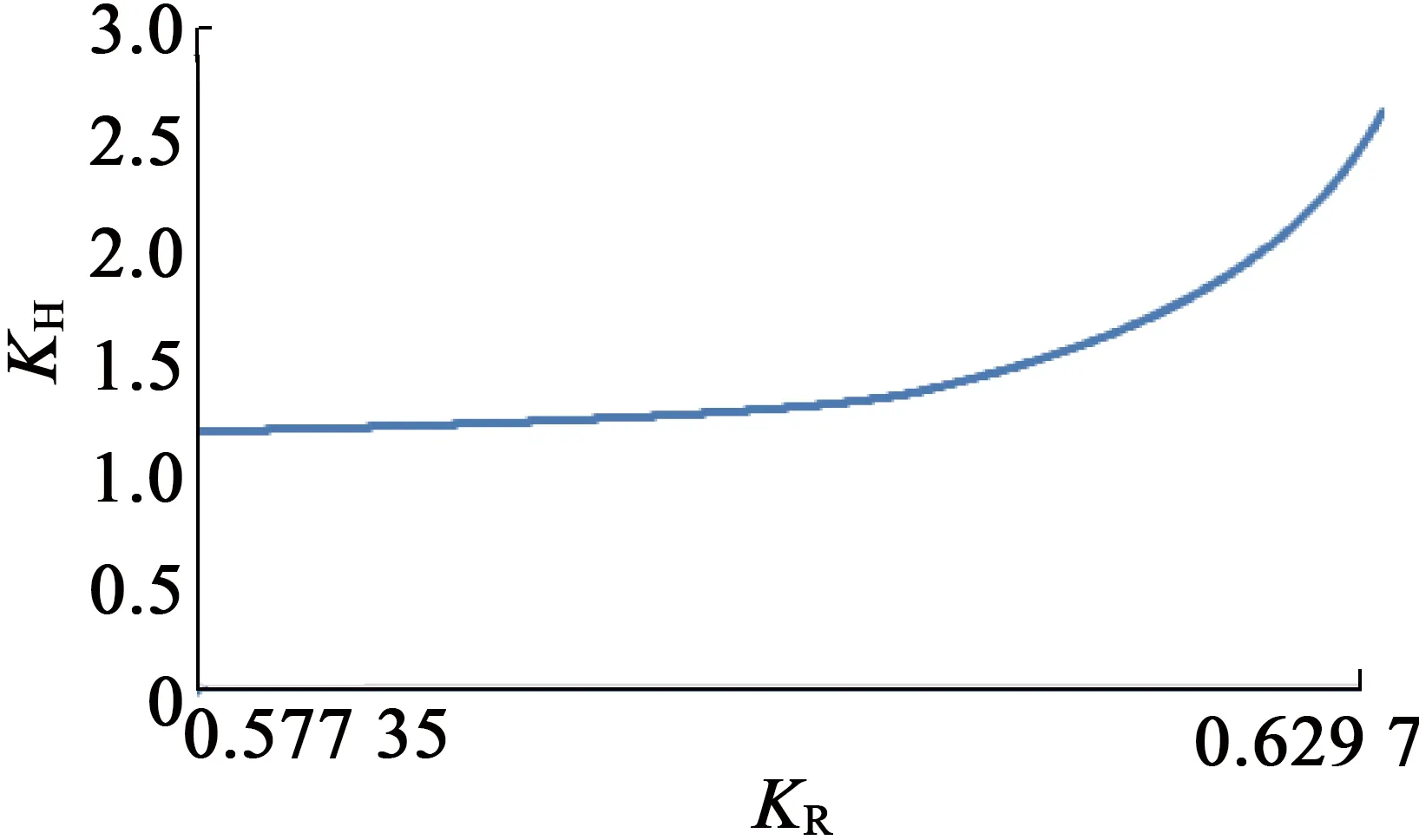
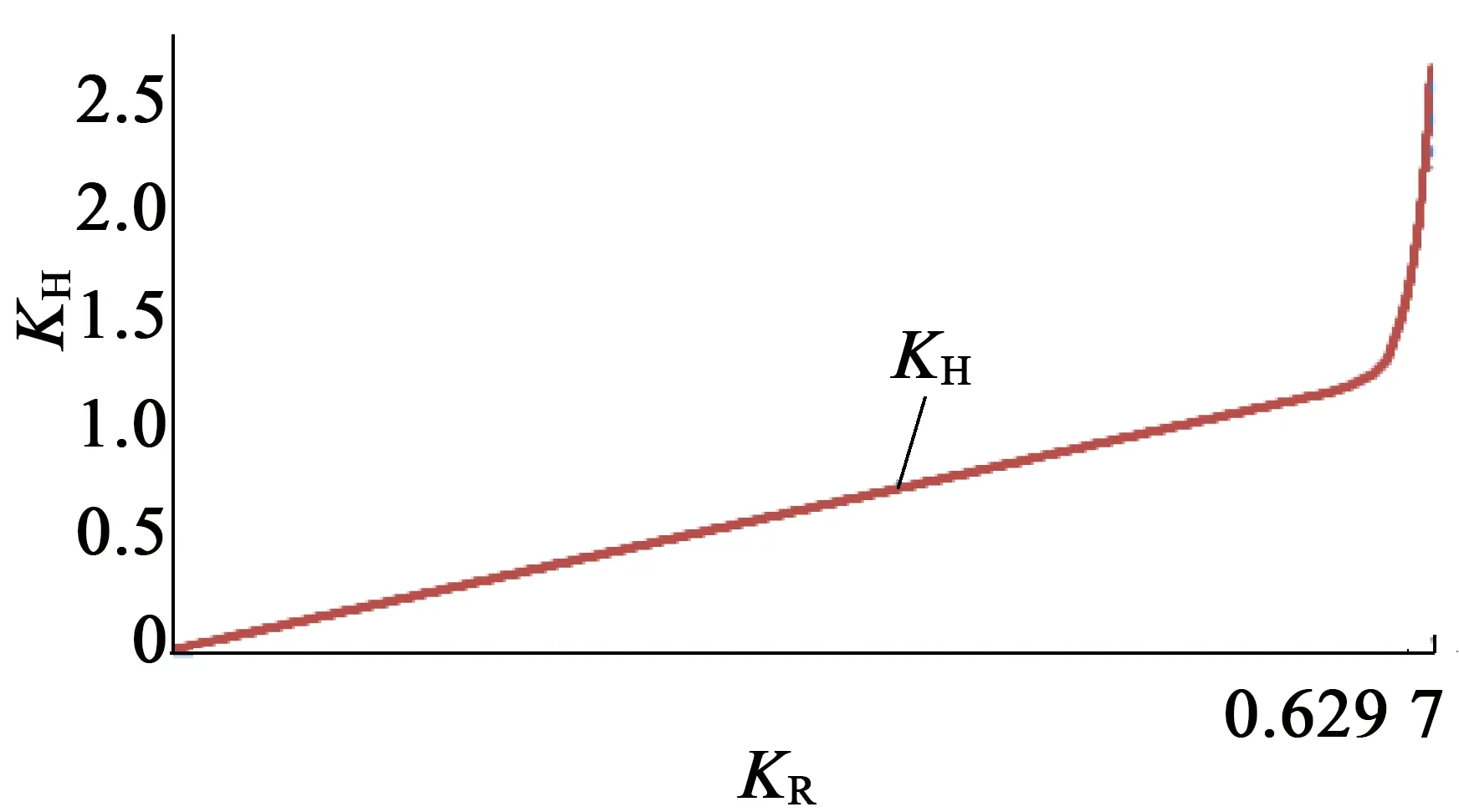
图7过调制区KH～KR关系示意图

3 过调制控制优化理论验证

3.1 过调制控制理论仿真分析

为了验证基于调制波电压基波幅值过调制控制技术的正确性，特建立如图8所示的仿真模型。

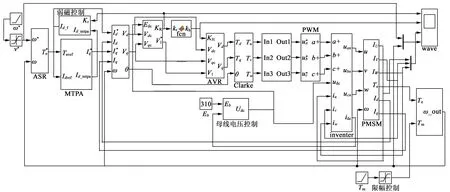
图8过调制控制MATLAB仿真模型

仿真采用上海日立电机，型号为ASD102SF-A7JT，电机参数取值：R=0.37 Ω,Lq=0.015 34 H，Ld=0.009 84 H，J=6.76×10-4kg·m2，Ke=0.091 9V/(rad·s-1),4极。频率命令以电频率(电频率等于机械频率乘以极对数)为500 Hz/s的加速度上升，建立如图7(b)所示的KH～KR关系表，波形如图9所示。其中KH和KR为归一化数值，无单位。

(a) 目标频率100 Hz仿真波形

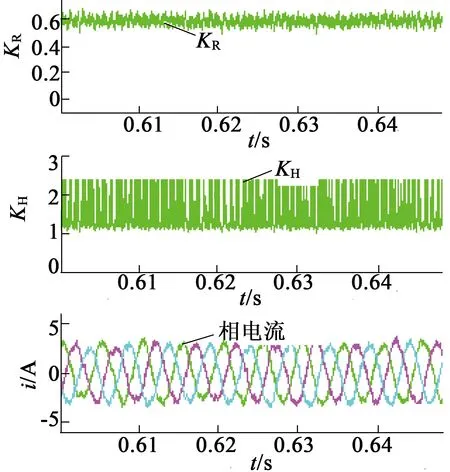
(b) 目标频率200 Hz仿真波形

图9过调制仿真图

图9(b)KH的密集程度，明显可见，图9(b)进入过调制II区的时间大于图9(a)，因为电流更大,运行频率更高,需要的PWM波占空比更大。从图7(b)可见，进入过调制后，随着KR的增加，KH几乎成指数函数关系增加，表面进入过调制后，由于电压超过正六边形，需要更大的PWM波占空比才能等效出需要的控制电压。

3.2 过调制控制理论应用案例分析

(11)

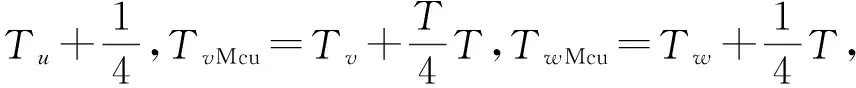
3.2.1冰箱控制系统应用案例

由于冰箱系统功率低，很难进入过调制，采用降低母线电压的方法提高KR数值。所用电机参数：R=10 Ω,Ld=0.084 22 H，Lq=0.137 15 H，Ke=0.118 23 V/(rad·s-1),J=1.6×10-4Kg·m2，电机极数p=6。在交流输入电压为130 V时，通过对冰箱电机加负载，获得电机KR、KH，注入谐波后的PWM波占空比(PWM波占空比、KR和KH采用数模转换即D/A转换输出)和电机其中一相的电流波形，如图10所示。

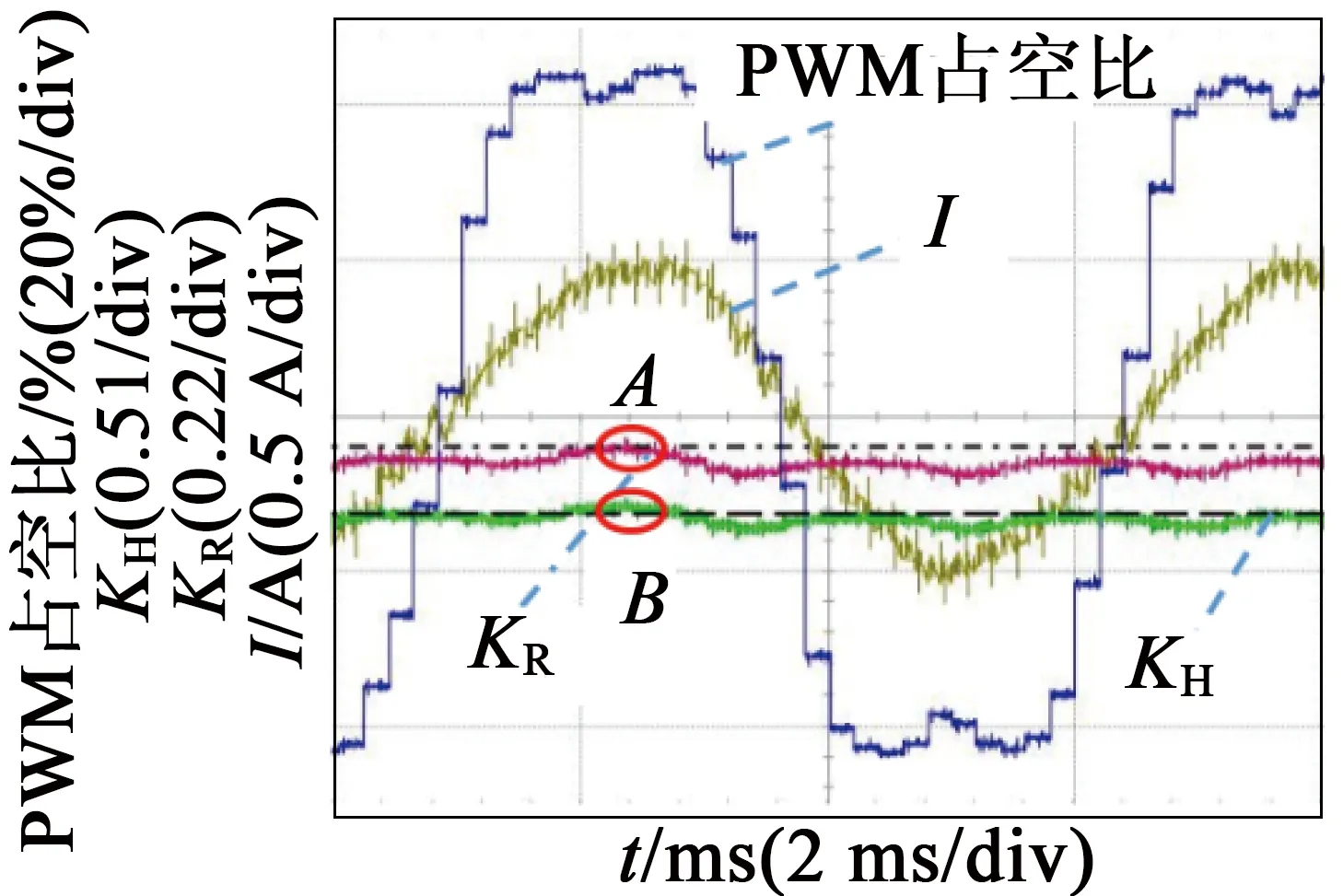
(a) 线形区波形

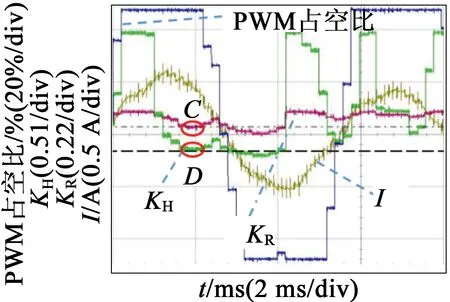
(b) 过调制区波形

图10冰箱控制系统实测波形图

图10(a)代表电机工作在线性区，谐波注入后的波形类似于图4的波形，没有消去顶部类似“M”的部分。图中A点代表的KR=0.49，B点代表的KH=0.98，KH刚好是KR的2倍。

图10(b)代表电机工作在过调制区，谐波注入后的波形类似于图6的波形，占空比顶部类似“M”的部分被消去。图中C点代表的KR=0.58，B点代表的KH=1.18，过调制区KH～KR关系曲线满足图7(a)关系，不再满足KH=2KR线性关系。

3.2.2吸油烟机控制系统应用案例

采用降低母线电压的方法提高KR数值。所采用的电机参数：R=28.4 Ω,Ld=0.11 H，Lq=0.115 H，Ke=0.205 V/(rad·s-1),J=0.112 kg·m2，电机极数p=4。在交流输入电压为161 V时，通过调节吸油烟机电机转速的方法，获得电机注入谐波后的PWM波占空比(PWM波占空比、KR和KH采用数模转换即D/A转换输出)和电机其中一相的电流波形，如图11所示。

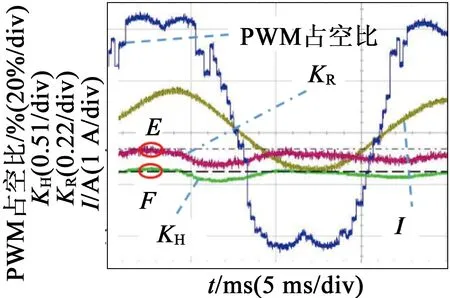
(a) 线形区

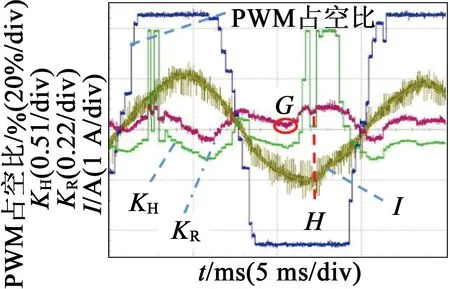
(b) 过调制区

图11吸油烟机控制系统实测波形图

图11(a)代表电机工作在线性区，谐波注入后的波形类似于图4的波形，没有消去顶部类似“M”的部分。图中E点代表的KR=0.46，F点代表的KH=0.92，KH刚好是KR的2倍。

图11(b)代表电机工作在过调制区，谐波注入后的波形类似于图6的波形，占空比顶部类似“M”的部分被消去。图中G点代表的KR=0.58，刚好进入过调制，随后，随着KR的增加，KH快速增加，虚线H处KH的快速下降，是由于KR的快速下降引起的，由于采用D/A方式输出，D/A输出有延迟和输出时间间隔限制，而且控制板上有滤波电容，造成KR在短时间内的下降，在示波器上不容易观察到；而KH能够观察到快速下降的原因是KH下降的幅度远远大于KR的下降幅度。过调制区KH～KR关系曲线满足图7(a)关系，不再满足KH=2KR关系。

4 结 语

本文针对传统SVPWM过调制矢量模型复杂，且多种控制方法控制不精准问题，进行了过调制模型研究和谐波函数的设计，并进行了傅里叶分析，获得过调制I区和过调制II区以及线性区，输出电压基波成分清晰的函数表达式。通过归一化比值KR，建立KH～KR关系，根据KR值大小，采用对应的线性调制和过调制，并采用坐标变换，及时准确地计算获取Tu，Tv，Tw，用于产生相应的控制PWM波，控制6只逆变器上/下桥臂的开通和关断。实现对永磁无刷直流电动机的精确控制，过调制由式(9)、式(10)给出了KH～KR关系，获得了准确的过调制算法和公式。

通过仿真分析冰箱和吸油烟机控制系统的实验，以及图10、图11的相电流波形平稳，证明了控制模型和过调制控制理论的正确性、技术可靠性。

此算法已在某空调品牌自主开发的180°永磁无刷直流电动机家用空调控制器上采用并投入批量生产；同时，此设计模型、算法和控制软件也在中央空调3P、5P及10P空调系统和室内外风机、冰箱和抽油烟机上广泛使用，为该公司芯片的自主设计打下了坚实的技术基础，掌握了芯片定价的主动权，打破了国外变频技术的垄断和漫天要价的尴尬局面。