基于图像理论的永磁体涡流损耗计算方法
阳喜成,师 蔚
(上海工程技术大学,上海 201600)
0 引 言
在永磁电机中由于电机齿槽的存在,定子磁动势的非正弦分布及定子绕组相电流有高次谐波等各种因素的影响,从而会在气隙磁场中产生空间和时间谐波分量,这些谐波成分会在转子永磁体产生涡流损耗[1-2]。在一些高密度永磁电机中转子的散热条件苛刻,温度损耗会导致永磁体有较大的温升,严重时将导致永磁体的不可逆退磁,影响电机的正常工作[3-4]。
在永磁电机永磁体涡流损耗的研究中,主要有解析法、二维及三维有限元法。文献[5-7]给出了考虑槽口效应的永磁体涡流损耗解析计算方法,但是均无考虑相电流引起的时间谐波对永磁体涡流损耗的影响。文献[8]通过二维有限元法分别求解了空载和负载时永磁体内的涡流损耗。文献[9]利用二维有限方法得到了一个考虑开槽效应的永磁体涡流损耗分析模型。然而二维有限元方法计算永磁体涡流损耗时无法考虑永磁体涡流损耗轴向分布的不均匀。为了改善二维有限元法的缺点,文献[10-11]利用三维有限元法对永磁体的涡流损耗进行研究,克服了二维有限元法无法计及轴向不均的问题,提高了计算精度,但三维有限元法计算时间随电机体积的增大而变长。本文针对永磁同步电机永磁体涡流损耗,研究了一种基于图像理论的三维解析法,此方法同时考虑空间谐波和时间谐波,能够快速准确地计算得到永磁体的涡流损耗值,既能保证精度,又能节约大量的时间。最后,通过建立三维有限元电机模型对本方法进行验证。
1 涡流源图像理论
根据法拉第电磁定律,给定时刻磁体中的涡流密度J取决于磁通密度B随时间的变化率,可以看作是由S表示的源分布[12],关系式可表示:
×J=σS
(1)
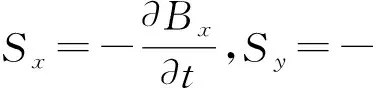
×A=J
(2)
2A=-σS
(3)
如图1所示的永磁体,x表示切向方向,y表示径向方向,z表示轴向方向,磁体在3个方向上的尺寸分别l,b,h。温度场由二维时变磁场引起,通过忽略任何曲率效应,磁体近似为矩形。磁通密度具有与z分量无关的x分量和y分量,因此,源矢量S仅具有两个分量Sx和Sy。
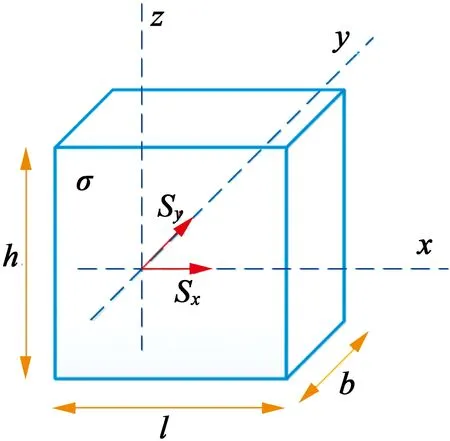
图1永磁体涡流场示意图
为了将永磁体三维涡流场与永磁体6个边界面相结合,涡流场激励源S1(x,y,z) 位于永磁体内部,如图2所示。原始源和映射图像源的图案将被扩展到无限三维空间,图像分别分布在x,y和z方向,3个矢量分量具有相同的幅度,方向垂直于边界平面的矢量分量将具有与源相同的符号,另外2个矢量分量具有与源相反的符号。然而,如果磁场是二维的,则只需要考虑2个分量。由原始源和7个图像组合的图像首先经过右xz平面反射、再经过上yz平面反射及最后经过前xy平面反射形成第一反射组合源,在0 图2以永磁体6个边界面为边界条件时的图像源分布 (4) 式中:Kx=+i-j;Ky=-i+j;Kz=-i-j;r1,r2,r3,r4,r5,r6,r7,r8分别为原始源和各个映射源在三维坐标系中所处位置的域空间。 r1:0 r2:0 r3:l r4:l r5:0 r6:0 r7:l r8:l 原始源和边界条件在6个平面的组合效应最终得到的等效源S3-D(x,y,z,t)以三维周期形式表示: (5) 由原始源和边界条件在6个平面组合效应的数学表达式可知,永磁体内的涡流源分布可以进行三维傅里叶分解,得到涡流场信息的三维空间分布,进而可以得到考虑空间谐波的永磁体涡流损耗数学模型。 采用时间步进的二维有限元分析方法,可以得到转子磁体中的磁饱和,开槽和空间谐波的涡流源分布,进而可以通过以下形式的三维傅里叶级数展开为三维空间: (6) (7) 式中:m,n,k分别是x,y,z方向的谐波阶数,涡流源系数a(m,n,k)和c(m,n,k)通过对涡流源进行三维傅里叶分解得到。三维傅里叶变换是建立在永磁体的边界条件和×A=0的基础上。式(6)和(7)意味着磁体内的源分布在三维空间中周期性地重复,由满足式(3)泊松分布的式(6)及式(7)可以得到电流矢量势切向分量Ax和径向分量Ay的分布如下: (8) (9) 式中:d(m,n,k)和e(m,n,k)是与(m,n,k)次谐波有关的矢量电势系数。根据式(2)可以得到涡电流密度的切向分量Jx径向分量Jy以及轴向分量Jz如下: (10) (11) (12) 式中:系数h(m,n,k),q(m,n,k),p(m,n,k)分别为x,y,z方向上的涡流密度系数,可以根据a(m,n,k)和c(m,n,k)推导出来。 根据涡流分布,给定时刻空间谐波产生的总涡流损耗就是与每个谐波分量相关的损耗之和: p3(m,n,k) +p4(m,n,k) +p5(m,n,k)] (13) 式中:p1~p5为永磁体尺寸和所有谐波阶数的算术函数,表示永磁体总涡流损耗。 p1(m,n,k) =c2(m,n,k)· p2(m,n,k) =a2(m,n,k)· p3(m,n,k) =c2(m,n,k)· p4(m,n,k) =a2(m,n,k)· 除了定子开槽等产生的空间谐波会在永磁体上感应出涡流效应,电机激励源输入的PWM波相电流也会在永磁体上感应出涡流损耗。某特定频率下单位体积永磁体的涡流损耗数学模型可表示[13]: (14) (15) 式(13)和式(15)分别是考虑空间谐波和时间谐波的永磁体涡流损耗数学模型。因此,同时考虑空间谐波和时间谐波的总涡流损耗数学模型: p3(m,n,k) +p4(m,n,k) +p5(m,n,k) ]+ (16) 将上述的三维解析法应用于一台90 kW,48槽8极的内置式永磁电机,用于计算转子永磁体上的涡流损耗,原型电机的参数和材料属性如表1所示,电机模型如图3所示。 表1 电机基本数据 图3永磁电机模型 通过采用广义图像理论分析,给定时刻磁体中的涡流密度J取决于磁通密度B随时间变化率的原始源S1(x,y,t)和边界条件的组合效应可以由S3-D(x,y,z,t) 表示,其在x,y和z向上是周期的。 为了能够得到原始源S1(x,y,t)的信息,需要在永磁体上构建网格来提取磁密值形成磁密矩阵,矩阵中的磁密值应该对应于连接到磁体的x-y坐标给定位置处的源。考虑到电机在圆周方向的对称性,可以仅在电机一极的永磁体上进行手动划分后构建网格,网格上的每个交点都会形成涡流场信息的x和y坐标。x方向和y方向的离散数量决定了涡流分布的准确性,离散的数量越多,则涡流场分布的准确度越高。 然而,由于捕获的磁通密度值(Bx1和By1)是在初始转子位置处附着于磁体的静态(x1和y1)坐标系中提到的, 因此需对这些值进行变换,确保涡流源(Sx1=-∂Bx1/∂t和Sy1=-∂By1/∂t)在转子坐标系中被引用。从而,相对于在时间t附着于永磁体的旋转坐标系(xr1和yr1)的角位置ωt处的通量密度值(Bxr1和Byr1)可以表示: Bxr1=Bx1cos(ωt)-By1sin(ωt) (17) Byr1=Bx1sin(ωt)+By1cos(ωt) (18) 涡流源(Sx,Sy)可以通过二维有限元法在两个连续时间间隔得到的磁通密度值来获取,再通过分别对Sx和Sy进行三维傅里叶变换,可以得到涡流源系数a(m,n,k)和c(m,n,k),其中,m,n,k分别是x,y,z方向的谐波阶数。 为了考虑时间谐波对永磁体涡流损耗的影响,采用从现场测试实验输入永磁电机的PWM波进行计算,电流波形如图4所示。 图4PWM波相电流波形图 因此,得到了同时考虑空间谐波因素和时间谐波因素的永磁体涡流损耗。 永磁电机分别运行在额定工况和峰值工况下,利用有限元软件对电机不同转速的永磁体涡流损耗进行仿真计算。表2比较了两种方法在不同工况不同转速下的涡流损耗值,从表2中可以看出,有限元结果与解析法结果之间具有良好的一致性。因此,上述所提出的基于图像理论三维解析法具有较高的精度,同时,由于解析法是利用二维模型提取的涡流信息,并且计算过程都是在MATLAB软件中进行,能够快速地得到想要的结果,所以在计算时间上相比较与三维有限元法具有一定的优势,并且能够保证精确度,由此可以证明此方法的准确性及可行性。 表2 有限元法与解析法结果对比 本文基于三维涡流场图像理论,研究了一种可有效计算内置式永磁体电机永磁体涡流损耗的三维解析方法。这种方法考虑开槽效应,磁体内部的径向和切向场变化以及不同源谐波的相互作用,同时,也考虑定子相电流的高次谐波的影响。由于它是采用二维有限元法来提取电机的磁通密度值,所以本文的三维解析法考虑了电机的磁饱和效应。并将此方法运用到一台8极48槽的内置式永磁体电机永磁体的涡流损耗分析上,最后通过有限元软件建立电机的三维模型对其进行验证,证明该方法具有较高的精确度及可行性。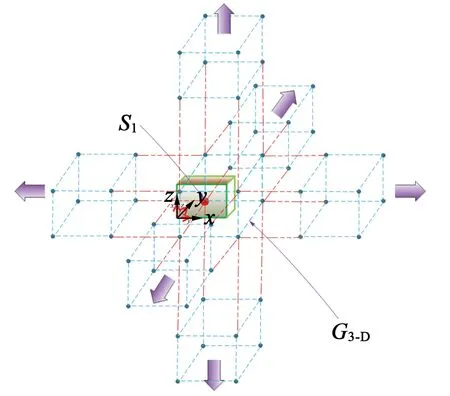
2 涡流损耗数学模型
2.1 考虑空间谐波时涡流损耗数学模型
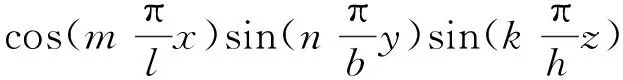
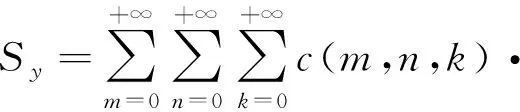
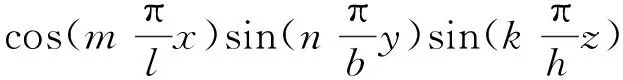
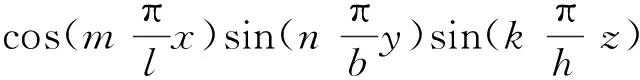
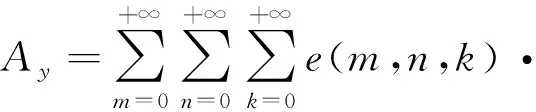
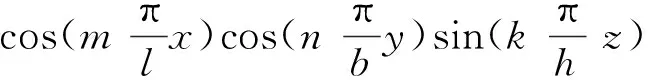
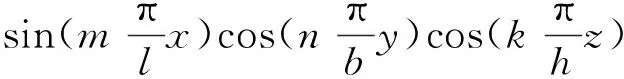
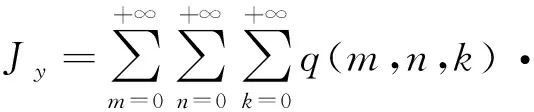
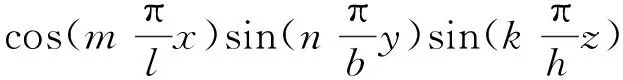
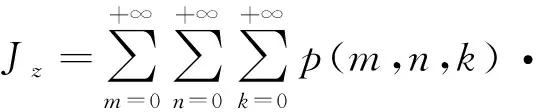
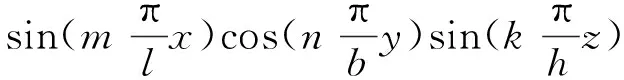
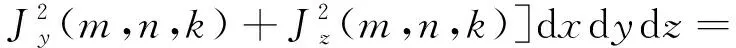
2.2 考虑时间谐波时涡流损耗数学模型
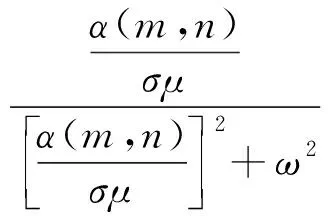
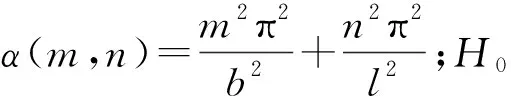
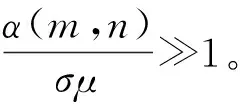
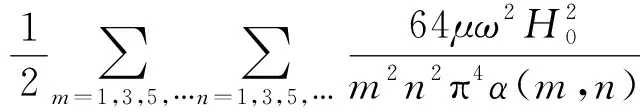
3 计算分析
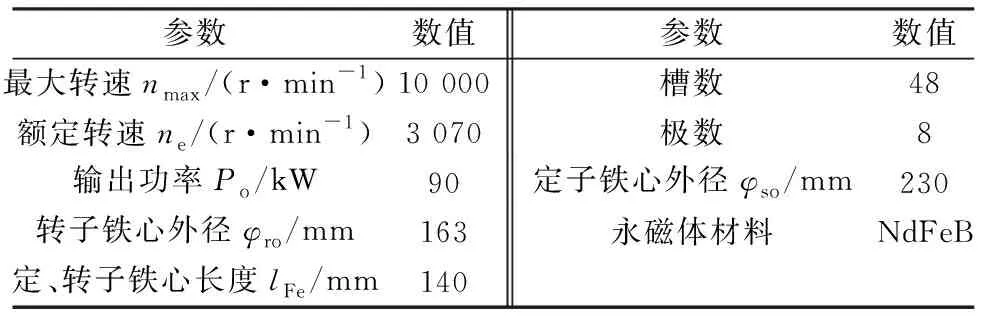
3.1 永磁电机参数
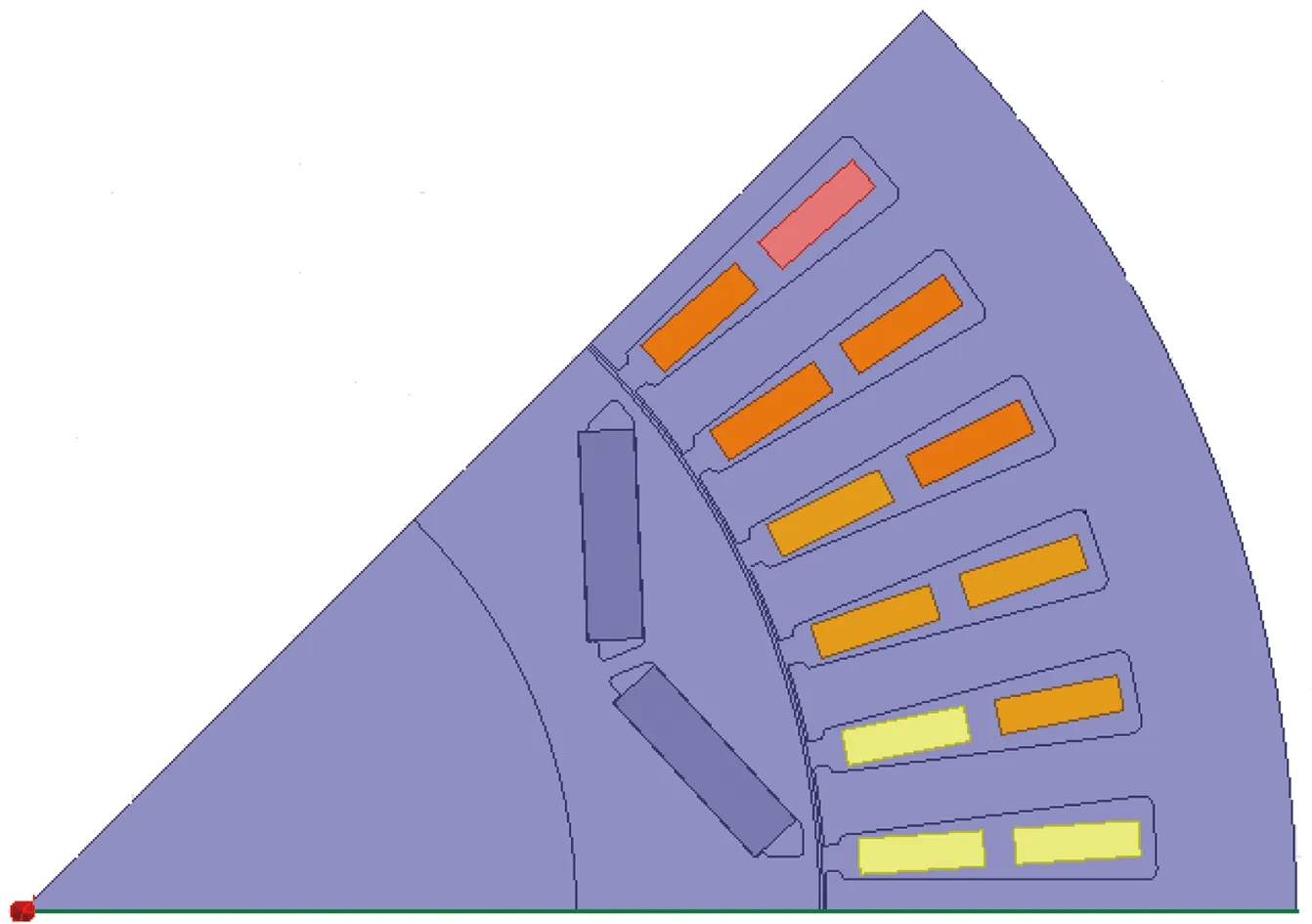
3.2 二维有限元法提取涡流场信息
3.3 PWM波电流

3.4 有限元法与解析法结果比较

4 结 语

