基于PWM电流微分的同步磁阻电动机无传感器控制

吕艳博，郝 成，陈 赛，宋文超

(华北理工大学，唐山 063210)

0 引 言

同步磁阻电动机(以下简称SynRM)转子没有电磁损耗，比异步电动机更简单坚固，不存在转子发热等问题；与开关磁阻电动机相比不存在噪声及运行时转矩脉动大等问题；能避免永磁同步电动机高温失磁的问题。因而SynRM具有较大的实际应用价值和较高的发展潜力。

SynRM控制的重要环节就是转子的位置检测。传感器检测技术及无位置传感器检测技术是两种常用的位置检测方法，而机械传感器在SynRM中的应用，增大了控制系统的成本和结构的复杂性，并且在高温、高压或者电磁扰动环境中，限制了传感器的使用，进而限定了它的应用场合。因此无位置传感器技术有良好的应用前景[1-3]。

文献[4]提出无位置传感器技术缩小了系统尺寸，减少了系统成本，代表了未来发展趋势；但存在控制算法复杂，精度难以保证，起动困难，动态性能不理想，运行转速范围小等缺点。文献[5]根据同步电机的结构特点，提出在励磁部分注入高频信号从而进行位置和速度检测的方法；但该方法的缺点是高频信号的选取过程比较复杂，需要考虑许多方面的因素，并且转子磁极的判别需要再次注入其他形式的信号。文献[6]介绍了一种基于PWM载波信号的无位置传感器技术，不需要判断转子磁极，但对高频信号的提取、处理和计算比较复杂。本文研究了一种基于PWM电流微分的SynRM转子位置角检测方法，并构建无位置传感控制系统。和以往高频信号注入法的不同之处在于，此方法将逆变器自身的载波频率信号作为高频输入信号，不用二次引入高频信号，有效地改善了现有初始位置检测方法中存在算法复杂和运行时间长等缺点；另外，与PWM载波信号法相比较，该方法PWM电流微分绝对值的信号强、稳定性好并且处理简单。实验表明，该方法简单可靠，有一定实用价值。

1 SynRM数学模型

SynRM由反应式电动机发展而来，其定子和普通的同步电机相同，但是转子不需要安装励磁绕组。SynRM在静止α，β坐标系下的数学模型如下[7]：

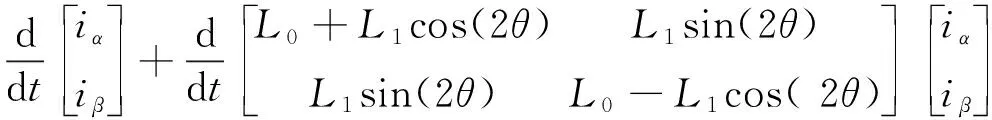
(1)

为了分析基于PWM电流微分的SynRM转子位置角的估算算法，引入另一两相静止坐标系γ,δ轴系。γ,δ轴系、α,β轴系与d,q轴系矢量关系如图1所示。

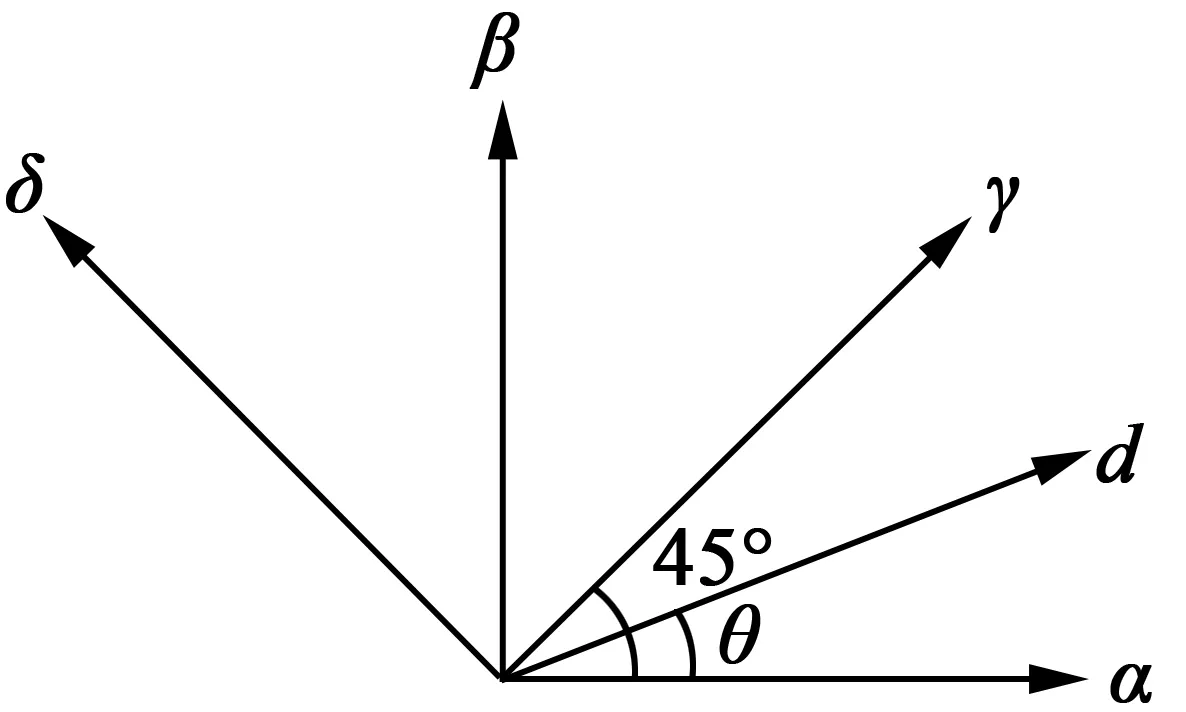
图1 三种轴系矢量关系图

则α,β坐标系变换到γ,δ坐标系的变换矩阵[8]：

(2)

由于PWM载波频率比电机基波频率高很多，所以SynRM由电阻引起的压降与由电感变化引起的压降可忽略不计。则同步磁阻电机在α,β轴系下的高频成分电压模型：

(3)

对式(3)进行变换,得SynRM在α,β轴系下的高频成分电流微分模型:

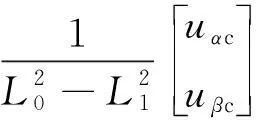
(4)

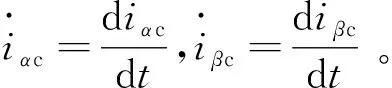
根据式(2)进行坐标变换得到γ-δ轴系下的高频成分电压与电流微分模型：

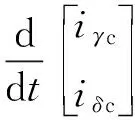
(5)

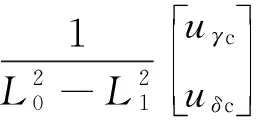
(6)

2 基于PWM电流微分的转子位置估算原理

PWM 调制所使用的调制方式是由载波和调制波组合方式所决定的，输出信号的频谱因调制方式而不同。确保系统参量中含有载波频率成分是实现载波频率成分法的前提，所以要选择合适的PWM调制方式。PWM调制方式一般有2种：一种是共用三角波调制，该调制方式下逆变器输出的线电压中不存在载波及载波谐波成分；另一种方式是三相三角载波调制，在该调制方式下，线电压中含有载波及载波谐波成分，可以用于载波频率成分法[9]。

三相三角载波调制下且当逆变器调制比很小时(电机低速或零速时)，逆变器输出的载波频率成分电压方程[10]：

(7)

此电压作为电机的高频激励信号。经过坐标变换可得电机在α-β轴系与γ-δ轴系下载波频率成分电压：

(8)

(9)

将式(8)代入式(4),式(9)代入式(6)可得：

(10)

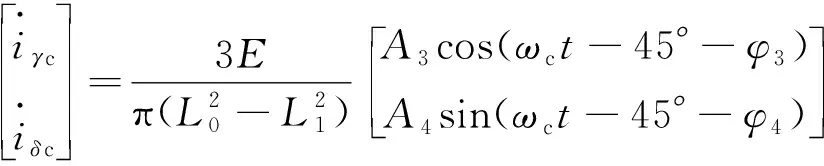
(11)

式中：

则电机在α,β,γ,δ轴上的载波频率成分电流微分峰值：

(12)

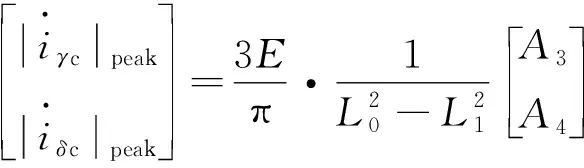
(13)

进一步推导可得：

(14)

(15)

通过以上计算，即可得出θ值，但是在计算过程中θ值会受到电压与电流信号中噪声的影响，所以采用简单易行且估算精度更高的正交锁相环来获取转子位置θ。由上文可得：

(16)

基于正交锁相环原理可以获得转子位置信息，如图2所示。定义跟踪误差函数：

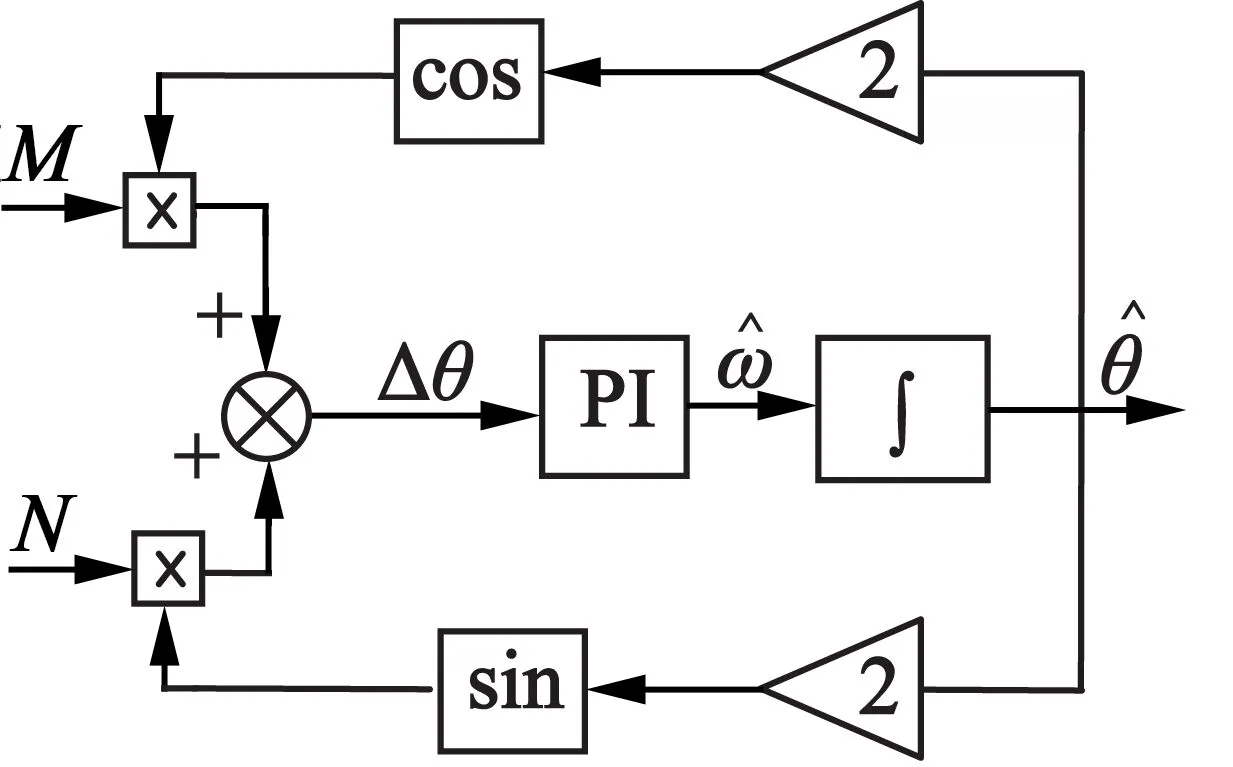
图2 基于正交锁相环的转子位置角估计框图

3 仿真实验

为了验证本文基于PWM电流微分的SynRM无位置传感器控制方案的性能是否可靠，在MATLAB/Simulink环境下搭建了仿真模型。图3为SynRM无位置传感器控制系统结构框图，通过MATLAB/Simulink软件中的S函数搭建了SynRM数学模型。

图3 基于PWM电流微分的无位置传感器控制系统结构框图

仿真设置的电机参数如表1所示。

表1 SynRM参数

仿真波形如图4、图5所示。

图4(a)为电机转速实际值与估计值对比图，图4(b)为电机转速误差曲线。由图4可以看出，该算法在起始点附近电机实际速度与估计都出现了较大振荡，但在进入闭环后两者几乎重合。图5(a)为电机转子实际位置与估计位置对比图，可以观察出两者基本吻合。图5(b)为电机转子位置误差曲线，在起始点有较大误差，但在电机正常运行时误差接近零。

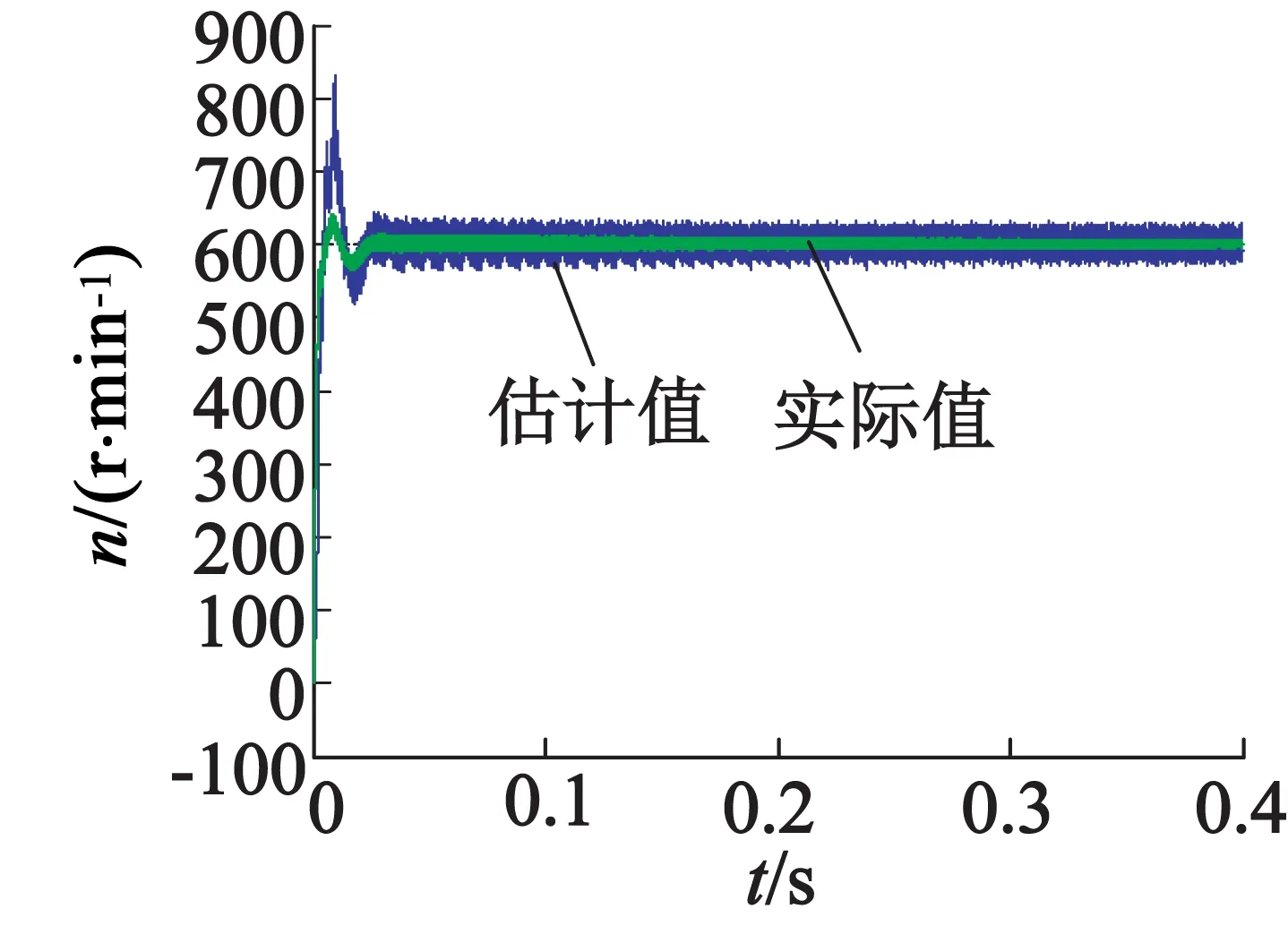
(a) 电机转速估计值与实际值

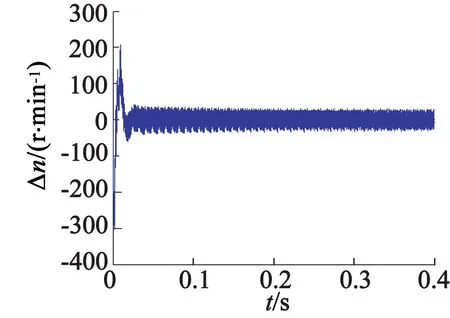
(b) 电机转速估计误差

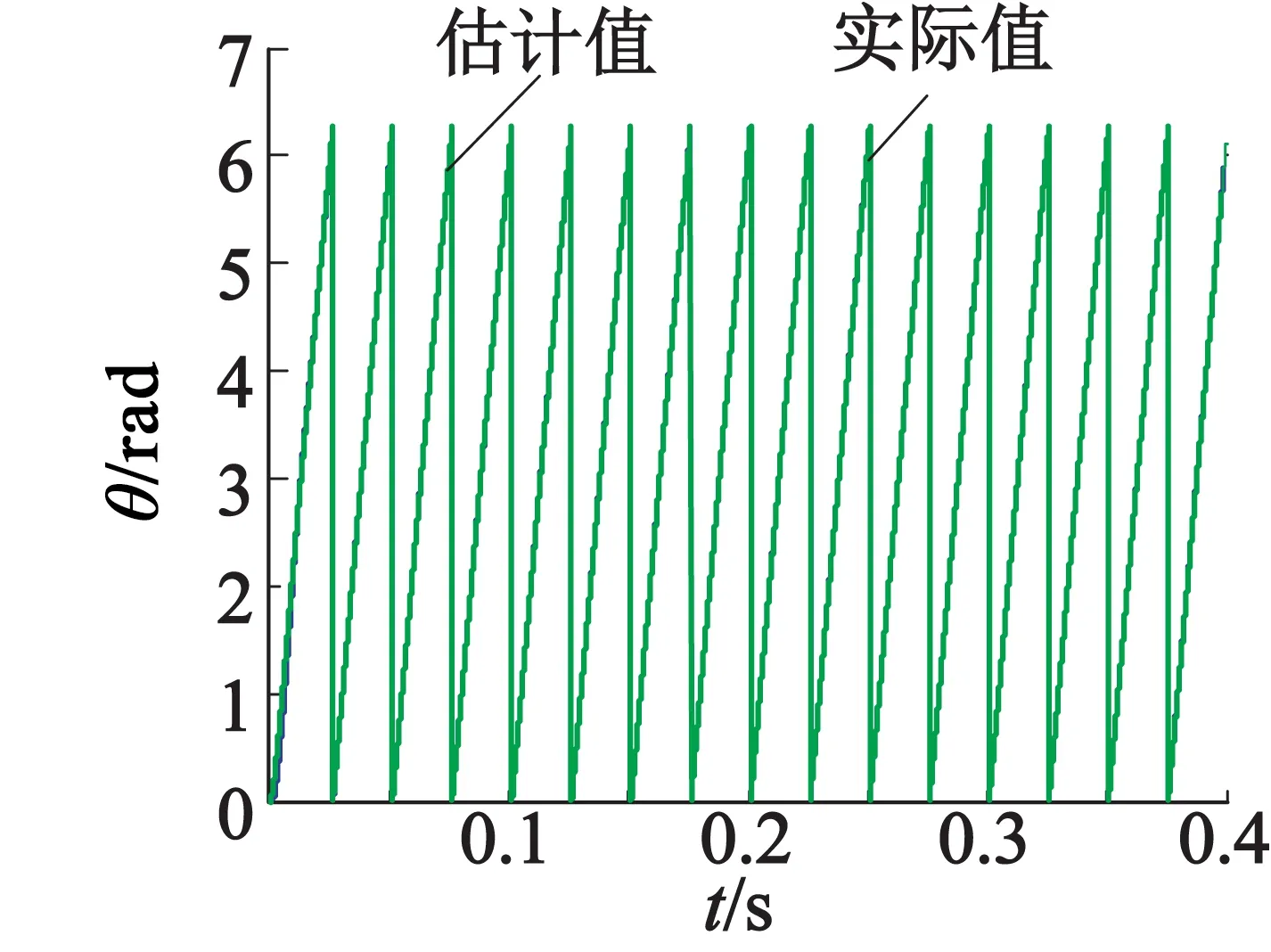
(a) 电机转子位置估计值与实际值

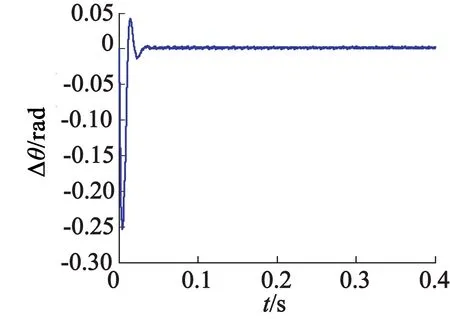
(b) 电机转子位置估计误差

4 结 语

本文针对SynRM转子位置估计的局限性，研究了基于PWM电流微分的无位置传感器控制技术，分析了转子位置信息的提取过程，并构建系统控制结构框图，利用MATLAB对系统进行仿真。解决了位置传感器受极端环境影响、高频注入法高频信号选取过程繁琐与PWM载波信号法计算复杂的问题。结果表明本文的设计对SynRM转子位置进行有效估计，系统可以稳定运行，具有较强的可行性与有效性。