永磁同步电机匝间短路-退磁耦合故障分析

王 欢，郑安文，许小伟，王苏娟，雷 鹏

(武汉科技大学，武汉 430074)

0 引 言

永磁同步电机是常用永磁电机之一，体积小、效率高、转矩密度大和功率因数大是其显著的优点。与传统电机相比，永磁同步电机因自励磁而无需电枢和滑环，减少了励磁损耗、摩擦损耗和接触电损耗，效率明显提高[1]，因而被广泛应用于混合动力汽车和纯电动汽车等新能源汽车中，但由于其运行工况复杂、安装空间狭小和散热环境恶劣等缺点，导致使用中故障率较高[2]。就使用情况而言，永磁同步电机的常见故障主要分为单一故障和耦合故障两类。

耦合故障即两种或两种以上故障同时存在，如匝间短路故障在故障发生早期不易被察觉，故障后会引起电机内部电磁场畸变，继而引发永磁体退磁故障的产生，导致电机出现匝间短路和永磁体退磁同时存在的耦合故障情形[3]。如果不及时对电机故障做出相应处理，则会出现局部温度过高，导致电机无法正常工作甚至被烧毁，不仅造成经济损失，严重时还会威胁驾驶员的生命[4]。但是目前关于永磁同步电机故障分析的研究多数集中于单一故障的研究，对耦合故障的分析相对缺乏，因此对电机的耦合故障展开深入分析具有重要的现实意义。

单一故障则是指电机只存在一种故障类型，如匝间短路故障、永磁体退磁故障、转子断条和偏心故障等。现有的对单一故障的研究主要是在匝间短路故障、永磁体退磁故障和偏心故障等方面。文献[5]以混合动力汽车用永磁同步电机为对象，研究其定子断层故障，并指出该断层在电流和电压的作用下会产生特定的畸变；文献[6]提出了一种基于模型的永磁同步电机匝间短路故障检测与隔离的方法，根据状态观测者估计的定子电流和定子电流的差产生的残余电流矢量(以下简称RCV)来实现故障检测；文献[7]以永磁同步电机的电气故障研究为主体，分别通过MATLAB/Simulink和Ansoft对相间短路、单相接地、失磁故障和匝间短路故障进行仿真模拟，并提出小波分解和神经网络相结合的故障诊断方法；文献[8]以V形磁路结构的永磁同步电机为对象，分析了单个磁极的不可逆失磁对单槽反电动势的影响，并推导出了任意单个磁极以及任意多个磁极的空载反电动势的数学模型，该数学模型可应用于不同程度的失磁故障分析中。传统的单一故障分析是建立在电机的数学模型基础上，通过计算数据分析电机的故障，计算繁琐且不能准确反映电机真实的工作状态[9]。

通过对目前研究现状的分析可知，多数研究人员采用仿真代替实验来获取电机正常及故障运行条件下数据。由于对退磁类耦合故障的实验属于破坏性实验，本研究亦通过数学模型进行验证，即在Ansoft Maxwell环境下建立永磁同步电机的二维物理模型，并进行瞬态磁场分析，准确获得电机在空载和额定负载两种工况下，正常运行情况以及各种不同耦合故障程度的电磁场分布及特征参数的性能曲线，再对相反电动势进行傅里叶变换以建立判断依据，旨在为电机耦合故障诊断提供一种简洁有效的判断依据。

1 电磁场及边界条件分析

永磁同步电机定子上装有绕组，转子上装有永磁体[10]。永磁体周围会产生磁场，定子绕组有电流通过会产生电场，继而电机会存在电场和磁场的耦合。

电磁场的求解通常归结为求偏微分方程的解，主要研究没有初始条件而只有边界条件的定解问题；其分析一般采用位函数描述，而二维电磁场计算多采用磁矢位，以方便绘出磁力线分布并求出磁通[11]。

1.1 边界条件及离散化

研究磁场问题一般用第一类和第二类边界条件。第一类边界条件是指边界上的物理条件规定了物理量u在边界Γ上的值:

u|Γ=f1(Γ)

(1)

第二类边界条件则是指u的法向微商在边界Γ上的值[12]:

(2)

二维电磁场为垂直于电机轴的平行平面场，平面场域Ω上的电磁场问题的边界条件可表示:

(3)

式中：γ为磁阻率，γ=1/μ，μ为磁导率；A为磁矢位；Jz为源电流密度；Ht为磁场强度的切向分量；Γ1,Γ2分别为第一类边界条件和第二类边界条件[13]。

二维磁场只有x和y轴分量，表达式分别如下[14]:

(4)

则式(3)可等价:

(5)

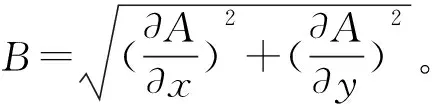
式(5)离散化后对应的非线性有限元方程组:

[k]A=p

(6)

令：{f(A)}=[k]A，按Taylor级数展开(略去高次项)后可得Newton-Lafayson迭代格式[14]:

Jk{ΔA}={Δp}

(7)

式中：{ΔA}={A}k+1-{A}k为磁位差；{Δp}=p-{f(A)}为剩余向量；Jk为第k次迭代时的Jacobin矩阵[13]，其单元计算公式:

(8)

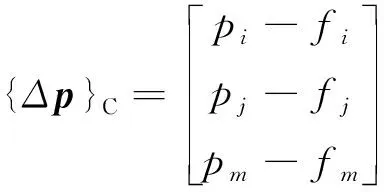
(9)

式中：

(10)

(11)

式中：Δ是离散为多个小单元时单个三角形单元的面积。

对磁化曲线的处理通常采用插值法，即用函数H=f(B)表示磁化曲线，每个插值节点Bi对应函数值为Hi(i=1，2，…，n)[12]。经线性插值法处理后可得:

显然，获得J和Δp，式(7)就可解得。

1.2 磁矢位的应用

(1)计算磁通

根据斯托克斯定理可得:

(13)

(2)计算感应电动势:

(14)

(3)画二维磁场

二维磁场中等A线即磁力线，证明如下。磁场中磁力线方程:

B×dl=0

(15)

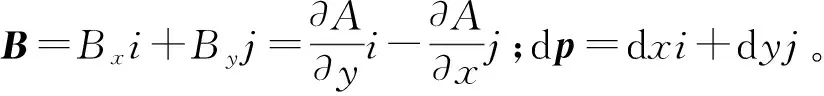
而等A线就是A=常数的轨迹，其全微分是:

(17)

这与磁力线方程完全相同，说明等A线就是磁力线。

2 耦合故障关键特征量分析

这里耦合故障是指永磁同步电机匝间短路故障和永磁体退磁故障的耦合。

2.1 永磁同步电机正常模型及故障模型建立

根据电机的尺寸参数，在Ansoft中建立正常条件下的二维有限元全模型，如图1(a)所示。永磁体呈双层V形排列，材料为NdFe35；定子绕组为双层分布短距绕组，节距为5，材料为铜；定、转子铁心材料为DW465-50，转子轴材料为steel-1010，电机结构尺寸等基本参数如表1所示。

由于自适应网格剖分的单元格比较稀疏，会导致计算结果准确性不高，为提高计算精度选择手动剖分方式。因永磁同步电机是对称结构，为减少计算，选择1/4模型进行二维瞬态磁场求解，图1(b)为永磁同步电机1/4模型在初始时刻的网格剖分图。

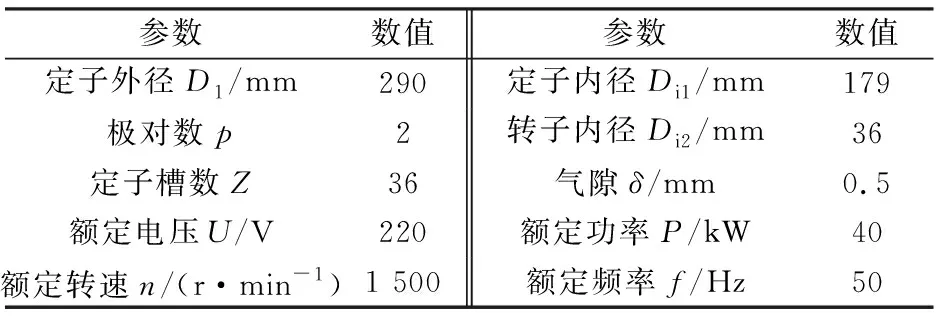
表1 电机主要参数

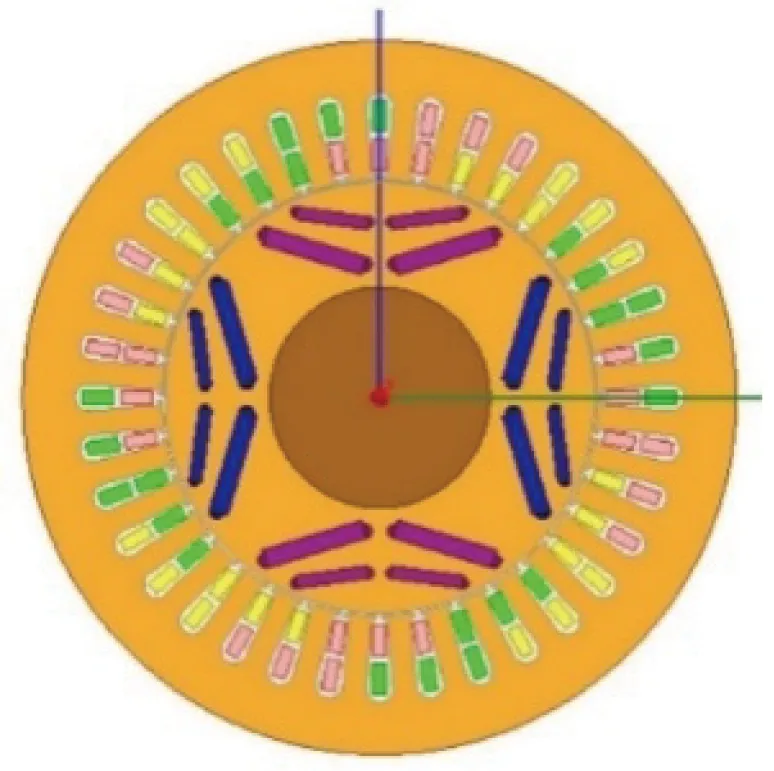
(a) 电机全模型

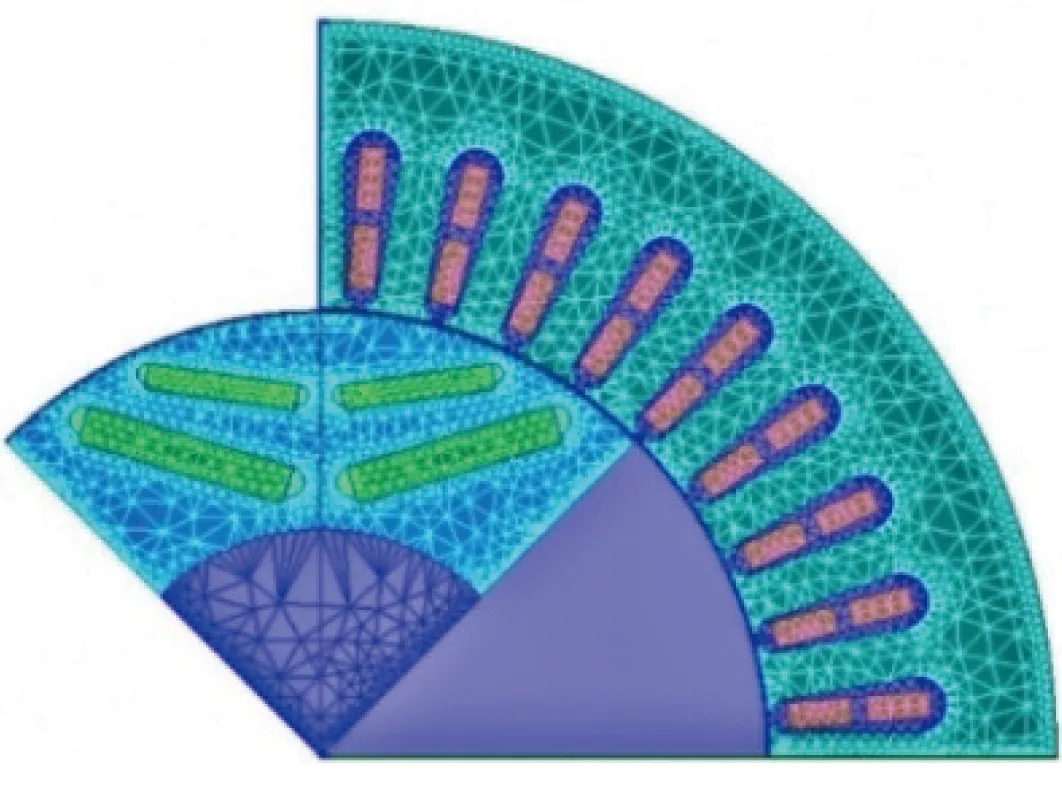
(b) 电机1/4模型在初始时刻

永磁同步电机常用的驱动电路类型有DC(直流)，PWM(光耦)，Sine Wave(交流正弦波)三种，本文采用Sine Wave供电，三相定子绕组各相差120°，如下所示：

(18)

以上建立的是电机正常条件下的有限元模型，而电机故障模型是在电机正常模型的基础上，根据故障类型的机理而改变某些参数实现的，其具体分析过程如下。

设电机的正常相串联匝数为N，A相未被短路的匝数为N1，A相被短路的匝数为N2，三者满足[2]:

N1+N2=N

(19)

根据文献[15]对永磁体材料退磁曲线的分析，得到电机发生退磁故障前后的磁场强度B与永磁体材料的性能参数Hc(永磁材料的矫顽力)和Br(剩余磁感应强度)的关系:

(20)

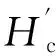
(21)

由式(19)和式(21)可得，在使用Ansoft软件仿真分析过程中，建立永磁同步电机的匝间短路和永磁体退磁的单一故障模型只需分别改变绕组的匝数和永磁体的矫顽力；而建立耦合故障模型则需同时改变两者的值，通过控制数值的大小分别建立故障程度为20%、40%、60%和80%的耦合故障模型。

2.2 耦合故障仿真及分析

对图1(b)表示的电机1/4模型，分别在空载和额定负载工况下进行不同耦合故障程度的瞬态磁场分析，得到电磁场分布云图和相关特征参数曲线图，并将不同条件下的结果进行对比。

二维电磁场分布仿真结果主要包括磁感线分布云图、磁密分布云图和磁密矢量分布云图等，由于不同云图在不同故障程度下反映的结果相似，因此只需选择其中一种作具体分析，将不同工况下不同故障程度的磁感线分布云图作对比分析，如图2所示。

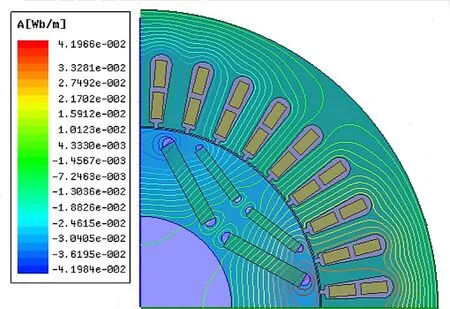
(a) 无故障空载工况

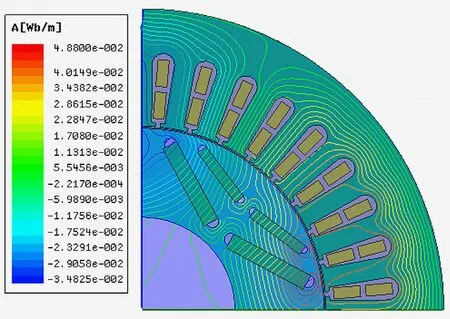
(b) 无故障额定负载工况

(c) 20%故障空载工况

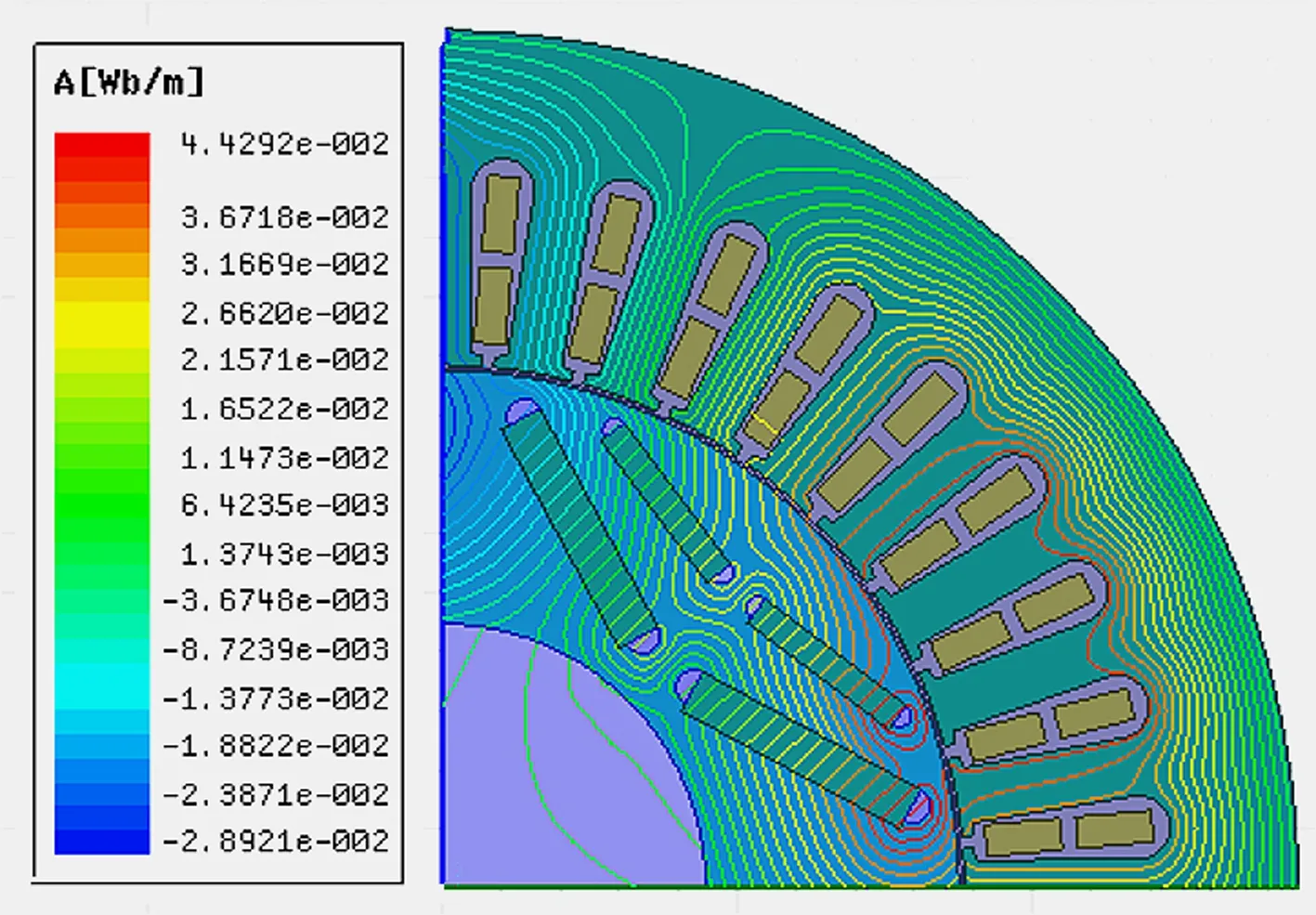
(d) 20%故障额定负载工况

(e) 40%故障空载工况

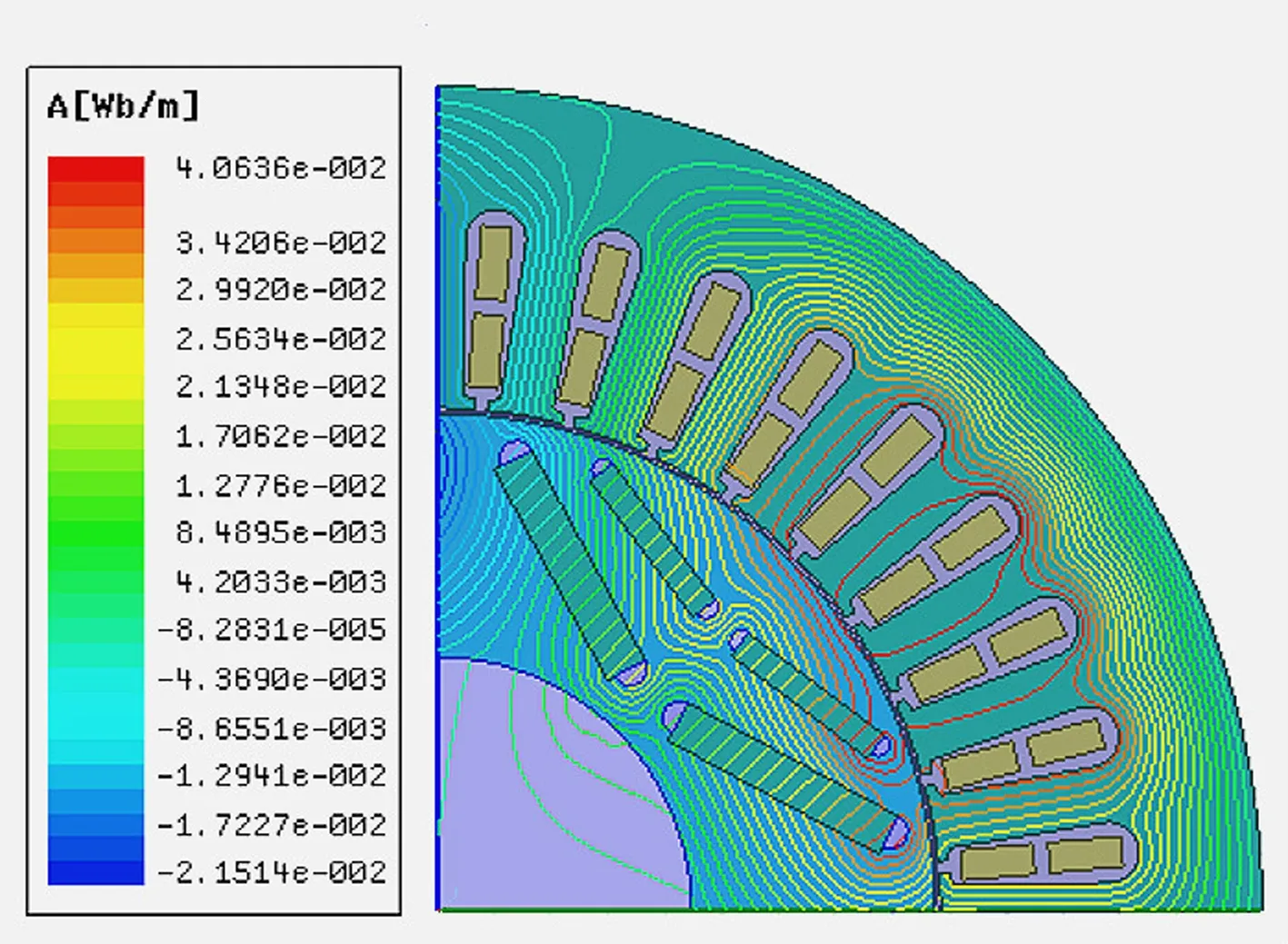
(f) 40%故障额定负载工况

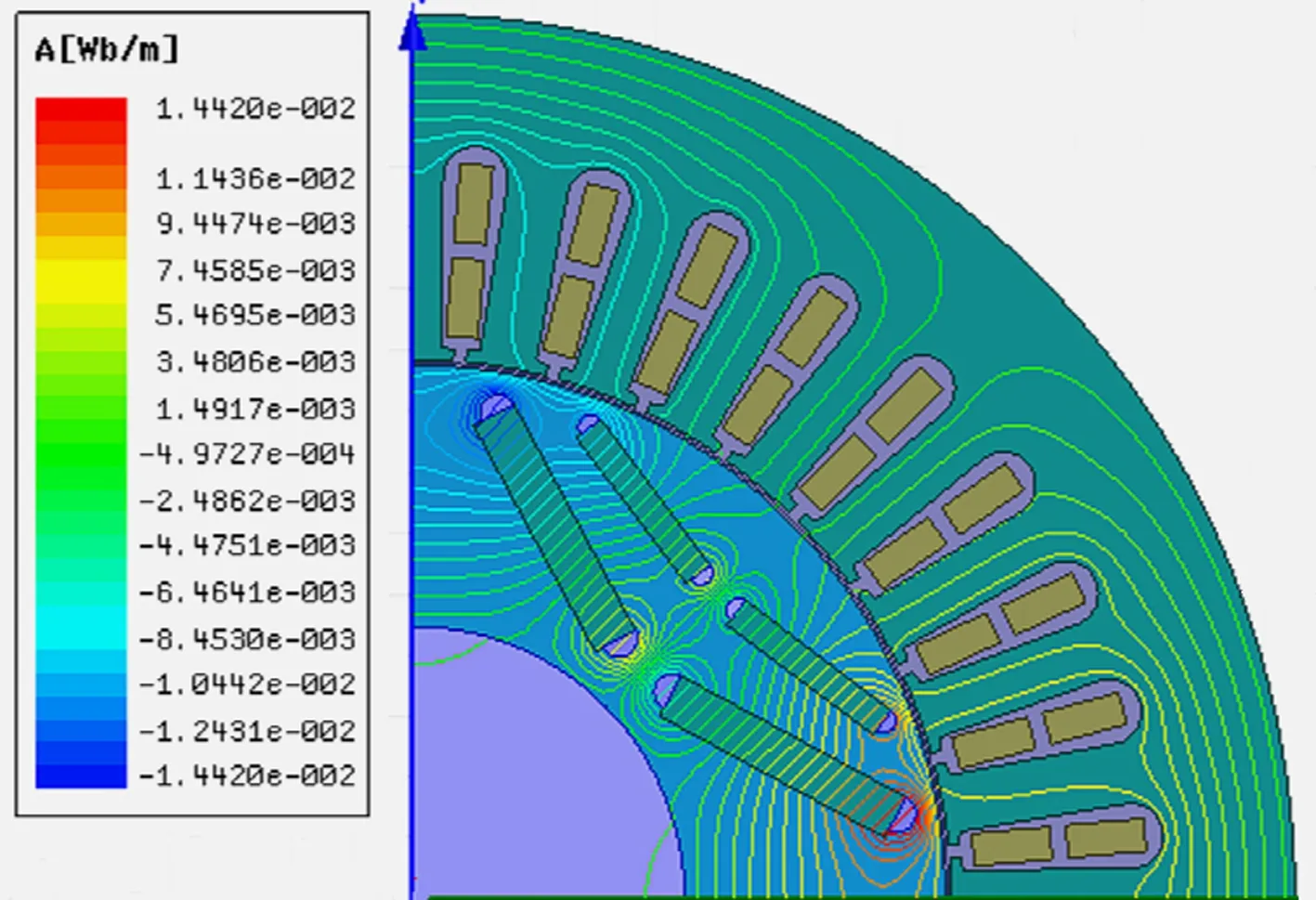
(g) 60%故障空载工况

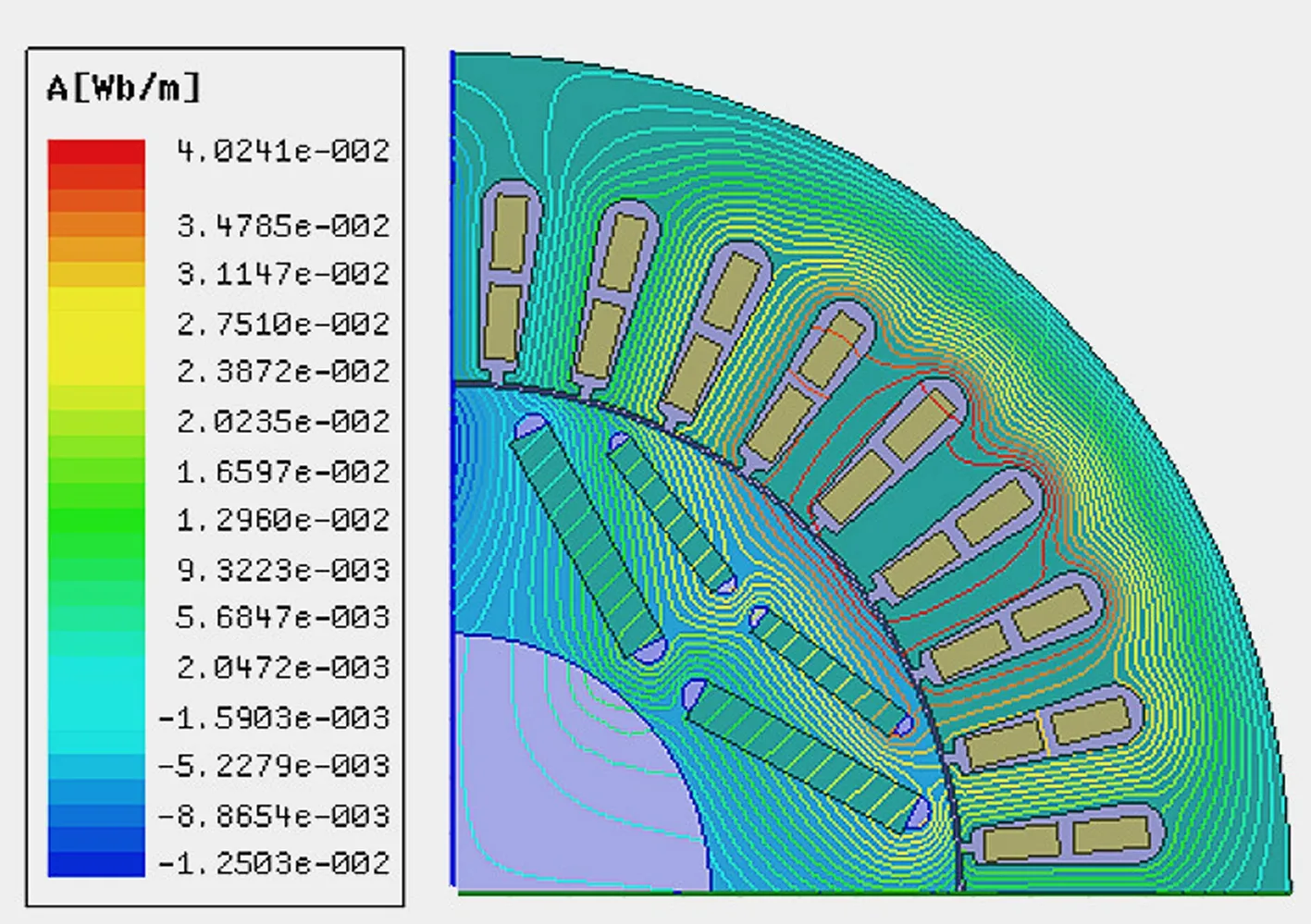
(h) 60%故障额定负载工况

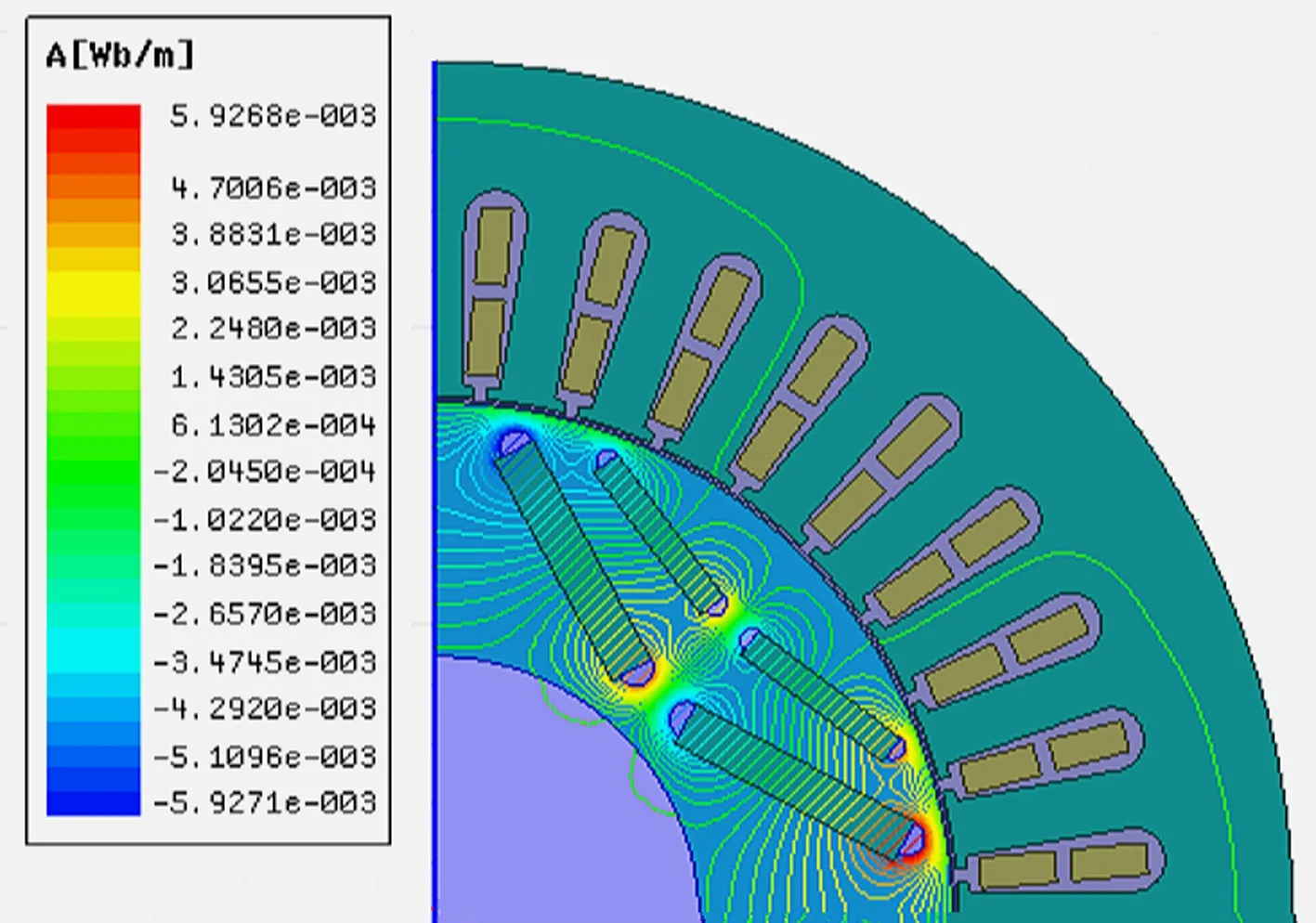
(i) 80%故障空载工况

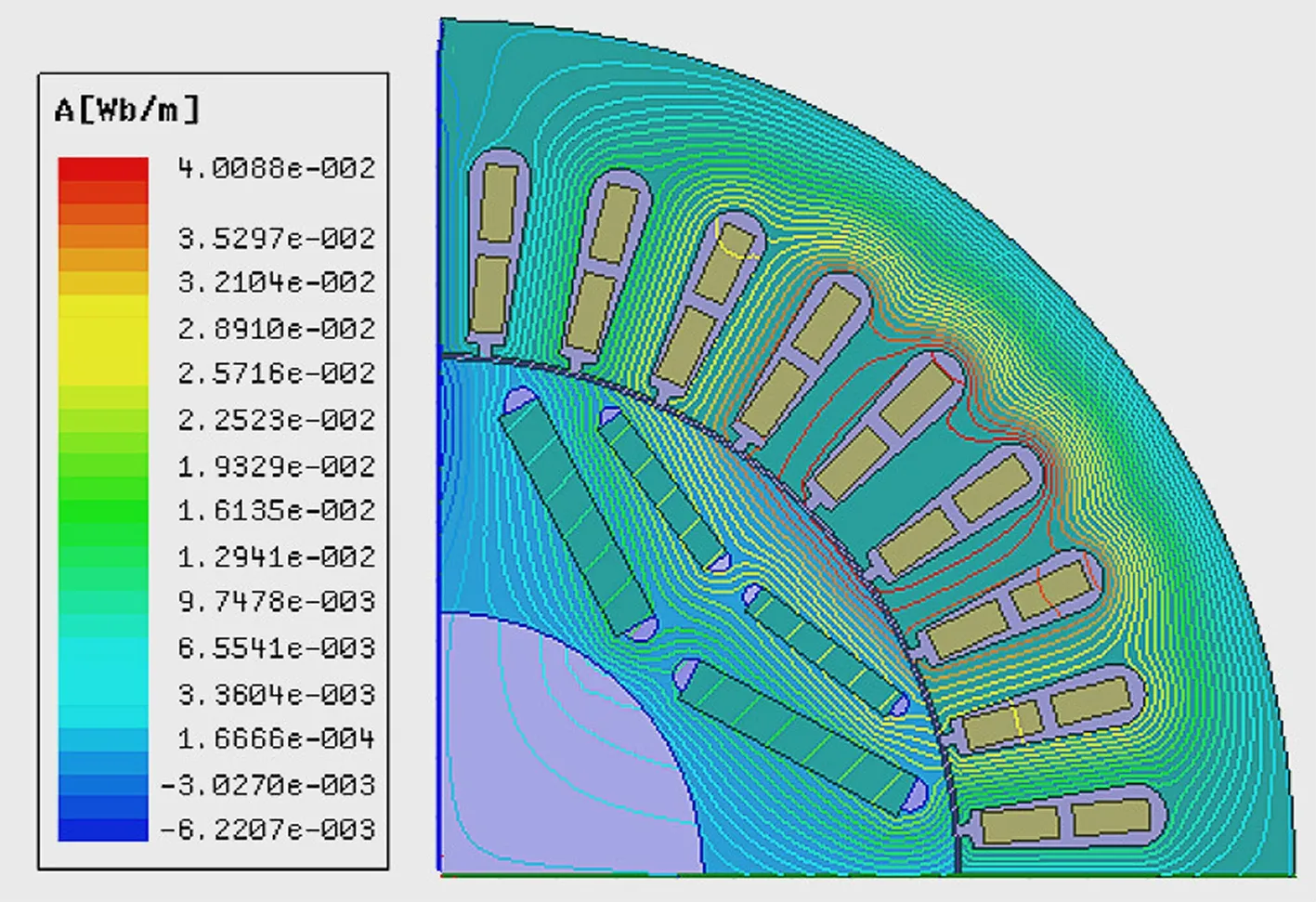
(j) 80%故障额定负载工况

由图2中空载和额定负载两种不同工况对比可知，空载工况下，随着故障程度的增加，磁感线变稀疏，数量明显减少，数值也减小；额定负载工况下，磁感线数量看似变密集，实际上数值减小。因此，该耦合故障会引起电机电磁场的畸变，导致电磁场强度减小。

电机相关特征参数包括转矩、相反电动势、电流、转速和转子位置等，根据前面对永磁同步电机重要性能参数的计算分析以及该耦合故障的故障机理可知，转矩和相反电动势为典型特征参数，因而选择对其曲线变化特点进行对比分析。

1) 转矩曲线变化特点分析

不同工况下的转矩变化曲线如图3所示。为深入分析图3(a)中曲线的变化特点，将其中一段时间内的曲线放大(见图3(b))。由图3可以看出，电机电磁转矩的变化特点是，随故障程度的增加，转矩的幅值均减小；空载工况下的周期变化不明显，额定负载工况下周期明显变大。

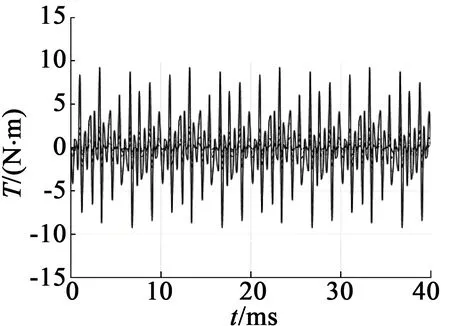
(a) 空载

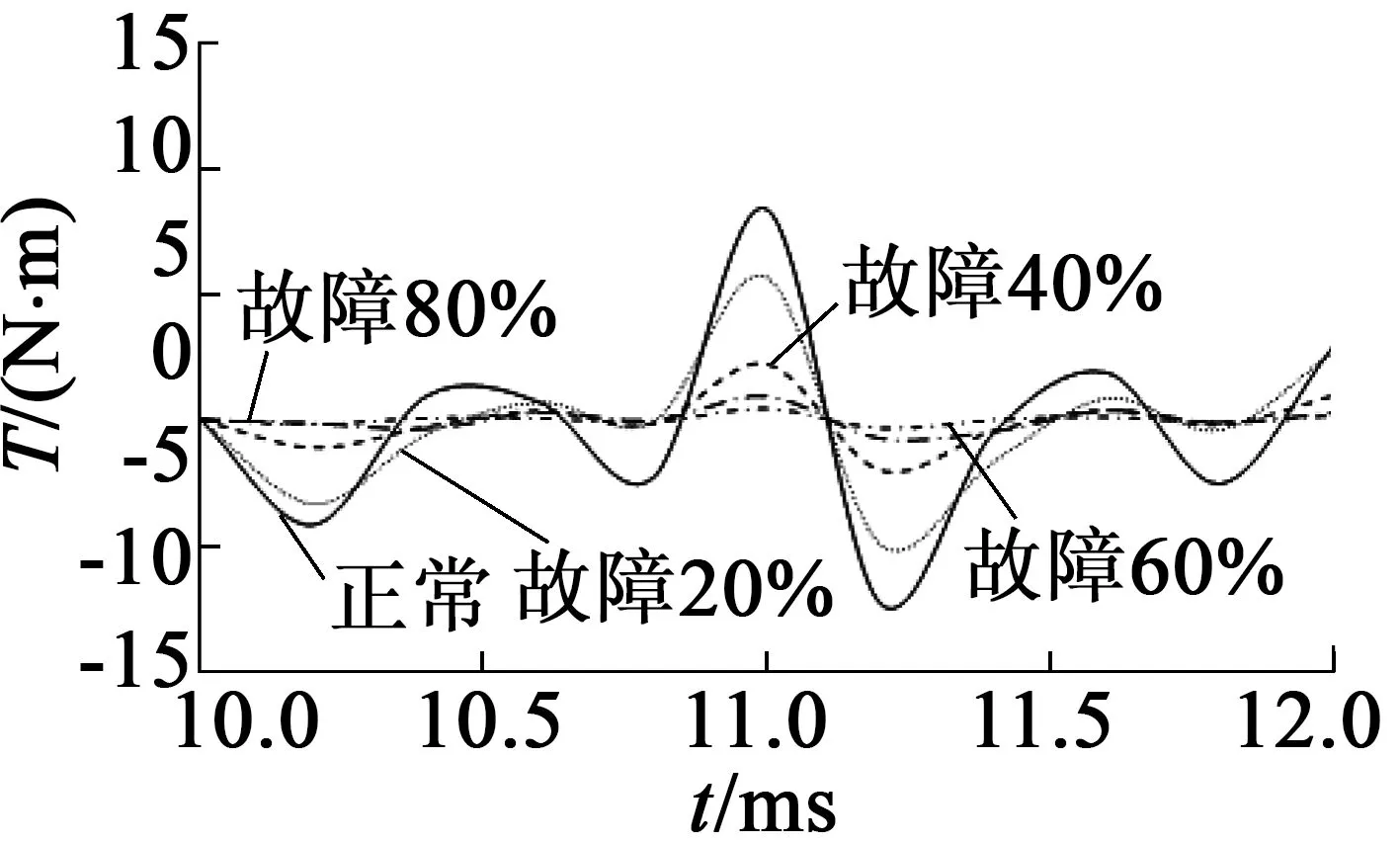
(b) 空载局部放大

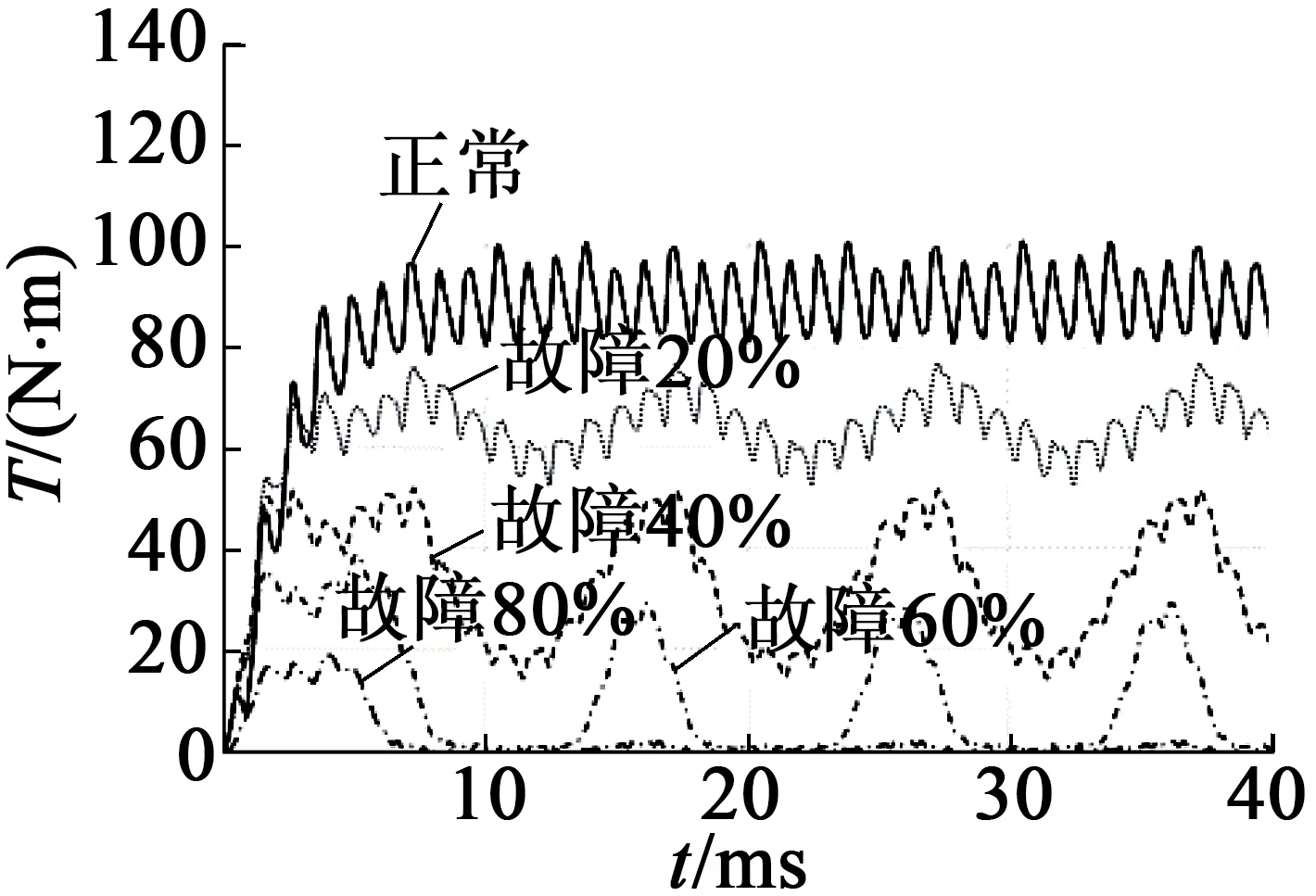
(c) 额定负载

图3不同工况下转矩曲线图

2)相反电动势曲线变化特点分析

如图4所示，电机A相反电动势的变化特点是，随故障程度的增加，幅值均减小；空载工况下的周期变化不明显，额定负载工况下周期有轻微变化。

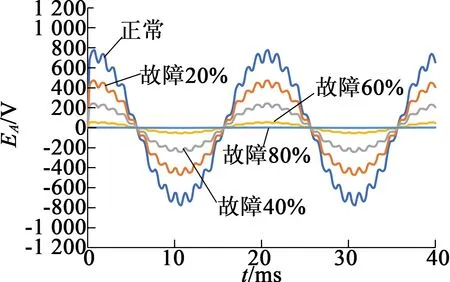
(a) 空载

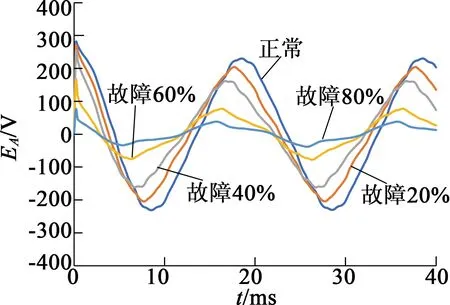
(b) 空载局部放大

图4不同工况下A相反电动势曲线图

2.3 相反电动势谐波含量分析

前面对电磁场分布和特征参数曲线的分析及仿真结果，仅给出了定性的变化趋势。为进一步深入揭示永磁同步电机耦合故障的特性，利用傅里叶变换，分别分析不同工况以及不同故障程度下的相反电动势谐波含量，如表2、表3所示(表中谐波含量是谐波与基波的比值，谐波次数是谐波频率与基波频率的比值，基波频率是50 Hz)。

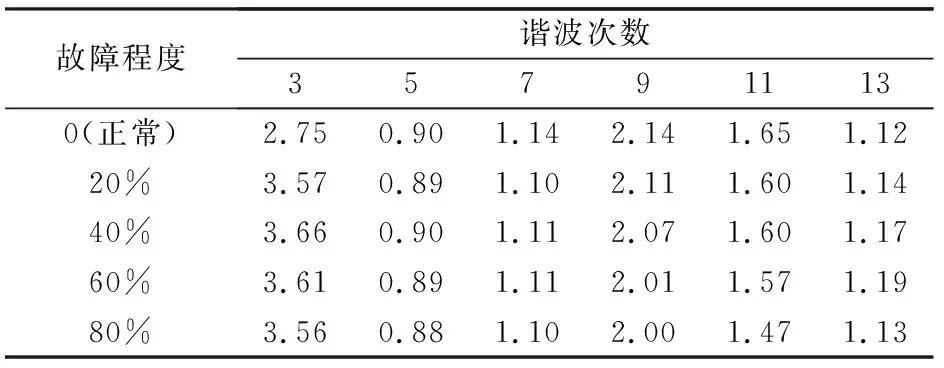
表2 空载工况下A相反电动势谐波含量(单位：%)

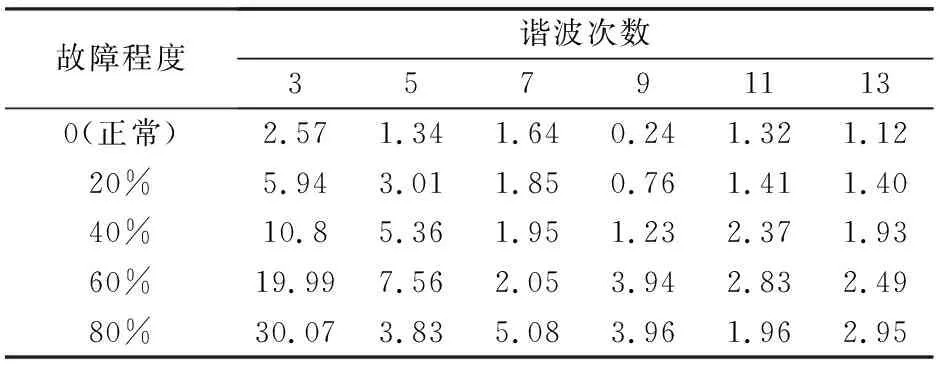
表3 额定负载工况下A相反电动势谐波含量(单位：%)

由表2可知，空载工况下A相绕组反电动势三次谐波含量呈小幅度增加趋势，其它次数的谐波含量只有轻微改变，可忽略不计。

由表3可知，额定负载工况下A相绕组反电动势三次谐波含量呈明显增加趋势，而其它次数的谐波含量虽有所增加，但相对于三次谐波来说可忽略。

综合表2、表3可知，两种不同工况下只有三次谐波含量变化最为明显，其它次谐波含量较三次谐波含量而言，虽有变化但幅值较小，为此，特选择三次谐波含量作为永磁同步电机匝间短路和永磁体退磁耦合故障的特征量，用以表征永磁同步电机是否存在对应耦合故障的判定依据。以此为基础，额定工况下还可根据其增加量的大小进一步判断电机的故障程度，如表4所示(表中的值为近似值，即在该数值左右即可)。

表4 三次谐波含量的增加量与故障程度的关系

3 数学模型验证

3.1 永磁同步电机数学模型

永磁同步电机在三相坐标系下的数学模型[16]：

(22)

式中:ua,ub,uc分别为三相绕组电压；ia,ib,ic分别为三相定子电流；Rs为定子绕组的电阻；φa,φb,φc分别为三相定子磁链；p为时间t的微分算子。

(23)

式中:

(24)

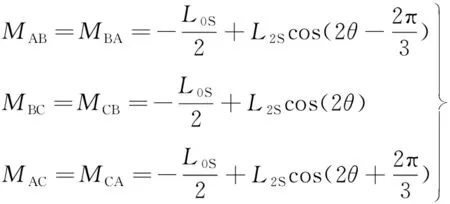
(25)

式中:LAA,LBB,LCC分别为定子绕组的自感；Mxx分别为定子绕组之间的互感；φf为永磁体交链于定子相绕组磁链的幅值；θ为转角；L0S为主自感的恒定分量；L2S为主自感的倍频分量。

3.2 数学模型解析

由仿真分析结果可将A相反电动势作为判断该耦合故障的特征量，因此通过数学模型求解验证A相反电动势的仿真曲线是否正确。

由于三相对称，故三相电流大小相等，相位相差120°。将式(24)、式(25)代入式(23)可得:

将式(26)代入式(22)可得:

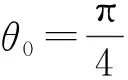
将式(18)代入式(27)得:

3.3 解析结果分析

由图4可知，不同工况下的A相反电动势曲线与正弦三角函数曲线(空载工况下的不平滑曲线是由于电机内部结构所致)非常相似，根据三角函数特性，式(28)可简化成正弦函数曲线，这表明仿真得到的正常条件下的曲线趋势和数学模型解析得到的曲线趋势十分吻合。

将空载和负载工况下的φf分别代入式(28)中，可得到两种不同工况下的A相电压幅值分别为807.53 V和278.63 V。通过计算得到的幅值和仿真幅值相近。由于数学模型经过简化，数值上有差距属于正常范围内。这表明前面建立的永磁同步电机二维物理模型是正确的，这为耦合故障仿真分析奠定了基础。

4 结 语

耦合故障对永磁同步电机的电磁场分布和特征参数曲线都有明显影响。电机出现耦合故障后电磁场强度减小，特征参数的幅值减小，周期也相应变化。

耦合故障对空载工况的电磁场分布影响明显,随着故障程度增加，空载工况下的磁感线数量减少明显，且数值减小量也比额定负载多;耦合故障对额定负载的特征参数影响较大,随着故障程度的增加，不同工况下各特征参数的幅值均减小，但额定负载工况下周期变化明显。

三次谐波含量增加可作为判断耦合故障的依据。在额定工况下，三次谐波含量的增加量可判断电机的故障程度，即增加量越大，故障程度越重。