“圆”专题复习

张杭嫣

圆，是几何图形中最完美的图形，也是初中几何中不多见的曲线图形.在这一章中，知识点众多，很多同学学得较为吃力.本文通过一组例题来为大家梳理本章知识点，构建知识网络.

知识点一：圆中的角——圆周角和圆心角

圆周角和圆心角是圆中两类特殊的角，根据“同弧所对的圆周角是圆心角的一半”这条定理，可以将这两类角进行互相转换.

例1△ABC为⊙O的内接三角形，若∠AOC=160°，则∠ABC的度数是（ ）.

A.80° B.160°

C.100° D.80°或100°

【分析】首先根据题意画出图形.如图1，画图时要特别注意，△ABC可能为锐角三角形，也可能为钝角三角形，因此要对点B在优弧和劣弧上两种情况加以分析，由圆周角定理即可求得∠ABC的度数，再根据圆的内接四边形的性质，可求得∠AB′C的度数.

解：如图1，∵∠AOC=160°，

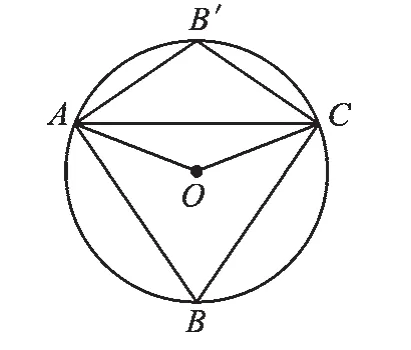
图1

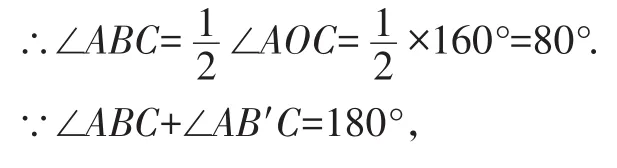
∴∠AB′C=180°-∠ABC=180°-80°=100°.

∴∠ABC的度数是：80°或100°.

故选：D.

【点评】看到圆中的角，我们往往要根据图形先分析：这是圆周角，还是圆心角？利用哪条弧可以进行转化？同时在没有图形或点在圆周上运动时，我们也要进一步思考：答案是不是唯一的？有没有不同于此时的情况？要注意数形结合与分类讨论思想的应用，注意别漏解.

例2 如图2，AB是⊙O的直径，C、D是⊙O上的两点，分别连接AC，BC，CD，OD.若∠DOB=140°，则∠ACD=（ ）.

图2

A.20° B.30° C.40° D.70°

【分析】根据条件“AB是⊙O的直径”，我们能轻松得到∠ACB=90°，再根据圆周角定理，由∠DOB求出∠DCB的度数，从而求解.

解：∵AB是⊙O的直径，

∴∠ACB=90°，

∵∠DOB=140°，

∴∠DCB=70°，

∴∠ACD=∠ACB-∠DCB=20°.

故选：A.

【点评】圆中我们可以常见到两类特殊三角形：当出现两条相等的半径时，我们就找到了等腰三角形；当出现直径时，我们利用“直径所对的圆周角是直角”，就可以找到直角三角形.

知识点二：圆中的弦——垂径定理

例3如图3，AD是⊙O的直径，弦BC⊥AD于E，AB=BC=12，则OC= .

图3

【分析】根据条件弦BC⊥AD，我们找到了垂径定理的条件，求得BC=6，进一步在Rt△ABE中，求出特殊角度30°，再将30°角转化到Rt△COE中，从而求解OC的长度.

∵AB=12，

∴Rt△ABE中，∠A=30°，

∴∠COE=2∠A=60°，

∴Rt△COE中，OE=2 3 ，OC=4 3.

【点评】垂径定理结论中的“平分”既能产生边的结论，又能通过弧产生角的结论，结合垂径定理中的直角，是一个很好的基础模型.

例4如图4，⊙O直径AB和弦CD相交于点E，AE=2，EB=6，∠DEB=30°，求弦CD的长.

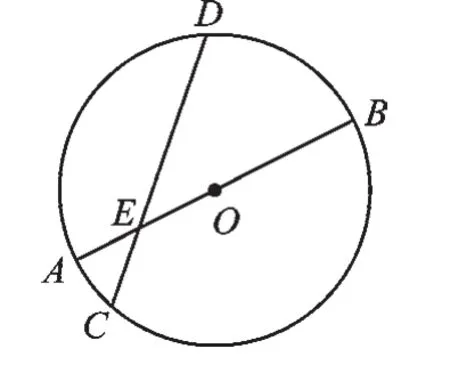
图4

【分析】过O作OF垂直于CD，连接OD，利用垂径定理得到F为CD的中点，由AE+EB求出直径AB的长，进而确定出半径OA与OD的长，由OA-AE求出OE的长，在直角三角形OEF中，利用30°角所对的直角边等于斜边的一半求出OF的长，在直角三角形ODF中，利用勾股定理求出DF的长，由CD=2DF即可求出CD的长.

解：过点O作OF⊥CD，OF交CD于点F，连接OD，如图5.

图5

在Rt△OFD中，OF=1，OD=4，

根据勾股定理得：

【点评】圆中已知弦，要求弦长的问题，我们可以尝试用构造垂径定理的直角三角形来解决，而本题中的30°角又提供了一个更特殊的直角三角形，进而可以综合解题.

知识点三：圆中的线——切线

例5如图6，AC是⊙O的直径，PB切⊙O于点D，交AC的延长线于点B，且∠DAB=∠B.

∴F为CD的中点，即CF=DF，∵AE=2，EB=6，

∴AB=AE+EB=2+6=8，

∴OA=4，∴OE=OA-AE=4-2=2，

在Rt△OEF中，∠DEB=30°，

图6

（1）求∠B的度数；

（2）若BD=9，求BC的长.

【分析】由PB为圆的切线，利用切线性质，得到PB与OD垂直，在△ODB中，利用三角形的内角和定理即可求出∠B的度数，进一步可求出线段BC的长.

解：（1）连接OD.

∵PB切⊙O于点D，∴OD⊥PB

∵OA=OD，

∴∠COD=2∠A，而∠A=∠B，

∴∠COD=2∠B，

∴在Rt△BOD中，∠B=30°.

（2）∵在Rt△BOD中，BD=9，

【点评】切线是圆中过圆上一点的一条特殊的线，“见切线，找半径，得垂直”，因此，利用切线，我们可以轻松地找到直角三角形，进一步结合勾股定理等综合解题.

例6如图7，以△ABC的BC边上一点O为圆心作⊙O，⊙O经过A，C两点且与BC边交于点E，点D为CE的下半圆弧的中点，连接AD交线段EO于点F，若AB=BF.

图7

（1）求证：AB是⊙O的切线；

【分析】求证圆的切线，在直线与圆有公共点时即转化为求证直角，从而产生辅助线AO；证出的直角又为求解（2）中的sinB提供了条件，（2）中突破点为“点D为CE的下半圆弧的中点”，从而产生Rt△DOF.

证明：（1）连接OA，OD.

∵点D为CE的下半圆弧的中点，

∴OD⊥BC，∴∠EOD=90°，

∵AB=BF，OA=OD，

∴∠BAF=∠BFA，∠OAD=∠D，

而∠BFA=∠OFD，

∴∠OAD+∠BAF=∠D+∠OFD=90°，

即∠OAB=90°，∴OA⊥AB，

∴AB是⊙O切线.

解：（2）OF=CF-OC=4-r，OD=r，DF=，

在Rt△DOF中，OD2+OF2=DF2，

解得r1=3，r2=1（舍去），∴半径r=3，

∴ OA=3，OF=CF-OC=4-3=1，BO=BF+FO=AB+1.

在Rt△AOB中，AB2+OA2=OB2，

∴AB2+32=（AB+1）2，

【点评】求证切线时，我们要判断这条直线与圆有无公共点，有公共点时，我们“找半径，证垂直”，无公共点时，我们“作垂直，证半径”.要学会运用切线产生的直角三角形进行综合解题.

知识点四：内切圆与外接圆

例7在△ABC中，∠A=50°，

（1）若点O是△ABC的外心，则∠BOC=__.

（2）若点O是△ABC的内心，则∠BOC=__.

【分析】从定义入手，我们可以得到，外心是三角形三边垂直平分线的交点，进而根据圆周角定理求解；而内心是三角形三个内角角平分线的交点，从而根据角平分线及三角形内角和定理综合解题.

解：（1）∵点O是△ABC的外心，

∴∠BOC=2∠A=100°.

图8

（2）∵△ABC中，∠A=50°.

∴∠BOC=180°-65°=115°.

【点评】此题考查了内心、外心两个基本定义，我们要根据题意画出符合题意的草图，抓住定义，综合运用圆周角、三角形内角和等知识解题.

例8如图10，在△ABC中，AB=AC，⊙O是△ABC的内切圆，它与AB，BC，CA分别相切于点D，E，F.

图9

∴∠ABC+∠ACB=180°-50°=130°，

∵点O是△ABC的内心，

∴OB、OC分别平分∠ABC、∠ACB，

图10

（1）求证：BE=CE；

（2）若∠A=90°，AB=AC=2，求⊙O的半径.

【分析】（1）根据条件“⊙O是△ABC的内切圆”，我们可以利用切线长定理，证得BE=CE；（2）若∠A=90°，再加上切线产生的两个直角，我们可以证得四边形ODAF是矩形，进一步证得四边形ODAF是正方形，从而求解.

证明：（1）∵⊙O是△ABC的内切圆，切点为D，E，F，见图11.

图11

∴AD=AF，BD=BE，CE=CF，

∵AB=AC，∴AB-AD=AC-AF，

即BD=CF，∴BE=CE.

解：（2）连接OD，OF.

∵⊙O是△ABC的内切圆，切点为D，E，F，

∴∠ODA=∠OFA=∠A=90°，

∴四边形ODAF是矩形，

又∵OD=OF，∴四边形ODAF是正方形.

设OD=AD=AF=r，则BE=BD=CF=CE=2-r.

在△ABC中，∠A=90°，

又∵BC=BE+CE，

【点评】在出现内切圆条件时，我们既可以直接使用切线的性质，又可以组合两条切线，使用切线长定理，还可以使用内心等结论，因此，要根据题目要求灵活运用.

例9图12是一块△ABC余料，已知AB=20cm，BC=7cm，AC=15cm，现将余料裁剪成一个圆形材料，则该圆的最大面积是_________.

图12

【分析】当该圆为三角形内切圆时面积最大.设内切圆半径为r，则该三角形面积可表示为：·r·（AB+BC+AC）=21r.若作BC边上的高AD，三角形的面积公式可表示为·BC·AD，利用勾股定理可得AD，易得三角形ABC的面积，从而可得r，求得圆的面积.

解：如图13所示，

图13

图14

过点A作AD⊥BC交BC的延长线于点D，如图 14，设 CD=x，在Rt△ABD中，由勾股定理得：

AD2=AB2-BD2=400-（7+x）2，

在Rt△ACD中，AD2=AC2-x2=225-x2，

∴400-（7+x）2=225-x2，

解得：x=9，∴AD=12，

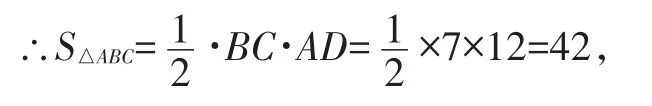
∴21r=42，∴r=2.

∴该圆的最大面积为：

S=πr2=π·22=4π（cm2）.

【点评】本题中我们把内切圆与面积进行结合，通过内切圆构造出3个垂直，进一步构造高线，用面积法列出了基本算式.用面积来求内切圆半径也是一个基本方法.

知识点五：弧长与扇形面积

例10 现有一张圆心角为108°，半径为40cm的扇形纸片，小红剪去圆心角为θ的部分扇形纸片后，将剩下的纸片制作成一个底面半径为10cm的圆锥形纸帽（接缝处不重叠），则剪去的扇形纸片的圆心角θ为

图15

【分析】已知圆锥形纸帽底面半径是10cm，则展开图扇形的弧长是20πcm.根据弧长公式l=nπr÷180，就可以知道剪后的扇形圆心角度数，从而求出θ.

解得：n=90°.

∵原始扇形彩纸片的圆心角是108°，

∴剪去的扇形纸片的圆心角为108°-90°=18°.故答案为：18°.

【点评】本题综合考查扇形和圆锥的相关计算.解题思路：（1）圆锥的母线长等于侧面展开图的扇形半径；（2）圆锥的底面周长等于侧面展开图的扇形弧长.正确对这两个关系进行记忆是解题的关键.

例11如图，在矩形ABCD中，已知AB=4，BC=3，矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置，再绕右下角的顶点继续向右旋转90°至图②位置……以此类推，这样连续旋转2015次后，顶点A在整个旋转过程中所经过的路程之和是（ ）.

图16

A.2015π B.3019.5π

C.3018π D.3024π

【分析】首先求得每一次转动的路线的长，发现每4次一循环，找到规律然后计算即可.

解：转动一次，A的路线长是：2π；转动第二次，A的路线长是：转动第三次，A的路线长是：；转动第四次，A的路线长是：0；转动第五次，A的路线长是：

以此类推，每4次一循环，故顶点A转动4次经过的路线长为：4=503余3，顶点A转动2015次经过的路线长为：6π×504=3024π.故选：D.

【点评】本题主要考查了弧长公式的运用和探索规律问题.第一步，列举出前面若干次的计算结果；第二步，寻找出循环的周期或前n次呈现的规律；第三步，归纳，根据周期或规律寻找题目答案.其中，发现规律是解决问题的关键.