学好“圆”的几个抓手

周进荣

与三角形、四边形一样，圆是“空间与图形”的主要研究对象，也是基本的平面图形.本章在基本的直线形——三角形、四边形等基础上，进一步研究一个基本的曲线形——圆，它有很多新的知识点，这些知识点与前面的知识是紧密联系的.因此，同学们在解题时需结合直线形中的定理、法则，先由条件对图形有比较好的“认识”，再结合已有的经验，联想相关知识，分析隐含条件，将问题化解为若干小问题，逐一解决.

一、知识考点

考点课标要求知识与技能目标掌握应用圆圆及其相关概念弧、弦、圆心角的关系，点与圆、直线与圆的位置关系圆周角和圆心角的关系，直径所对圆周角的特征三角形的内心和外心，正多边形概念及正多边形与圆的关系切线的概念，探索切线与过切点的半径的关系会判定圆的切线，会过圆上一点画圆的切线，垂径定理计算弧长和扇形的面积，会计算圆锥的侧面积和表面积了解 √ √ √ √理解 √√ √

二、几个抓手

1.抓住两个角.

圆心角、圆周角犹如圆中的一对“双胞胎”，形影不离，且同弧或等弧所对的圆周角是圆心角度数的一半.

例1 如图1，已知⊙O的直径为8cm，A、B、C三点在⊙O上，且∠ACB=30°，则AB长为（ ）.角，它等于所对的圆心角度数的，所以

图1

【分析】如图2，∠ACB是所对的圆周连接AO、BO，则∠AOB=60°，又因为AO、BO是半径，可得△AOB为等边三角形.

【解答】如图2，连接AO、BO.

图2

故选：B.

【点评】在圆中，圆周角的度数等于它所对弧上的圆心角度数的一半，同弧或等弧所对的圆周角相等，此外，圆内接四边形的对角互补（或圆内接四边形的外角等于和它相邻内角的对角）.

2.抓住两个垂直.

圆中有两个隐性垂直：直径所对的圆周角为直角；切线垂直于半径.挖掘这两种垂直关系，可以有效地把许多问题转化到直角三角形中，使问题得以解决.

例2 如图3，已知在⊙O中，AB是⊙O的直径，AC=8，BC=6.则⊙O的面积为 .

∵∠ACB=30°，

∴∠AOB=60°.

又∵AO=BO，

∴△AOB为等边三角形.

图3

【分析】如图3，要求⊙O的面积，只要求出⊙O的半径即可.由AB是⊙O的直径，可知∠ACB=90°，再根据勾股定理，可求出直径AB的长，从而求得⊙O的面积.

【解答】∵AB是⊙O的直径，

∴∠ACB=90°，

又∵AC=8，BC=6.

∴⊙O的半径为5，

则⊙O的面积为：π×52=25π.

【点评】圆中的直径与90°的圆周角是紧密联系在一起的.若有直径，则要想到直径所对的圆周角是直角；若有90°的圆周角，往往需要作出90°的圆周角所对的弦（即直径）.

3.抓住两种关系.

点与圆的位置关系、直线与圆的位置关系是圆中常见的两种位置关系，特别是当直线和圆相切时，要重点掌握切线的判定和性质定理.

例3 如图4，⊙O的半径为3cm，B为⊙O外一点，OB交⊙O于点A，AB=OA.动点P从点A出发，以πcm/s的速度在⊙O上按逆时针方向运动，运动一周回到点A立即停止.当BP与⊙O相切时，点P运动的时间为（ ）.

A.1s B.3s

C.5s D.1s或5s

图4

【分析】要求点P运动的时间，必须找出点P所在的位置.当BP与⊙O相切时，如图5情形.考虑到运动的全过程，当点P运动到点P关于OB的对称点P′位置时，BP′与⊙O也相切，因此要考虑两种情形.

图5

【解答】如图5，连接OP，若BP与⊙O相切，则∠OPB=90°.

由AB=OA可知，

所以∠B=30°，∠BOP=60°.

此外，考虑到运动的全过程，显然，当点P运动到关于OB的对称点P′位置时，BP′与⊙O也相切.

∴点P运动到P′位置需要5s.

综上，点P运动的时间为1s或5s.

故选：D.

【点评】当直线和圆相切时，切线垂直于经过切点的半径，此时往往需要连接切点和圆心，得到圆的半径，再去解直角三角形.另外，过圆外一点画圆的切线，一般有两条.

4.抓住两大定理.

圆中的计算“丰富多彩”，有关于线段、角的计算，扇形及阴影面积的计算以及圆柱、圆锥侧面展开图的计算，在实际问题中往往要用到垂径定理和勾股定理.

例4如图6，AC是⊙O的直径，弦BD⊥AO于E，连接BC，过点O作OF⊥BC于F，若BD=8cm，AE=2cm，则OF的长度为（ ）.

图6

【分析】如图6，因为OF⊥BC于F，根据垂径定理，可知F是BC的中点，又因为点O是AC的中点，所以OF是△ABC的中位线，则OF的长度等于AB的长度的

【解答】如图7，连接AB.

图7

又∵AE=2cm，

故选：D.

【点评】垂径定理是圆中最重要的一个定理，它将线段的位置关系转化为数量关系，另外，圆中常常添加与垂径定理相关的辅助线、与切线有关的辅助线，这些都构成了直角三角形这个基本图形，所以勾股定理的运用在问题的解决中往往发挥不可替代的作用.

5.抓住两个特征.

在平面几何中，同学们常常想到的是构造直线形辅助线转化条件，从而利用三角形、四边形的知识解决问题，但这样的话，辅助线的添加就局限在了直线形，实际上曲线形辅助线在一些特定条件下，更有利于条件集中.辅助圆是曲线形辅助线的代表，利用辅助圆，会让图形的条件更丰富.

那什么时候需构造辅助圆？怎样构造辅助圆？需要抓住题目中两个显著的特征.

例5如图8，在四边形ABCD中，AB=AC=AD，∠BAC=26°，∠CAD=74°，则∠BDC=______°，∠DBC=_____°.

图8

又∵OF⊥BC于F，

根据垂径定理，知F是BC的中点，

又∵点O是AC的中点，

∴OF是△ABC的中位线，

【分析】如图8，在四边形ABCD中，AB=AC=AD，B、C、D三点到点A的距离相等，所以B、C、D三点共圆，因此想到构造辅助圆⊙A.

【解答】如图9，以A为圆心，AB为半径画37°.

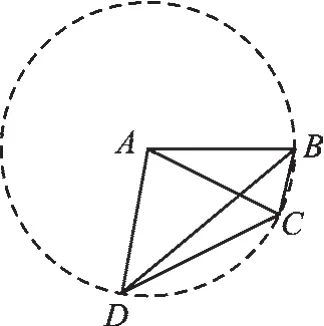
图9

【点评】当遇有公共端点的等线段长时，通常以公共端点为圆心，等线段长为半径构造辅助圆，再利用圆周角和圆心角的关系解题.

例6如图10，在Rt△ABC中，AB⊥BC，AB=6，BC=4，P是△ABC内部的一动点，且满足∠PAB=∠PBC.则线段CP长的最小值为（ ）.

图10

【分析】如图10，在Rt△ABC中，AB⊥BC，所以∠ABC=90°，所以∠ABP+∠PBC=90°，又因为∠PAB=∠PBC，所以∠PAB+∠ABP=90°，则∠P=90°，所以动点P在以AB为直径的圆上，且在△ABC内部，如图11所示.

图11

【解答】如图12，以AB为直径画⊙O，连接OC交⊙O于点P′，当点P在OC上的P′位置时，CP长最小，此时CP=CP′=OC-OP′=

故选：B.

图12

【点评】在动点问题中，当动点所在顶点的角是90°时，利用90°的圆周角所对的弦是直径，可以以斜边为直径构造辅助圆，像这样的辅助圆在研究几何最值问题时具有举足轻重的作用.如果将题目中“P是△ABC内部的一动点”改为“P是平面内一动点”，而其余条件不变，我们还能求出线段CP长的最大值.同学们不妨动笔算算看.