基于函数单调性的数学概念教学

☉浙江省台州市台州第一中学 汪正旺

任何数学理论与数学框架的学习与构建都必须建立在一定的基础之上，数学概念正是充当这一角色的重要内容，高中数学的抽象性之强要求教师在课堂教学中必须注重生产生活事例的引入与分析，学生在充分建立感性认识的基础上才能将高度抽象与概括的数学概念领悟透彻.函数的单调性这一高中阶段的首个数学语言是研究指数函数、对数函数等其他函数的重要基础，函数的值域、定义域、比较两数大小、不等式等多个具体问题的研究都离不开单调性这一最为基本的函数知识，笔者结合这一概念的实际教学对高中数学概念教学浅要谈谈自己的一点想法.

一、创设情境，引入课题

问题1：观察以下函数，作图并指出其变化趋势.

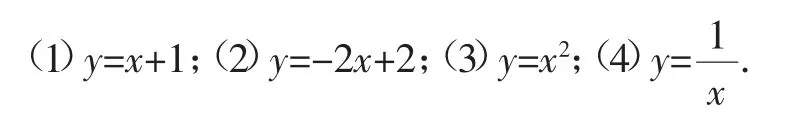
（过程略）

问题2：你能对“图像呈逐渐上升趋势”的意思进行准确的描述吗？x与函数值y此时是怎样相互影响的呢？

生：x增大，y随之增大，所以它的图像呈上升趋势；x增大，y减小，所以它的图像呈下降趋势.

师：很好，这就是函数的单调性，一个非常重要的性质，也是我们今天研究的主题.

函数的单调性这一内容的教学，教师应首先要求学生能够在实际问题的研究中学会建模，要求学生在掌握建模过程与方法的基础上充分体会其重要意义与价值，使学生学会运用函数思想来解决实际问题并因此获得思维能力的提升.因此，教师在进行这一概念的教学之前首先应该对学生的认知发展水平与已有的知识经验进行摸底与分析，并在此基础上引导学生展开观察、猜想与归纳，引导学生在函数图像的观察与分析中学会应用函数知识来解题，使学生充分体会函数知识的应用价值并建立数学与生活息息相关的认知.

二、抽象概括，形成概念

思考并讨论：

（1）若某函数在区间（0，+∞）上有x=1时y=1，x=2时y=3，则是否可以说在该区间上y随着x的增大而增大呢？

（2）若x=1，2，3，4时，对应地y=1，3，4，6，则是否可以说在区间（0，+∞）上y随着x的增大而增大呢？

（3）若有n个正数x1＜x2＜x3＜…＜xn，它们对应的函数值满足y1＜y2＜y3＜…＜yn，则是否可以说在区间（0，+∞）上y随着x的增大而增大呢？

生：不能，我来举例说明（略）.

问题3：如果某函数是增函数，你能对其进行数学语言的表述吗？你是否能够尝试给出确切的定义？请运用自己的语言进行表达并讲给小组成员听，各小组进行一定的交流并形成统一的意见进行展示.

第一步（把“增大”符号化）：当x1＜x2时，y1＜y2.

第二步（把“随”符号化）：当x1＜x2时，f（x1）＜f（x2）.

第三步（把“任意”符号化）：

是否可以联想个别数值对单调性进行一定的说明呢？例如函数y=x2（x∈R），若x=-1，2，3，4，…，则y=1，4，9，16，…，函数值y随着x的增大而增大这一说法正确吗？

对区间I上有限或无限个自变量满足x1＜x2，且f（x1）＜f（x2），都无法将“函数值y随着x的增大而增大”的本质反映出来，因此必须强调x1、x2的任意性才能将单调递增的特征准确表述出来，对任意x1＜x2都有f（x1）＜f（x2）.

第四步（把“区间”符号化）：

x1、x2在“任意”二字的含义范畴内还有着“不任意”的表现与含义，函数的单调性这一局部性质表明其与区间密不可分，此时须强调定义中x1、x2∈I.

对于区间I内的任意两个值x1、x2，当x1＜x2时，都有f（x1）＜f（x2）.

最后是小组发言.

函数的单调性这一概念的构建在本课的教学活动中经历了两个关键的过程.

第一个关键的过程是函数单调性意义的构建，学生在若干函数图像的观察中运用自然语言对函数图像的特征进行描述并不是很困难的一件事，因此，这一过程的构建相对来说是这一概念学习完整过程中相对较为容易的.教师在本课的教学活动中一共设计了四个函数并引导学生对其图像进行了观察，使学生在教师的启发与图像观察的过程中获得函数图像的上升与下降展现单调性这一函数基本性质的认知.

第二个关键过程是运用数学符号将单调性的意义完整、精确地表示出来，这个过程对于学生来说是有一定难度的.用数学符号对函数自变量x增大时函数值y增大或减小的动态过程进行描述是这一过程中最重要、最关键的环节，其不仅要将变化规律描述清楚，描述还应做到完整、准确而简洁.学生在经历静态的数学符号描述静态数学对象直至动态数学对象之时所受到的思维挑战是比较巨大的，这对于高一新生来讲确实很有挑战性，因此，这一过程的知识构建需要教师首先准确把握学生思维的“最近发展区”，着眼于学生的发展进行有意义的构建以促进学生对知识难点的把握，本课中的层层设计有效地引导了学生的思维，并顺利突破了这一难点.

三、深入探索，加深理解

教师在这一定义的教学中需要重点注意三个层面含义的把握并引导学生领悟：

（1）函数单调性的定义.一般来说，设函数y=f（x）的定义域是I，区间A⊆I：如果对于区间A内的任意两个值x1、x2，当x1＜x2时，都有f（x1）＜f（x2）或f（x1）＞f（x2），也就是说函数f（x）在区间A上是增加或减少的，因此，函数f（x）的单调递增或递减区间就是A.

教师在教学中尤其需要把握“区间A⊆I”、“任意”、“都”这几个关键词所代表的具体含义.

区间A⊆I的存在意味着函数单调性的判断首先必须对其进行定义域的判断，也就是说，单调性和“区间”是密切相关的，区间不同，函数所展现的单调性也会不同.因此，教师在函数单调性的教学中尤其要引导学生注意以下内容：如果f（x）在区间I1上为增函数，在I2上也为增函数，这并不代表（fx）在区间I1∪I2上就一定会是增函数.例如，函数在（-∞，0）上为减函数，在（0，∞）上也为减函数，不过在（-∞，0）∪（0，∞）上却不是减函数，（f1）＞（f-3）就能很好地说明这一点.

“任意”两个字包含着“整体”的含义，但这必须是建立在某一区间上进行体现的，所以定义中的x1、x2具有任意性且不能用特殊性来代替，不过用来否定函数是增函数或是减函数时还是适用的；“都”在这一概念中的出现表达的是“无一例外”的意思，需要强调的是区间这一条件的表达.由定义的充要性可知，由（fx）是增（减）函数且（fx1）＜（fx2）可以得出x1＜x（2x1＞x2），由此我们应该能够感知自变量与函数值之间不等关系的正逆互推，而且这正是因为函数的单调性而决定的.

（2）单调性.假如函数y=（fx）在定义域的某个子集上会增加或减少，则函数y=（fx）在该子集上就具备单调性.函数单调性概念的学习也是数列单调性概念的铺垫性学习.

（3）假如函数y=（fx）在整个定义域内增加或减少，则该函数就可称为增函数或减函数，单调函数是其统一的称谓.

总之，本课教学设计的主线很明确，也就是函数的单调性的概念，整个教学活动以及学生的学习活动都是紧紧围绕这一主线而得以落实的，贯穿整个课堂的函数单调性概念的教学将数形结合与几何直观的思想进行了充分的展现，学生在情境导入、抽象概括、深入探索这三个环节的学习中也获得了函数单调性这一概念的深刻思考与掌握.