从“稚化思维”走向“智化思维”——以“一类函数零点问题”为例

☉浙江省象山县第二中学 吕增锋

☉浙 江 省 象 山 中 学 林薇薇

相对于学生而言，教师是“专家”，知识渊博，思维活跃，各种解题方法信手拈来，但是对教师而言，却容易忽视学生作为“初学者”思维幼稚与不成熟的一面，往往喜欢把自己的思维理解方式强加给学生，把自己所认为的正确观点和好的解题方法直接告诉学生，从而导致教师的“教”与学生的“学”严重脱节.这种现象在数学解题教学中尤为突出，教师常常因为过于追求解题方法的“短、频、快”，忽视问题的探索过程，一味地“灌输”解题技巧，从而无法使学生的数学思维能力得到有效提升.于是，教师有效地“稚化”自己的思维，隐蔽自己的外在权威，悬置自己拥有的知识，不以“专家”自居，而是有意识地把自己的思维降格到与学生相仿的水平，退回到初学者的状态，把熟悉当成陌生、把再次授课当成首次接触，设身处地地揣摩学生的认知状况和思维特点，以平等身份和学生一起寻找攻克难关的对策就显得尤为迫切.

一、理解通法，展现思维共性

在解题教学中，很多教师习惯于把“最好”的方法教给学生，而忽视了通解通法在发展学生思维能力时的重要价值；很多教师习惯于把各种解法“一股脑”地展现给学生，而忽视了一题多解容易导致思维过度分散的副作用.因此，通解通法是解题教学的切入口，它有助于理解发现学生的思维动向，有助于教师从学生原有知识和经验中找到向“最近发展区”发展的“支架”，把课堂变成师生共同提出问题、解决问题的阵地，促进学生积极参与课堂探究活动，让学生在亲身经历的活动中了解数学知识的发生、发展过程.

问题：已知函数f（x）=x2+ax+b（a，b∈R）在区间（0，1）内有两个零点，则3a+b的取值范围是______.

分析：本题主要考查二次函数的图像、函数的零点、不等式及利用线性规划求范围等知识点，意在渗透数形结合思想、化归与转化思想，提高运算求解能力.

通法：由题意得：

图1

其对应的平面区域如图1所示.

易知3a+b∈（-5，0）.

利用线性规划知识，借助数形结合思想是解决此类问题的通法，也是学生固有的思维方式，它是教师进行教学设计时的重要依据之一，教师能否把握好学生的思维心理和思维特点，能否对学生接受知识的心理作出切合实际的判断，是教师解题教学成功的关键所在.

二、构造变式，引发思维冲突

如果教师平铺直叙地传授新的解题方法，就很容易演变成教师个人的“绝活”表演，而学生只能成为置身事外的观众.在这样的情境下，再好的数学方法与数学思想也无法激起学生的兴趣，教学效果就会大打折扣.如果教师通过构造变式，故意给学生制造解题障碍，使得学生原有的解题方法变得不再“合适”，从而引发思维冲突，迫使学生去寻找新的方法.

变式1：已知函数f（x）=x2+ax+b（a，b∈R）在区间［0，1］上有两个零点，则a2-2b的取值范围是______.

变式2：已知实数a，b满足0＜a-b≤1，且函数f（x）=x2+ax+b（a，b∈R）在区间（0，1）上至少有一个零点，则3a+b的取值范围是______.

分析：变式题的基本解答套路虽然与原题类似，但比较麻烦的是变式1对于“a2-2b”的几何意义的理解令很多学生一筹莫展，而变式2涉及了分类讨论思想，要把“有零点”情况分为两类：“1个零点或者两个零点”，这样解题的过程相对就比较烦琐了.于是，就引发了学生对于“其他”简便解法的思考.

“稚化思维”要求教师把思维的触角深入到学生的思维领地，进行发掘和研究，想学生所想，惑学生所惑.因此，根据教学需要，教师蓄意制造可引起迷惑的思维环节，并且在教学难点处，教师装作一筹莫展的样子，通过“设疑——析疑——释疑”的方式来激发学生的求知欲.

三、回归本质，促进思维共鸣

通常情况下，数学题目存在着多种解题思路，从表面上看这些解题方法形式繁多，让人眼花缭乱，但无论哪种解题方法其都根植于数学问题的本质.先搞清楚问题的实质，然后通过不同角度的分析，就会产生不同的解题方法，从而引发师生思维的共鸣.

回归原题，它的本质是函数零点问题的延伸，而零点既可以看成是方程的“根”，也可以理解为两个函数图像之间的“交点”，从思想方法层面上看，“根”、“零点”、“交点”之间的转化实质上就是数与形之间的相互转化.通常情况下，解决此类问题是把“根”转化为“零点”或者“交点”，把“数”转化为“形”，那我们能不能反其道而行呢？

巧法1：把零点转化为根

令方程f（x）=0的两个根为x1，x2，则f（x）=x2-（x1+x2）x+x1x2，所以a=-（x1+x2），b=x1x2，则3a+b=-3x1-3x2+x1x2=（x1-3）（x2-3）-9，因为x1，x2∈（0，1），所以3a+b∈（-5，0）.

此法对于变式1也适用，能够迅速得到a2-2b=x12+x22∈［0，2］.

巧法2：把零点转化为交点

因为f（x）=x2+ax+b=0⇒-x2=ax+b，令g（x）=-x2，h（x）=ax+b，即g（x）=h（x），则h（3）=3a+b.于是，问题转化为当g（x）与h（x）有两个交点时，求h（3）的取值范围.如图2所示，可知当直线h（x）=ax+b与g（x）=-x2相切于原点与点（1，-1）是两个临界位置.当相切于点（1，-1）时，容易求得a=-2，b=1，则h（x）=-2x+1，此时h（3）=-5，所以3a+b∈（-5，0）.

此法对变式2也适用，只是与原题相比，变式2多了一组限制条件，反映到图像上就是多了一条临界线段.因为0＜a-b≤1，则-1≤h（-1）=-a+b＜0，如图3所示，则P，Q两点是h（x）=ax+b满足题目条件的临界位置，容易求得3a+b∈（-2，3）.

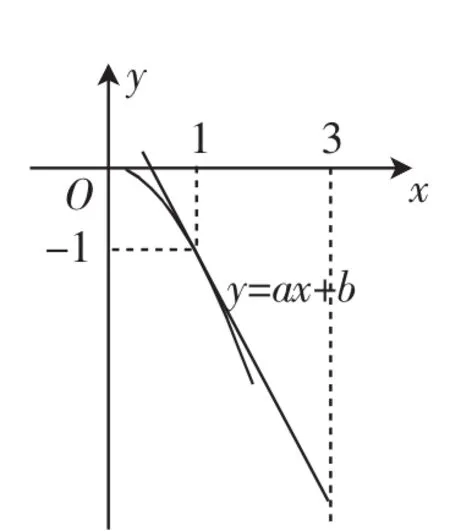
图2

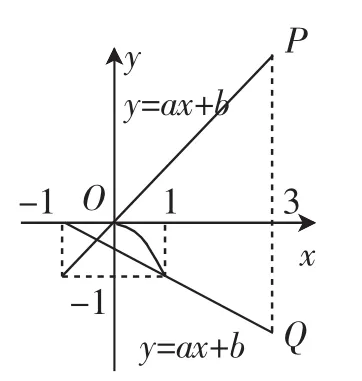
图3

基于“稚化思维”的解题教学一般遵循“旧知识固定点——新知识联结点—新知识生长点”的思维方式进行有序展开，这样就容易让学生将学习新知识的过程转化成为自己意义建构的过程.

四、辨析训练，达成思维共振

解题教学最终目的就是在教师组织下，引导学生学习“专家”思维活动成果，实现学生思维结构向“专家”思维结构的转化.为了顺利实现这种转化，例题分析后的“辨析应用”是必不可少的，它可以在“专家”与学生思维活动之间架设认知的桥梁，使师生之间在认识程序上达到“同频”，引起教与学的思维“共振”.

经过前面的学习，学生已经基本掌握了这类函数零点问题的解题方法，具体如图4所示，但在实际解题过程中究竟如何灵活选择合适的解题方法还需进一步明确，因此，结合例题进行针对性的辨析训练是必不可少的.

图4

例1已知函数（fx）=x2+ax+b（a，b∈R）在区间［-1，1］上有零点，且满足0≤b-2a≤1，则b的取值范围是______.

例2已知函数（fx）=x2+ax+b（a，b∈R）在区间［0，1］上有零点，则ab的最大值是______.

例3已知a，b∈R且0≤a+b≤1，函数（fx）=x2+ax+b在］上至少存在一个零点，则a-2b的取值范围为______.

分析上述三道例题的特点，就会发现，例1与例2适用于“巧法2”，因为它们能够构造出对应的直线与抛物线，b-2a可以转化为h（-2），而而例3适用于“巧法1”，a-2b可以表示为x1，x2的函数.

教师“稚化”自己的思维，以学生的思维方式为教学的起点，惑学生之所惑、难学生之所难、错学生之所错、思学生之所思，从而降低数学理解的门槛，促进知识的自然生成，最终达到“智化”学生思维的目的.