关注数学活动经验 提升学生思维能力
—— 以一节椭圆性质探究课为例
☉江苏省启东中学 胡 勇
一、引言
基本活动经验是数学课程标准中提出的“四基”之一,也是近年来教育教学研究的热点,相关的研究论文很多.在众多研究结果中,对数学活动经验的认识和理解还存在着一定程度的差异,但在以下两个方面却基本上保持一致.
一是对数学活动经验的价值认同,即“数学活动的过程不仅能够加深学生对数学概念、性质、定理的理解,同时数学活动经验的积累也是形成学生创新能力的基础.”
二是对数学活动经验的形成机制,即“学生的数学活动经验是在做数学的过程中形成的,它的产生和形成实质上是学生经历数学活动的过程.”
下面以笔者近期在本校开设的一节市级公开课为例,谈谈对促进学生数学活动经验积累的探索和思考.
二、基本情况分析
1.教学内容分析
直线与椭圆的位置关系是学生学习的难点之一,主要表现在:对问题的本质理解模糊,只知“埋头运算”,不知“抬头识路”,缺乏解题策略的选择意识,往往因为方法不合理而半途搁浅,或因计算过于烦琐而产生厌烦、畏惧心理.针对学生这一普遍存在的困惑,在复习椭圆及其性质后设计本节探究内容,让学生在自主探究的过程中体会解决解几问题的一般策略和方法.
2.教学目标
(2)通过探究椭圆的性质,理解直线与椭圆问题解决一般策略和方法;
(3)了解类比在数学发现、创新过程中的作用,领略数学发现的一般过程和快乐.
3.教学重难点
类比圆的性质得出椭圆的相关结论.
三、教学实录
1.情境引入
师:著名天文学家开普勒曾说过:“我珍视类比胜过任何东西,它是我最可信的老师,它能揭示自然界的秘密,在几何学中,它应该说是最不能忽视的.”开普勒如此推崇类比,可见它在自然科学更多是在数学发展中的重要地位.今天,就让我们一起来运用这一有力武器,探究并发现椭圆中的一些结论.
点评:用伟大科学家的话激发学生学习的兴趣.开场白直接点明类比思想,为接下来的发现之旅指明方向.
2.自主探究,意义建构
探究问题1:如图1,已知圆O:x2+y2=r(2r>0)上两点M,N,且OM⊥ON.在此条件下你能得出哪些结论?类比到椭圆中,你能得出哪些猜想?
学生分组讨论、交流,教师巡视.大约5分钟后由小组指派代表发言.
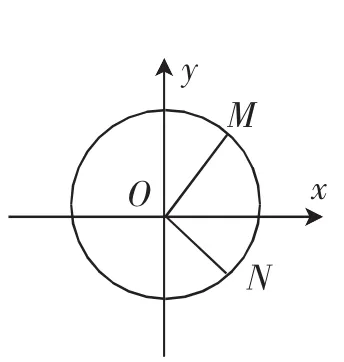
图1
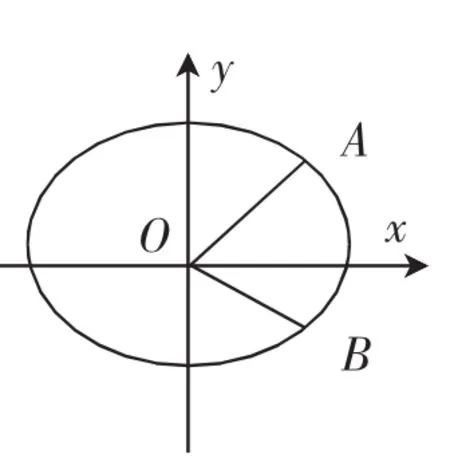
图2
生2(另一小组成员):错了!两直线垂直的条件也要改.
师:怎么改?为什么?
学生独立探究,教师对学习困难的同学进行点拨,大约10分钟后学生展示成果.
生3:猜想成立,证明如下:

故猜想成立.
师:很好.除了上述猜想,同学们还有别的猜想吗?
生4:类比圆中结论OM2+ON2=2r2有OA2+OB2=a2+b2.利用上述证明可得:
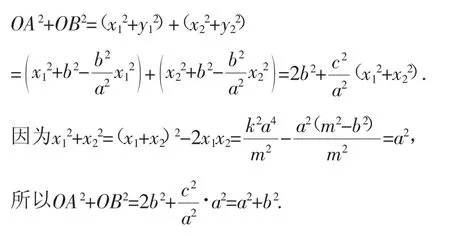
生5:类比圆中弦中点的轨迹还是圆,猜想椭圆中弦AB的中点P的轨迹仍是椭圆.

所以线段AB的中点P的轨迹是椭圆,

探究问题2:想一想圆中与两直线垂直的有关结论,它们可以类比到椭圆中吗?
学生分组探讨、交流,教师参与讨论,适时点拨.大约10分钟后由各组指派同学展示探究成果.
生6:类比“圆中直径所对圆周角是直角”得到:如图3,已知点A,B,P在椭圆上,若直线PA,PB的斜率存在,则A,B关于原点对称
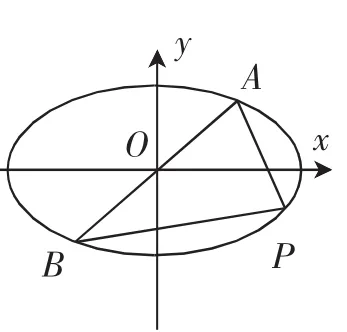
图3
生7:类比“圆中平分弦(不是直径)的直径垂直于弦”得到:如图4,已知与坐标轴不垂直的直线l与椭圆交于点A,B,线段AB的中点为M,则

图4
证明如下:设M(x0,y0),则
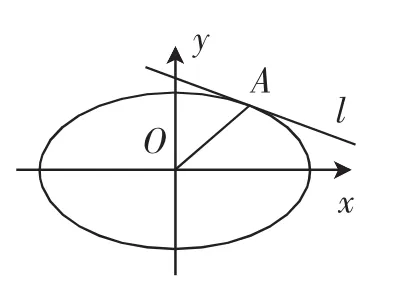
图5
点评:从探究的空间、时间、层次等方面为学生营造了一个较为宽松的探究情境,使得整个探究过程基本上自成体系、有序、环环相扣,各个探究过程之间密切相关,做到由浅入深、由易到难、由现象到本质.
师:请同学们总结一下,我们得到哪些结论.
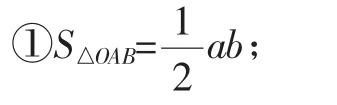
②OA2+OB2=a2+b2;
点评:数学知识是可以直接授受的,但数学活动经验却不能传递,只有学生亲身经历自主探究,完整经历数学家发现数学结论的一般过程,才能够切身体会知识发生发展的过程,提高运算求解和思维能力,体验学科研究的一般方法,积累活动经验.
3.反思总结,凸显本质
(1)本节课得到了椭圆的哪些性质?
(2)本节课在证明椭圆有关性质时运用了哪些方法?
(3)本节课得到椭圆性质的过程,遵循了怎样的研究方法和一般过程?
点评:让学生反思经历的数学活动,回顾基本知识、技能,感悟科学研究的一般方法和过程,使得学生所获得数学活动经验由“懵懂模糊”逐渐“清晰明确”,重新建构认知体系.
四、数学活动的几点认识
1.数学活动开展立足于教师的精心预设
成功的课堂教学离不开预设,只有精彩的预设,才能和谐生成.设计什么样的数学活动才能真正提升学生的数学活动经验呢?
首先,要对学生原有认知结构中的数学活动经验进行分析与联结.数学学习的类似性使得储存在学生头脑中的数学活动经验具有很强的迁移性和认同性,因此在分析数学知识、数学技能、数学学习心理特征时,还应将学生数学活动经验分析纳入学情分析的范围.
其次,结合学情和教学内容确定数学活动经验积累的具体、可行的目标.目标解析采用条目式,以求简洁、准确表达“理解”、“掌握”的具体内容.
最后,合理设计数学活动的各个环节.活动的进程设计除了观察、实验、操作、探讨和交流等操作层面外,更要注重数学活动背后蕴涵的数学思维活动,“数学活动经验的核心应是数学思维活动经验.”
2.数学活动经验生成于学生的自主探究
数学活动经验是动作和心智交互作用的结果.学生是学习的主体,教师要注意角色定位的转换,由传统的知识传授者转向现代的学生发展的促进者.教师的角色应定位在组织指导者、合作交流者,课堂是复杂的,运动变化的,由于多种不确定因素的存在和相互作用,“预设”不可能穷尽课堂所有可能的变化.当学生遇到这样那样的挫折和失败需要得到帮助时,教师应该鼓励、引导.
3.数学活动经验提升于学生的反思悟透
弗莱登尔说过:“反思是数学思维活动的核心和动力,没有反思,学生的理解就不可能从一个水平升华到更高的水平”.学生在经历数学活动后,所形成的数学活动经验是懵懂模糊的,只有对数学知识形成过程中体现的研究方法和研究经验进行适当的总结和反思,才能进行合理的知识建构,才能提高自己的思维能力,才能使所获得的数学活动经验更加清晰明确.教师作为教学的主导者、帮助者、引导者,一定要有反思的意识和习惯,要多在反思体验处构建数学活动经验,以促进学生认知结构的发展.

