我国金融产业集聚与经济增长关系的实证分析

张克雯

（贵州财经大学 金融学院，贵阳 550004）

0 引言

当前，国内外学者在金融产业集聚与经济增长的关系研究上取得了较为全面和系统的理论成果，主要体现在以下三个方面：一是认为世界经济能够如此快速发展，其核心动力在于金融机构对初创型公司提供了金融资产信贷的帮助[1]；二是在数据分析过程中发现金融产业集聚和经济增长存在一定程度的正相关关系，即金融产业集聚程度越高、金融体系越完善、金融企业数量越多，经济发展水平越高[2]；三是认为金融产业集聚可以借助需求和资本关系促进区域经济发展，通过构建金融产业集聚发展水平指标、建立VAR模型等手段，得出金融产业集聚与经济增长有着明显的相互促进作用关系[3-5]。

但当前研究成果鲜有通过双向互动的视角展开深入研究，因此，本文构建了金融产业集聚与经济增长的双向互动模型，对金融产业集聚与经济增长的内在关系进行实证分析，并从金融角度得出了与经济增长相互促进的结论。

1 模型构建、变量选取和数据说明

1.1 模型构建

本文根据相关的经济增长理论，构建经济增长和金融产业集聚影响因素之间的双向互动关系模型[6]，其模型方程为：

其中，G为社会经济增长率，D为经济集聚强度，XG为影响经济增长的因素，XD为影响经济集聚强度的因素。

1.1.1 经济增长模型

为了具体说明我国经济增长的影响因素，并体现金融产业集聚对经济增长的作用，本文选取以下因素作为影响我国经济增长的关键因素：金融产业集聚水平（FIAL）、金融投资（FI）、人力资源（HR）、财政水平（FIN）、基础设施（INF）和人口密度（PD）。据此，本文构建如下经济增长模型：

其中，i为样本数据的金融中心城市，t为时间，αg为总控制变量，φi1、φi2、φi3、φi4、φi5、φi6为经济增长影响因素的参数，εi，t为经济增长误差值。相应的影响因素是：FIAL为金融产业集聚水平因素、FI为金融投资因素、HR为人力资源因素、FIN为财政水平因素、INF为基础设施因素、PD为人口密度因素。

1.1.2 金融集聚影响因素模型

相对而言，经济增长会直接影响金融产业集聚。因此，以大城市为例，本文的金融集聚影响因素模型的基本形式为：

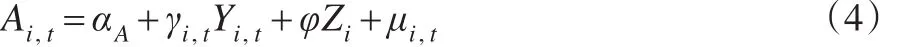
其中，Ai，t为第i个城市在第t年的金融产业集聚水平，Yi，t为第i个城市在第t年的金融集聚影响因素，Zi为金融集聚影响因素的控制变量，αA、φ、γi，t为参数，μi，t为第i个城市在第t年的金融集聚误差值。

为了具体说明我国金融集聚的影响因素，并体现金融产业集聚对经济增长的反作用，本文选取国内生产总值（GDP）、金融投资（FI）、人力资源（HR）、对外开放程度（OTOW）、基础设施（INF）和人口密度（PD）作为影响我国金融集聚的关键因素。因此，金融集聚影响因素模型的具体表达式为：

其中，i为样本数据的金融中心城市，t为时间，αA为总控制变量，γi1、γi2、γi3、γi4、γi5、γi6为经济增长影响因素的参数，μi，t为金融集聚误差值。相应的影响因素是：GDP为国内生产总值因素、FI为金融投资因素、HR为人力资源因素、OTOW为外开放程度因素、INF为基础设施因素、PD为人口密度因素。

1.2 变量选取和数据说明

GDP表示国内生产总值，反映一段时间内生产和制造的全部产品和服务的市场价值。FIAL表示金融产业集聚水平，它通过金融集聚城市的发展规模和人口密度等指标衡量。因此，本文选择金融产业集聚区位熵衡量法对金融中心城市的金融产业集聚水平进行衡量。此外，本文选择金融投资（FI）来体现金融企业发展业务等方面的资金流动；选择人力资源（HR）来体现每万人中接受过高等教育的人数；选择财政水平（FIN）来体现政府实际的财政支出能力；选择基础设施（INF）来体现政府投入社会的公共服务财力；选择人口密度（PD）来体现每平方公里中的人口数量；选择对外开放（OTOW）来体现金融企业与国外企业合作的投资。

本文研究对象为我国地级市以上（包括地级市）的金融中心城市。样本数据选择2008—2016年我国10个大中小型金融中心城市的国内生产总值（GDP）、金融产业集聚水平（FIAL）等变量数据[7]。10个金融中心城市为：北京、上海、深圳、广州、天津、重庆、济南、南京、杭州、沈阳。另外，金融产业集聚水平可以通过金融产业附加值的高低来体现。

2 实证分析

2.1 单位根检验

单位根检验可以检验模型变量的平稳性。而在判断样本数据之间的协整关系之前需要进行单位根检验。在建立金融产业集聚与经济增长关系的数据模型前需要采用相关的单位根检验法对样本数据的平稳性进行检验。为了避免单一的单位根检验法造成的偶然性，本文将选择如下单位根检验方法对样本数据进行检验：LLC检验、Hadri检验、IPS检验和Fisher-ADF检验[8]。单位根检验结果如表1所示。

从表1可以看出，样本数据无单位根，即单位根数据稳定，满足协整检验的基本要求，可进行后续协整检验。

2.2 协整检验

协整检验可以判断多组样本数据在线性组合后是否具有了稳定性。本文采用Pedroni检验和Kao检验法[9]对金融产业集聚与经济增长的关系进行协整检验，判断是否具有协整关系。

首先对经济增长模型进行协整检验，相关模型中的参数变量的Pedroni检验和Kao检验结果如表2所示。

表1 样本数据的单位根检验结果

表2 经济增长模型协整检验结果

设原假设样本数据不存在协整关系。从表2可以看出，Pedroni检验和Kao检验的8个检验中有6个否决了原假设，可以认为经济增长模型中，金融产业集聚水平、金融投资、人力资源、财政水平、基础设施和人口密度与经济增长之间存在协整关系。

之后对金融集聚影响因素模型进行协整检验，协整检验结果如表3所示。

表3 金融集聚影响因素模型协整检验结果

同样设原假设样本数据不存在协整关系。从表3可以看出，Pedroni检验和Kao检验的8个检验中有5个否决了原假设，可以认为金融集聚影响因素模型中，国内生产总值、金融投资、人力资源、对外开放程度、基础设施和人口密度与金融产业集聚水平之间存在协整关系。

2.3 参数估计

2.3.1 经济增长模型参数估计

本文使用固定因素模型法分析金融产业集聚因素对经济增长的作用效果。经济增长模型的参数估计结果如下页表4所示。

从表4可以看出，模型一未加入金融产业集聚因素（FIAL）进行参数估计，而模型二加入了金融产业集聚因素（FIAL）进行参数估计，两个模型进行比较与分析。当样本数据未考虑金融产业集聚因素（FIAL）时，只有金融投资（lnFI）的P值不显著，其他变量均体现出显著特征；调整R2的值，此时F检验结果显著，提高了总体数据的拟合度。当样本数据考虑金融产业集聚因素（FIAL）时，即模型二所示，调整R2的值，使其略高于模型一的对应值，总体数据拟合度也较高。因此，在经济增长模型中，金融投资（FI）、人力资源（HR）、财政水平（FIN）、基础设施（INF）和人口密度（PD）对经济增长起到了一定的促进作用，而金融产业集聚水平（FIAL）的促进作用更加明显。

10个样本金融中心城市的经济增长的综合因素作用和金融产业集聚因素作用结果如表5所示。

表4 经济增长的固定因素模型参数估计结果

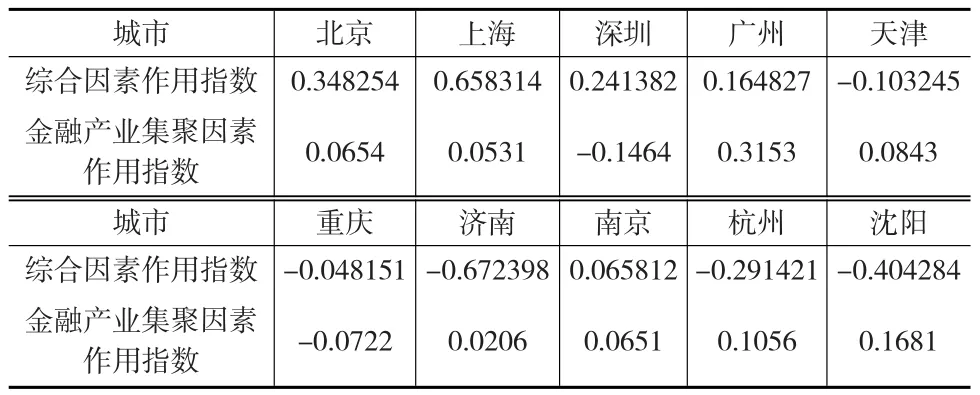
表5 样本城市经济增长综合因素和金融产业集聚因素作用结果

从表5中可以看出，10个城市中经济增长的综合因素作用最大的是上海、北京和深圳。而金融产业集聚因素作用结果的差异性较为明显，深圳和重庆的金融产业集聚因素作用结果表现为负相关。对于其他城市而言，金融产业集聚因素作用对经济增长起到了一定的推动作用。

2.3.2 金融集聚影响因素模型参数估计

金融集聚影响因素模型是用于研究国内生产总值等金融因素对金融产业集聚的影响效果，为了突显国内生产总值因素对金融产业集聚的影响，本文同样采用固定因素模型法分析国内生产总值因素对金融产业集聚的作用效果。金融集聚影响因素模型的参数估计结果如表6所示。

表6 金融集聚影响因素的固定因素模型参数估计结果

从表6可以看出，调整R2的值为0.955772，F检验结果显著，总体数据拟合度较高。因此，在金融集聚影响因素模型中，国内生产总值（GDP）、金融投资（FI）、人力资源（HR）、对外开放程度（OTOW）、基础设施（INF）和人口密度（PD）对金融产业集聚有着较强的促进作用。特别是国内生产总值因素，经济增长加快也能吸引更多的金融机构进行金融产业集聚，符合本文的实证结论。

10个样本金融中心城市的金融产业集聚的综合因素作用和经济增长因素作用结果如表7所示。

表7 样本城市经济增长综合因素和经济增长因素作用结果

从表7中可以看出，10个城市中经济增长的综合因素作用最大的是北京、南京、沈阳、广州和济南。而经济增长因素作用结果的差异性也较为明显，沈阳、广州、深圳和南京的经济增长因素作用结果表现为正相关，经济增长对金融产业集聚作用明显。对于其他城市而言，经济增长对金融产业集聚的影响为负值，表明经济增长和金融产业集聚已经出现了反向作用。

3 结论

本文把经济增长和金融产业集聚的关系作为研究对象，构建了经济增长和金融产业集聚影响因素之间的双向互动关系模型，并分析了金融产业集聚和经济增长的相互影响程度。实证结果显示，一方面，金融产业集聚确实能促进经济增长，而金融产业集聚程度不同，对城市经济增长的影响也存在较大差异，样本中的10个城市金融产业集聚促进了城市经济增长的效果，排名为：广州、沈阳、杭州、天津、北京、南京、上海、济南；另一方面，经济增长也会促进金融产业集聚，样本中的10个城市经济增长对金融产业集聚有明显促进作用的是：沈阳、广州、深圳和南京。因此，金融产业集聚和经济增长表现为相互促进作用。