基于改进的SOS算法的反时限过电流保护协调优化

白祥昌，吕飞鹏，杨常

(四川大学 电气信息学院， 成都 610065)

0 引 言

反时限过电流保护根据不同的短路电流有不同的动作时限。传统的反时限过电流保护采用查表法、泰勒级数分解法等方法来设置继电器的参数，但是传统方法计算速度较慢、计算精度较低[1]，难以解决复杂问题。

针对于此，相关学者已经提出把继电器的参数整定计算转化为优化问题，采用简单线性规划、遗传算法、改进粒子群算法[2]等方法来解决。然而，传统的优化算法对于含有较多约束条件的复杂问题仍然存在一些缺陷[3]。文献[4]采用遗传算法来求解离散型继电器的时间整定值TDS(Time Dial Settings)，但是遗传算法的计算速度较慢而且稳定性不高。文献[5]采用PSO算法来整定计算，但是采用PSO算法容易出现早熟收敛的情况，局部搜索能力较差。文献[6]采用搜寻(Seeker)算法来优化保护定值,该算法自适应确定搜索方向和搜索步长，能收敛但难以保证收敛到全局最优解。文献[7]提出共生生物搜索算法(SOS)来优化保护设定值，搜索速度快，鲁棒性好，但容易陷入局部最优解。

文中将反时限过电流保护的整定计算转化为一种优化模型，将主保护和后备保护之间的协调问题转化成约束条件，将主保护和后备保护动作时间总和作为优化的目标函数。采用改进的SOS算法对保护定值进行优化，并且和SOS算法以及Seeker算法的整定结果进行了分析对比。

1 继电器保护协调方案

1.1 目标函数

电力系统发生故障时，要求保护装置能够快速、准确的切除故障，在最短的时间将故障隔离到最小的范围内[8]。因此，继电保护的整定优化就是要求保护设备在满足相互配合的基础上，各继电器的动作时间之和加权最小，则目标函数可表示为：

( 1 )

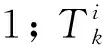
在文中的保护协调优化方案中，反时限特性采用一般形式[9]。通过对继电器的TDS和Ip同时进行优化设置，来减小所有继电器的动作时间，由此目标函数可以表示为：

( 2 )

1.2 限制条件

为了满足主保护和后备保护之间的选择性，要求主保护和后备保护之间需要有一定的时间差(CTI)，即：

Tj,k-Ti,k≥CTI

( 3 )

式(3)通过一个时间级差CTI来保证继电器之间的相互配合；Ti,k是继电器Ri在故障点k点的动作时间，继电器Ri作为主保护；Tj,k是继电器Rj在故障点k点的动作时间，继电器Rj作为继电器Ri的后备保护。CTI的变化范围为0.2 s～0.5 s。文中CTI取值0.3。

通常TDS的变化范围是0.1～1.1，TDS满足以下条件：

TDSi,min≤TDS≤TDSi,max

( 4 )

Ip应该满足以下条件：

Ipi,min≤Ip≤Ipi,max

( 5 )

式中Ipi,min和Ipi,max分别是继电器Ri的最小启动电流和最大启动电流。Ip的设定范围也可以如下表示：

k1IL.max≤Ip≤k2Ik.min

( 6 )

Ip的设置应该确保保护装置在最大负载电流时不误动，在最小故障电流时能够及时动作，式(6)中k1为可靠系数、k2为灵敏系数。

继电器动作时间应满足以下条件：

Ti,min≤T≤Ti,max

( 7 )

式中Ti,min和Ti,max分别是继电器的最小和最大动作时间。

2 改进SOS算法

2.1 SOS 算法

SOS算法是陈明远和Doddy Prayogo在2014年提出用于解决优化问题的一种新算法。SOS算法主要包括三个阶段：互利共生阶段、共栖阶段、寄生阶段。在每一个阶段，每个生物都有随机利用其他生物的可能性。在第一阶段，生物与生物之间互利共生；第二阶段中，一种生物获得有利地位，另一种生物处于中立地位；第三阶段，第一种生物处于优势地位，另一种生物处于劣势地位。

假设Xi是生物圈中的第i类物种，Yj是生物圈中与Xi存在共生关系的第j类生物。在第一阶段中，两类生物处于初始状态Xi和Yj。

Xi,new=Xi+rand(0,1)×(B-M×BF1)

( 8 )

Yj,new=Yj+rand(0,1)×(B-M×BF2)

( 9 )

( 10 )

式中rand(0,1)是0到1之间的随机数；BF1和BF2是有利因子，可以随机选定为1或2；B是初始生态系统中，处于最有利地位的生物；Xi,new和Yj,new分别是物种Xi和物种Yj更新后的状态；M为中间变量，取值为物种Xi和物种Yj的平均值。

在第二阶段中，仍然随机选择两种生物Xi和Yj。Xi要在共生关系中获得优势，而Yj既不获得优势也不会处于劣势地位，处于中立地位。Xi的变化趋势如下：

Xi,new=Xi+rand(-1,1)×(B-Yj)

( 11 )

其中rand(-1,1)是-1到1之间的随机数，只有当Xi,new相比于Xi更有利时，Xi才会更新为Xi,new。Yj仍然处于初始状态Yj。

在第三阶段中，假设仍然随机选择两种生物Xi和Yj。Xi和Yj是属于寄生关系，Xi要处于优势地位，导致Yj处于劣势地位。假设在Xi和Yj更新的过程中，存在因子P，让Xi,new相比于Xi有更好的适应度，让Xi生物处于优势；让Yj,new相比于Yj有更好的适应度，让Yj处于劣势。最终满足Xi占主导地位，而Yj消亡或者被Xi替代。

2.2 SOS-AA算法

Xi和Yj在互利共生阶段部分受到M值的影响或者完全受到M值的影响。在SOS算法的互利共生阶段，M值同时受到有利因子BF1和BF2的影响。BF1和BF2随机选定为1或2。因此，在优化过程中，只有两种变化趋势。有利因子选定为1时，搜索步长短，但收敛较慢；有利因子选定为2时，搜索步长较长，但容易陷入局部最优解。由于有利因子具有不确定性，导致优化结果存在不确定性，因此有必要对有利因子进行改进。

为了克服以上缺陷，文中对有利因子BF1和BF2分别改进为ABF1和ABF2，如下：

( 12 )

改进后，在第一阶段中，两类生物Xi和Yj如下更新：

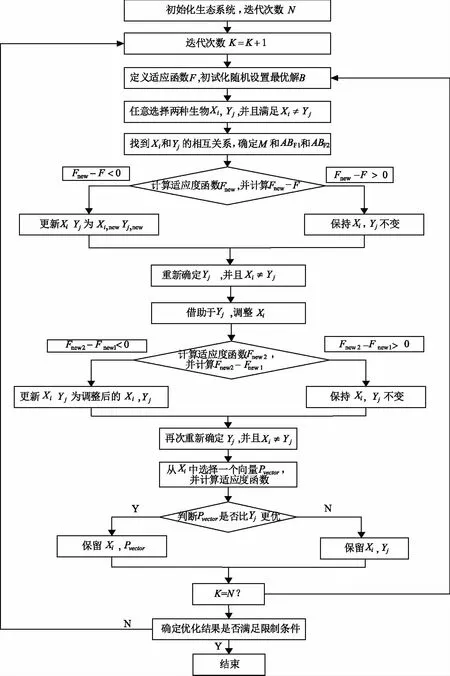
图1 SOS-AA算法程序流程图

Xi,new=Xi+rand(0,1)×(B-M×ABF1)

( 13 )

Yj,new=Yj+rand(0,1)×(B-M×ABF2)

( 14 )

( 15 )

SOS-ABF1-ABF2算法(后文用SOS-AA来代替)能够根据某物种当前的适应度函数FX与生态系统中处于最优位置的生物B的适应度函数FB的比值进行调整，如此改进后，有利因子不再随机选定为1或2，物种的更新状态也不是随机更新，而是根据最优物种来进行自适应调整，由于生态系统中的最优物种的状态始终在更新，其他物种的搜索方向都自适应趋向于最优物种，这样能更快得到最优解。因此，SOS-AA算法不仅可以提高收敛速度，也能够克服解陷入局部最优，减小了优化结果的不确定性。

SOS-AA算法步骤如下：

步骤1：生态系统初始化。随机选择生态系统的大小N(生物种类数量)，初始化决策变量，明确约束条件；

步骤2：确定初始生态系统中处于最优地位的生物B；

步骤3：互利共生阶段。从生态系统中随机选择两类生物体Xi和Yj，根据式(13)和式(14)对Xi和Yj进行改进，得到Xi,new和Yj,new，并且根据式(15)计算出M。计算适应度值，根据适应度值来决定是否接受改进值；

步骤4：共栖阶段。从生态系统中随机选择一种生物Xi，根据式(11)对生物状态进行改进，计算适应度函数，根据适应度值来决定是否接受改进值；

步骤5：寄生阶段。从生态系统中随机选择一种生物Xi，另一种生物Yj变异成P。计算适度值，根据适应度值来决定是否接受变异值P；

步骤6：如果当前Xi不是生态系统中的最后一类生物体，移至步骤2；

步骤7：如果满足收敛条件，停止程序；否则，移至步骤2。

SOS算法与SOS-AA算法的决策变量TDS和Ip的初始值都是在满足上下限范围内的随机值，生物种类N选择20。SOS-AA算法对应的流程如图1所示。

3 案例仿真与分析

文中针对线路中点的三相短路故障进行了仿真分析，IEEE 3节点系统与IEEE 8节点系统分别如图2和图3所示。

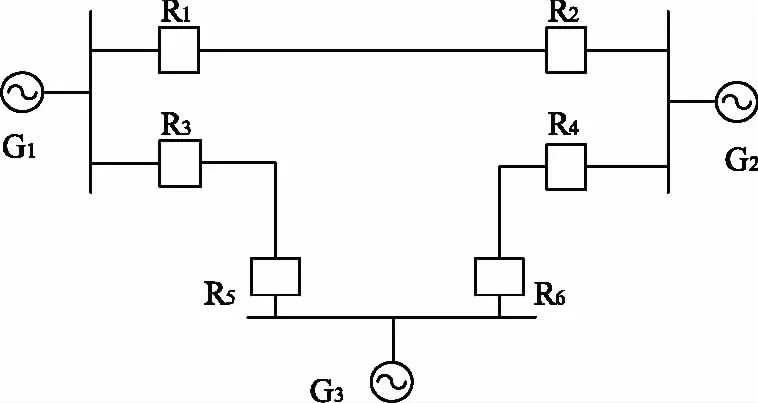
图2 IEEE 3总线系统

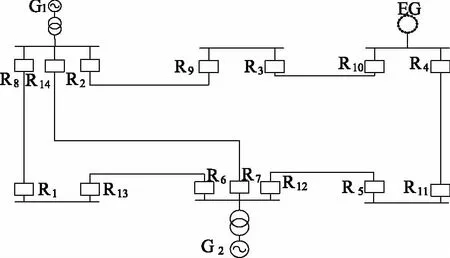
图3 IEEE 8总线系统

图2 IEEE 3节点系统中有三个交流电源，六个过电流保护继电器，详细参数见文献[6]。由于每个继电器均有一对TDS和Ip设定值，因此该案例中共有6个决策变量。

表1为基于Seeker算法、SOS算法和SOS-AA算法的保护优化协调方案TDS和Ip的设定值，通过这些设定值可以算出每种算法对应的主保护和后备保护动作时间及其时间差，如表2所示。

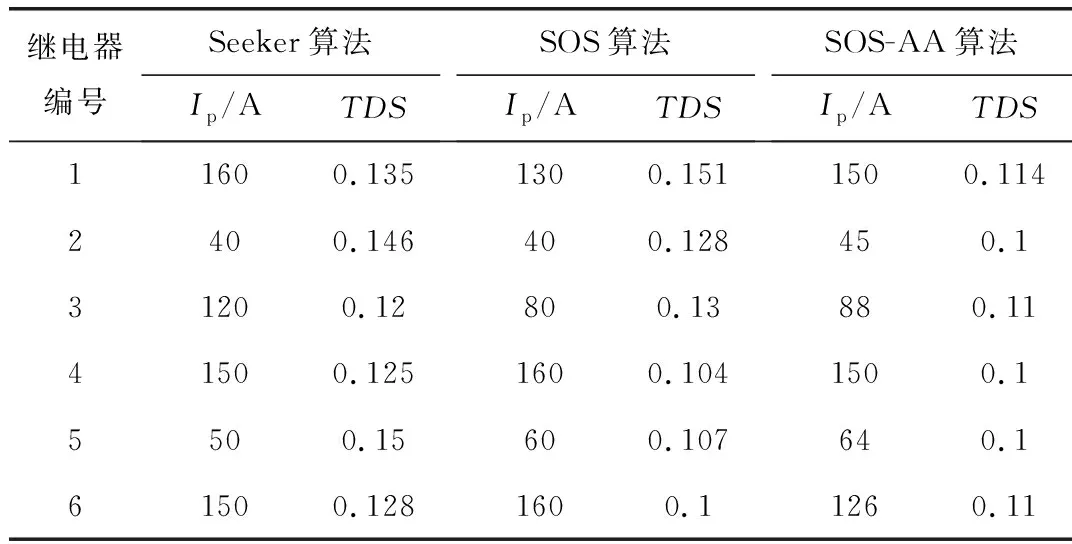
表1 IEEE 3总线系统中继电器的TDS和Ip的优化值

从表2可以得出，基于Seeker算法、SOS算法和SOS-AA三种算法的CTI值均满足限制条件，动作时间总和分别为6.822 s、 5.56 s和4.986 s。

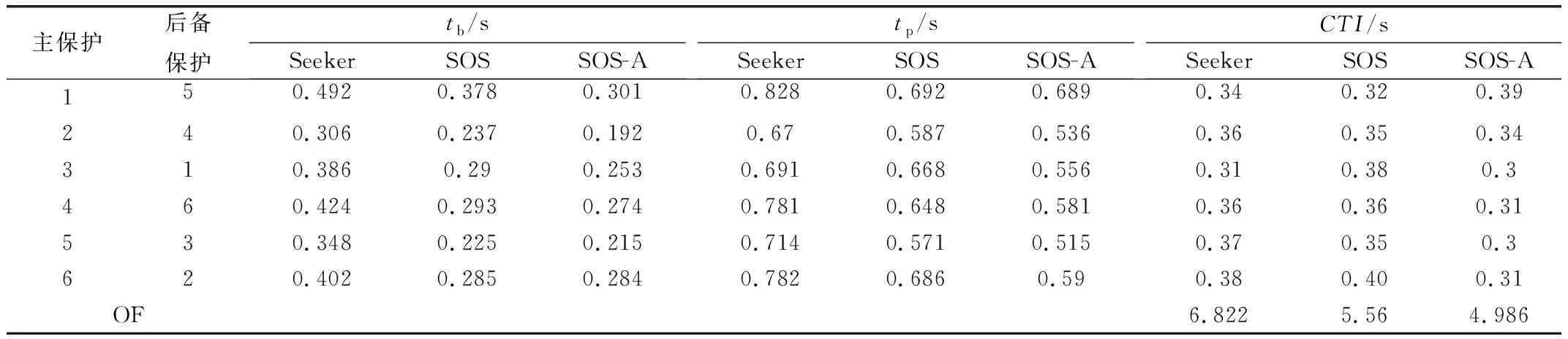
表2 IEEE 3总线系统中主/后备保护动作时间

注：tp表示主保护动作时间，tb表示后备保护动作时间,主表示主保护，后备表示后备保护。

表3中，tp1和tb1分别表示基于SOS-AA算法的主保护和后备保护动作时间，tp2和tb2分别表示基于Seeker算法的主保护和后备保护动作时间，tp3和tb3分别表示基于SOS算法的主保护和后备保护动作时间。从表3可以得出，tp2-tp1、tp3-tp1、tb2-tb1、tb3-tb1均为正值，由此可以得出针对相同故障点，基于SOS算法和Seeker算法所得出的主保护和后备保护动作时间均比SOS-AA算法所得的动作时间长。因此，基于SOS-AA算法所得的保护协调方案在保护满足选择性的同时，能够提高保护速动性。

图3 IEEE 8节点系统中共有三个交流电源，一台变压器，14个反时限过电流保护继电器，28个决策变量，详细参数见文献[10]。基于Seeker算法、SOS算法和SOS-AA算法的保护优化协调方案的所得出的TDS和Ip的设定值，如表4所示，通过优化得到的设定值可以算出主保护和后备保护的动作时间及其时间差，如表5所示。

表5可看出，上述三种算法的CTI值都满足要求，能够满足保护的选择性。在IEEE 8节点系统中，基于Seeker算法、SOS算法和SOS-AA算法所得出的目标函数分别为26.668 s、24.892 s和20.53 s。

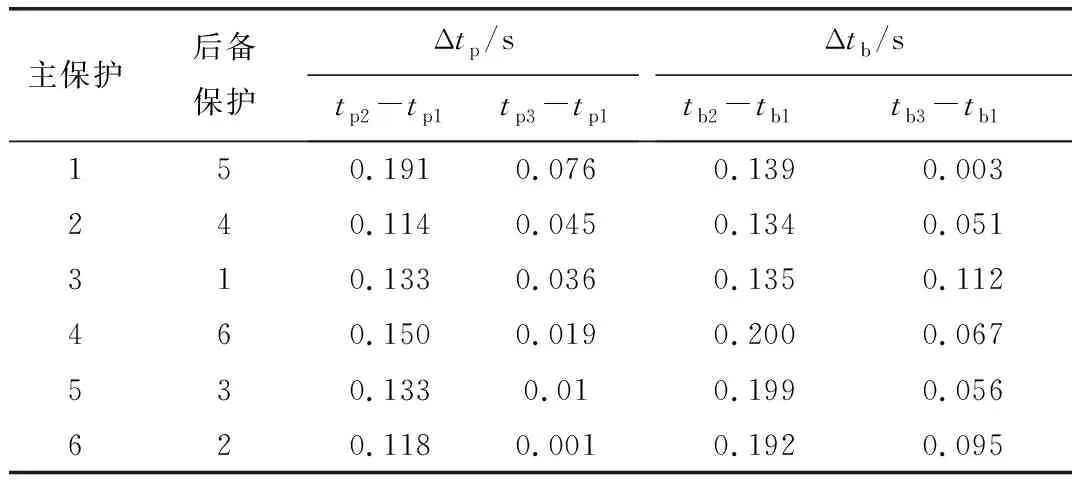
表3 基于Seeker算法、SOS算法和SOS-AA算法的保护动作时间差(3总线系统)

注：tpi与tbi中的i=1、2、3，其中1、2、3分别对应SOS-AA算法、Seeker算法和SOS算法。

从表6中可以看出，tp2-tp1、tp3-tp1、tb2-tb1、tb3-tb1的值均为正，则表明针对相同故障点，基于SOS算法和Seeker算法所得出的主保护和后备保护动作的时间均比SOS-AA算法所得的动作时间长。

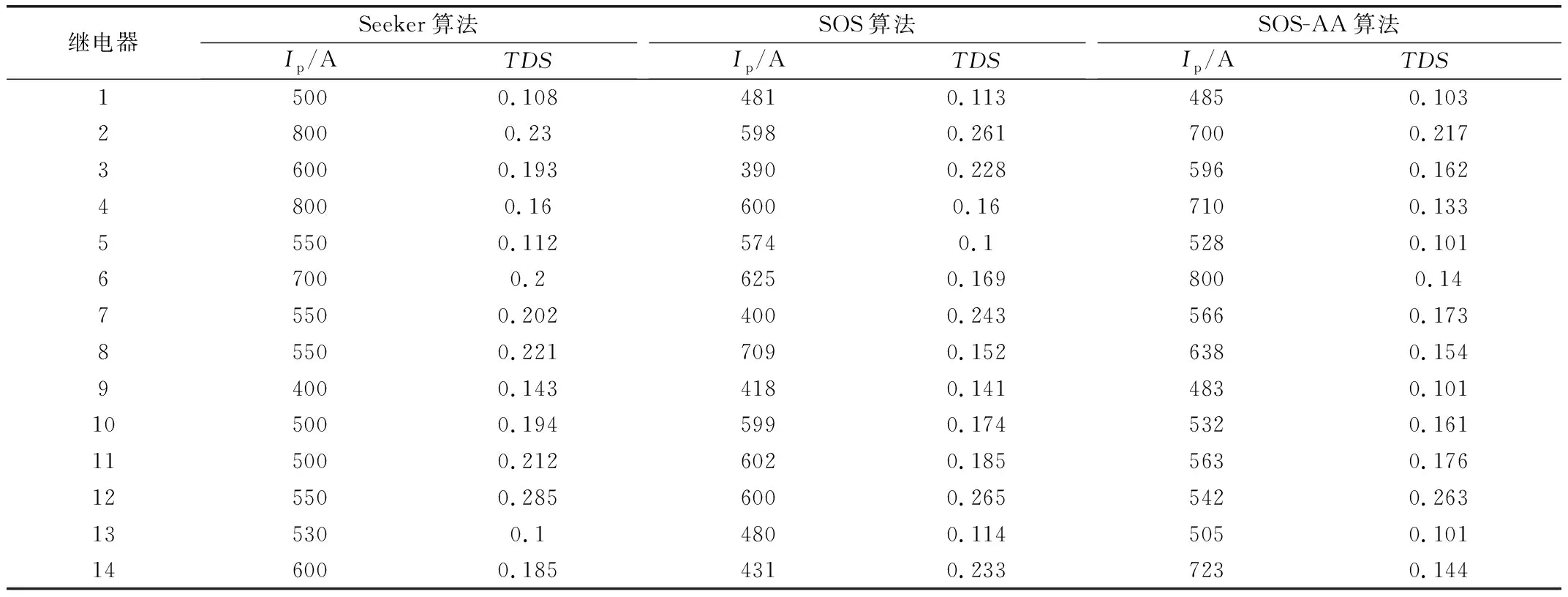
表4 IEEE 8总线系统中继电器的TDS和Ip的优化值

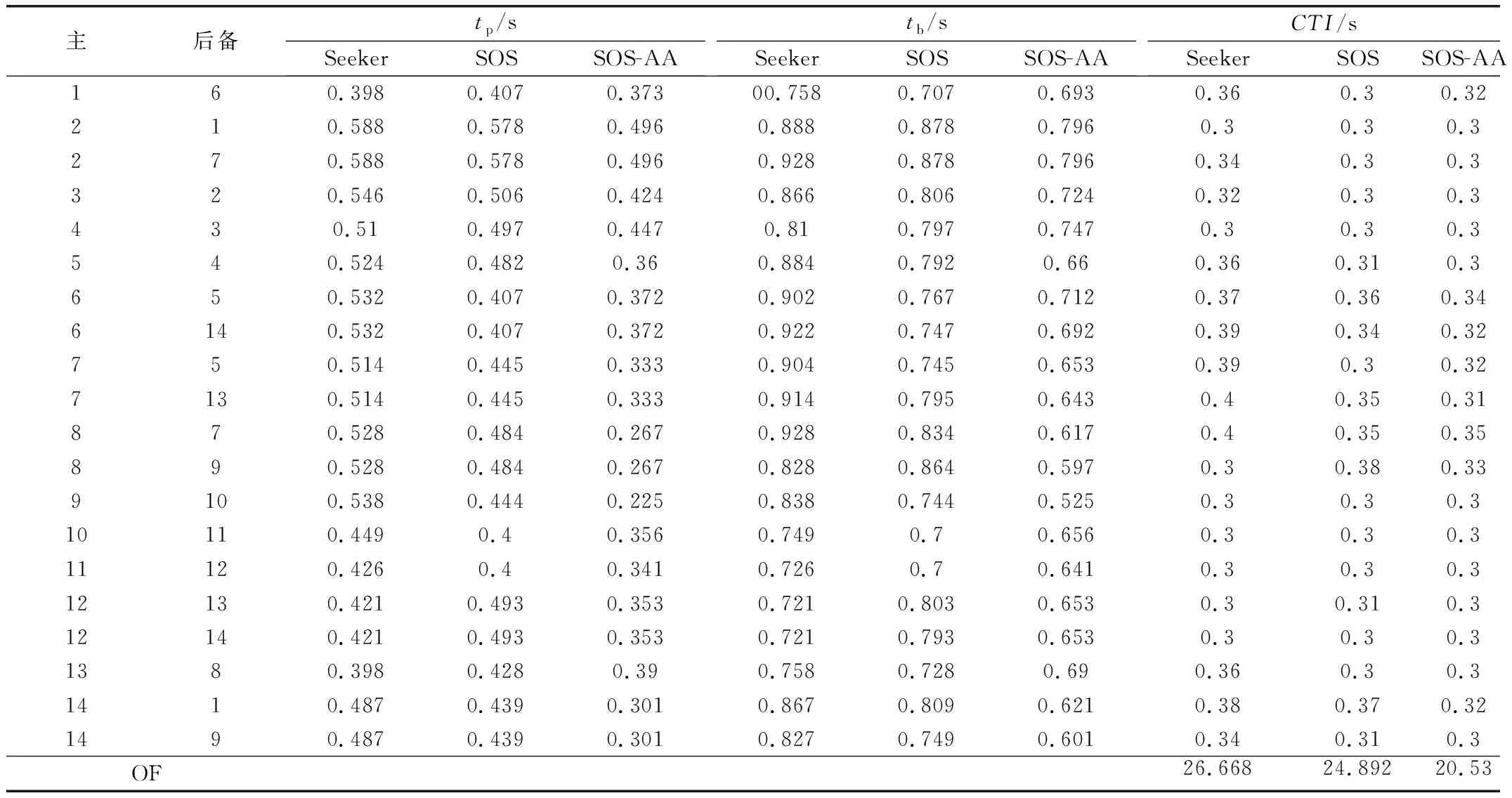
表5 IEEE 8总线系统中主/后备保护动作时间

注：tp表示主保护动作时间，tb表示后备保护动作时间。

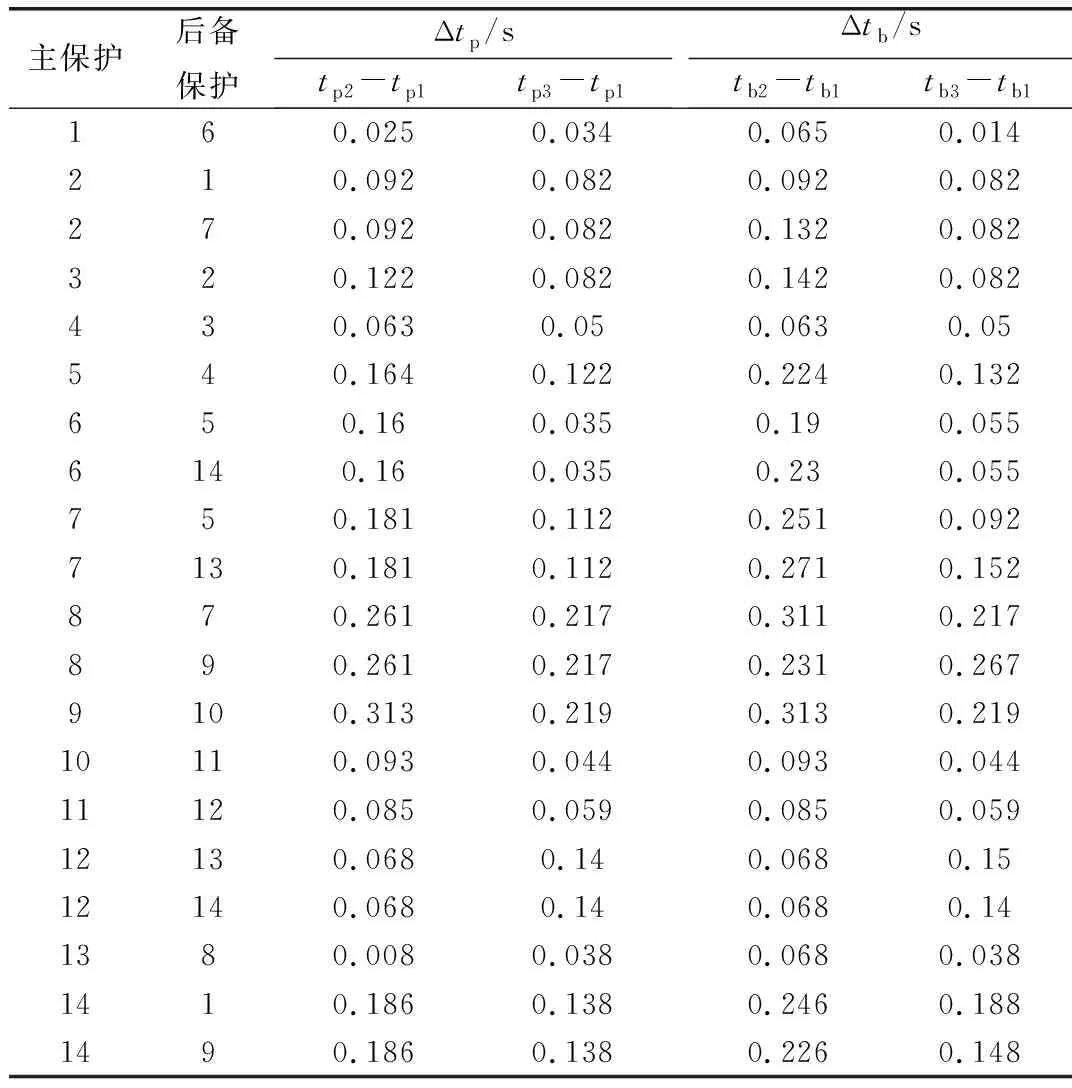
表6 基于Seeker算法、SOS算法和SOS-AA算法的保护动作时间差(8总线系统)

注：tpi与tbi中，i=1、2、3，其中 1、2、3分别对应SOS-AA算法、Seeker算法与SOS算法。

在IEEE 3节点系统和IEEE 8节点系统中仿真，基于SOS-AA算法所得出的优化方案比SOS算法和Seeker都具有更优的设定值TDS和Ip，同时减小主保护和后备保护时间，得到更优的目标函数。

4 结束语

将反时限过电流保护的协调配合问题转变成含有多个约束条件的优化问题，在SOS算法的基础上，对有利因子BF1和BF2进行了自适应改进，用改进后的SOS-AA算法来整定计算，并且和Seeker算法及SOS算法的整定结果进行了对比分析。仿真结果表明，SOS-AA算法能克服解陷入局部最优，提高收敛速度和计算精度。基于SOS-AA算法的整定结果优于Seeker算法及SOS算法的整定结果，能够提高保护的速动性。