基于Nuttall窗三谱线插值的介损角测量方法*

李媛，王海云

(新疆大学 电气工程学院，乌鲁木齐 830047)

0 引 言

在电力系统中，绝缘状况关系到电力设备的安全运行[1]，尤其对于高压设备，大多损坏都是由绝缘损坏造成的[2]。介质损耗(简称介损)是衡量电容型设备绝缘状况的一个重要指标[3]，对介质损失角进行精确监测与计算，为电气设备故障诊断提供可靠依据，准确监测电容设备绝缘情况为电力系统安全稳定运行提供重要保障。

对于介损角测量，目前主要有硬件法和数字测量，硬件法容易受外界条件干扰，容易造成误差。数字测量应用最广泛的是谐波分析方法。通过谐波分析方法得到电压和电流基波相位值，计算出电压电流两者的基波相位差的余角即为介损角。基于FFT分析的谐波方法因其方便性得到广泛应用。因为电网频率具有波动，容易造成非同步采样，产生频谱效应和栅栏效应会给电压电流参数的分析结果带来误差，从而影响介损角测量精度。通过加窗插值能够抑制频谱泄露和减少栅栏效应，从而提高介损分析精度。文献[4]提出基于Hanning窗FFT介损测量方法。与直接采用FFT比较，介损测量结果精度有数量级的提高。文献[5]提出基于Blackman窗介损测量方法。文献[6]提出基于Kaiser窗双谱线插值介损测量方法。文献[7]提出基于Rife-vicent窗双谱线插值介损测量方法。这些方法都在一定程度上提高了介损测量精度，且窗函数旁瓣性能越好，测量精度越高。为改善窗函数性能，一系列基于卷积窗函数介损测量方法被相继提出。如Hanning卷积窗[8]，三角形自卷积窗[9]，和Blackman自卷积窗[10]。这些算法提高介损测量精度，但卷积窗的频谱校正公式计算繁琐。Nuttall窗具有良好的旁瓣特性，在谐波分析中计算各参数有较高的计算精度。文献[11]将基于Nuttall窗双谱线插值法用于介损分析，测量误差为1.8e-4。文献[12]提出加Nuttall窗五点变换法，较双谱线插值法计算精度有所提高，但是需要进行离散频谱重组，计算繁琐。文献[13]将基于Nuttall窗三谱线插值法应用谐波参数分析，比基于双谱线插值法具有更高精度,三谱线插值法具有更高的精度。

为进一步提高介损测量精度，提出基于Nuttall窗三谱线插值介损测量方法。在频率波动、谐波比例变化情况下，在MATLAB中进行仿真实验。对比分析所提方法、加Nuttall窗结合双谱线插值法和加三角形自卷积窗插值法这3种介质损失角计算方法的计算结果。同时分析在白噪音存在和采样点数变化情况下所提算法测量介损时的误差情况。

1 介损测量原理

电介损质原理图如图1所示。

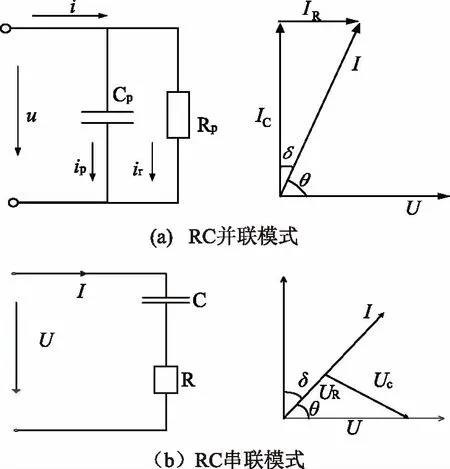
图1 电介质RC并联联/串联等值电路

电介质等效电路可以由RC并联模式和RC串联模式两种来等效[14]，图1(a)为并联等效电路和向量图，图1(b)为电介质等值电路变换串联模型与向量图。对于并联模式，其中θ为通过电介质的电流与所加电压间的相位角，即电路的功率因数角，δ为φ的余角，称之为介质损耗角。如图1(a)所示，由向量图可得介损计算公式：

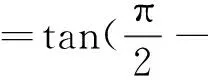
(1)

同理推导出对于串联模式：

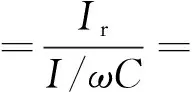
(2)

2 基于Nuttall窗三谱线插值法介损测量

2.1 Nuttall窗函数

Nuttall窗是一种余弦组合窗，它的时域表达式为：

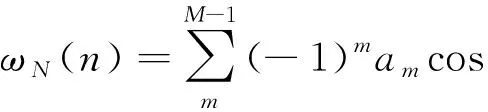
(3)

式中M为窗函数的项数；n=1，2，3…N-1;am为系数且满足约束条件：

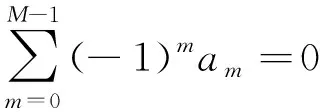
(4)

根据am的不同，Nuttall窗函数具有不同的特性，表1列出几种不同类型的Nuttall窗函数系数。

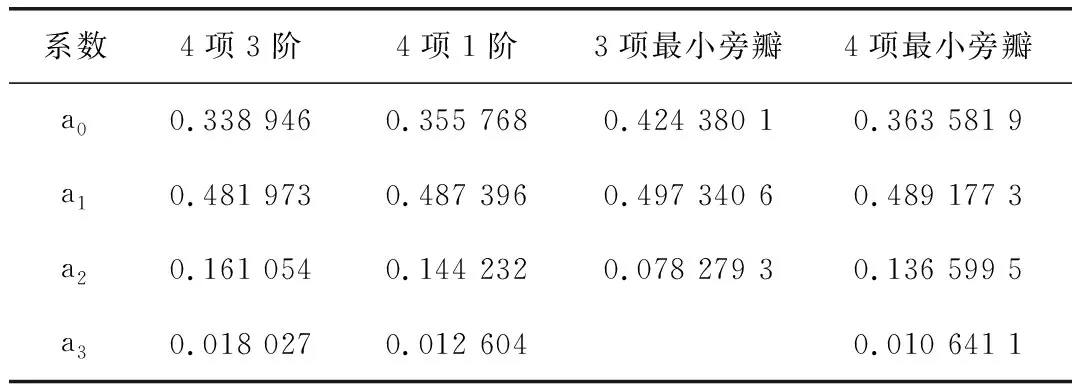
表1 Nuttall窗系数

Nuttall窗函数频谱图如图2所示。

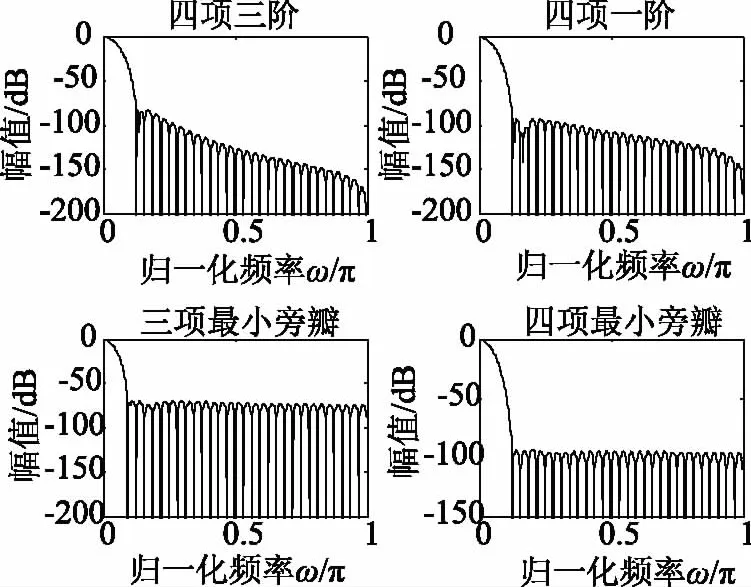
图2 Nuttall窗的幅频响应对比图

由幅频特性图可知，四项三阶的最大旁瓣峰值为-82.6 dB，旁瓣衰减速率为30 dB/oct。频谱特性最为理想，因此选用四项三阶Nuttall窗函数。

2.2 基于Nuttall窗的三谱线插值法

以单个信号为例x(t)以采样频率fs均匀采样得到离散时间信号如公式(5)所示：

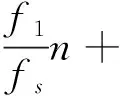
(5)

所加余弦窗函数的表达式：

(6)

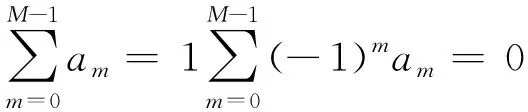
xw(n)=x(n)·w(n)

(7)

进行离散傅里叶变换为：

(8)

式中Δf=fs/N。

(9)

W(k)为窗函数DFT表达式：

(10)

所以x(n)的DFT表达式为：

(11)

如果是同步采样，k=f1/Δf为整数，因为电网的波动性，k往往不是一个整数，为了提高准确度，采用文献[15]所提出的三谱线插值法来修正。该插值法利用谐波频点附近的三根离散谱线幅值来确定谐波谱线的准确位置，充分利用了频谱信息。较单谱线插值法和双谱线插值法能得到更准确的谐波谱线位置，提高谐波分析精度。具体过程如下，选用峰值频点附近三根信息量大的谱线y1，y2，y3用于修正，ε表示偏差。

y1=X(kα-1),y2=X(kα),y3=X(ka+1)

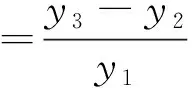
(12)

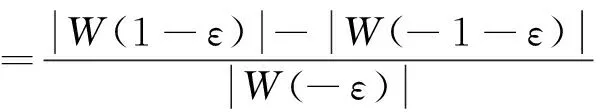
(13)

由多项式拟合得到与δ的关系式，由δ=α-1(ε)求得δ，由此可以得到幅值、频率和相位的修正公式：

f=kΔf=(kα+ε)Δf

(14)

(15)

φ=arg[X(ka)]+π/2-επ

(16)

式(14)可以写成A=N-1(y1+2y2+y3)ν(ε)形式。将4项三阶Nuttall窗系数带入式(10)，将所得表达式代入式(13)，通过多项式拟合可以推导出：

α=1.014 677 93β-0.085 167 55β3+

0.014 834 90β5-0.002 888 39β7

(17)

β=1.724 338 592+0.430 782 702α2+

0.057 559 982α4+0.005 698 372α6

(18)

2.3 基于Nuttall窗介损测量方法

对电压电流信号加窗处理进行FFT分析，得到频谱附近三根离散谱线，由公式(16)可以求得电压基波相位φu0和电流基波相位φi0。则可以得到介损角δ的计算公式：

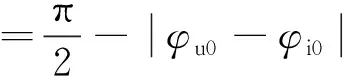
(19)

基于Nuttall窗的三谱线插值介损角测量过程如图3所示。

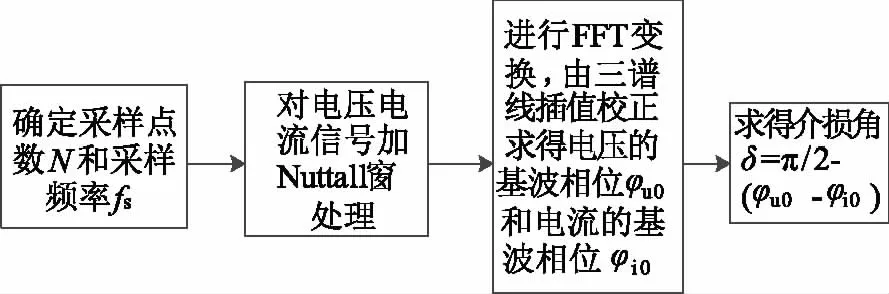
图3 介损角测量流程图

3 MATLAB仿真分析

采用文献[10]中的仿真电路和文献 [16]中的电压模型。本节采用串联等效电路等效容性设备，电压信号表达式为：

u(t)=220[sin(2πf0t+π/3)+

1.088%×sin(2π×3f0t+π/4)+

0.611%×sin(2π×5f0t+π/6)]

(20)

其中C=519.02 pF，R=22.67 kΩ。f0=50 Hz时，δ=0.004 209。为验证该算法的准确性和有效性，在基波频率波动，谐波含量变化，白噪音存在和采样点数变化情况下分析介损角的测量误差。

3.1 频率波动对介损测量的影响

频率在49.8 Hz～50.2 Hz之间波动，将基于Nuttll的双谱线法，基于Nuttall窗三谱线法以及文献[16]所提的基于三角形自卷积窗插值法用于测量δ，并将计算结果进行对比，采样频率为3 200 Hz，采样点数为512。绝对误差如图4所示。

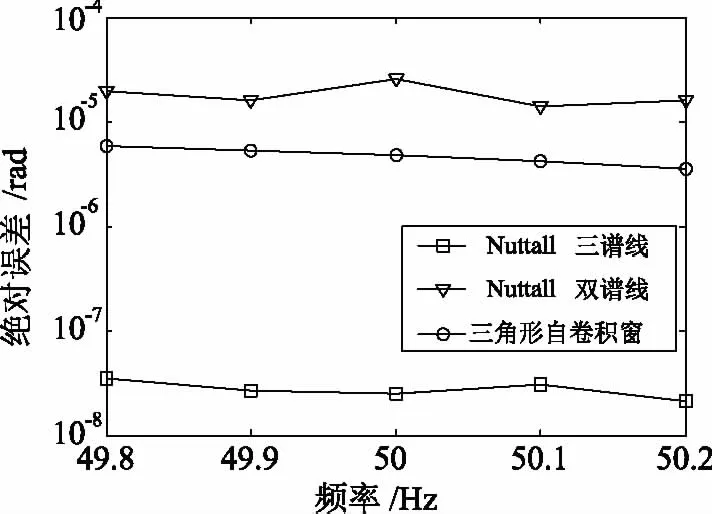
图4 频率波动对介损测量影响图

由图4可以看出，在相同条件下，所提算法误差都小于3.58×10-8，与基于Nuttall窗双谱线插值介损测量算法精度要高3个数量级，比三角形插值法要高1个数量级。且随着频率波动，对测量精度变化不大。说明在频率波动的情况下，所提算法能克服频率波动影响，具有有较高的精确度。

3.2 谐波分量对介损测量的影响

电压、电流谐波信号中三次谐波占比重大，三次谐波与基波的比值在0～8%之间变化，基波频率为50.2 Hz，测量的误差如图5所示。

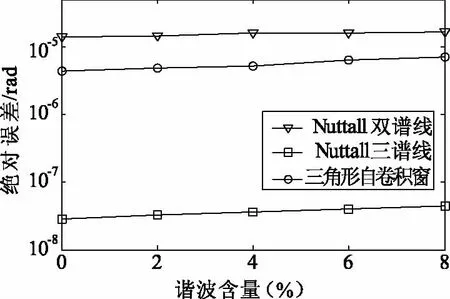
图5 3次谐波含量变化对介损测量影响

由图4可知，当三次谐波含量变化时，所提算法均测量误差小于4.8×10-8，与双谱线相比提高3个数量级。比三角形自卷积窗精度高2个数量级。在谐波变化情况下，所提算法仍然具有较高的精确度。

3.3 白噪音对介损角测量影响

在实际电网中，噪音是不可忽视的，噪音会对谐波分析产生影响，从而影响δ的测量准确度。在信号加上信躁比不同的白噪音，分析在白噪音存在的情况下该算法对δ测量准确度。噪音具有随机性，通过100次测量取平均值来降低测量误差，误差结果如图6所示。

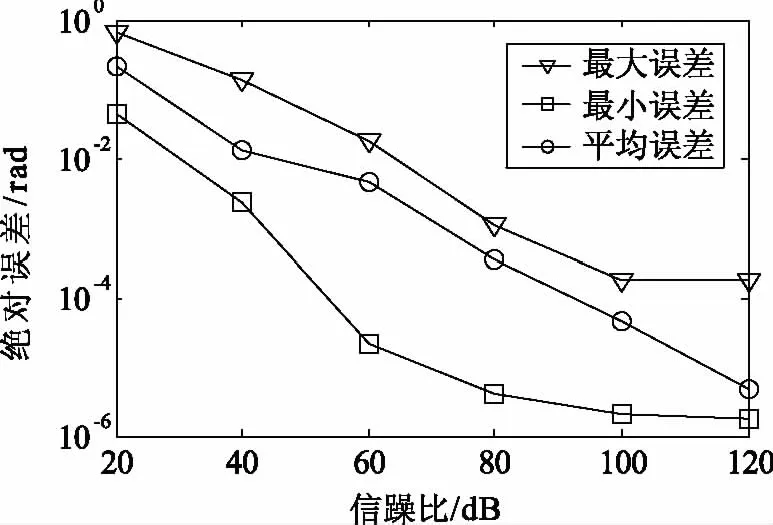
图6 白噪音下介损角测量误差图

由图6可知，信噪比不同情况下，介损角的测量精度不同。信噪比小，噪音强度大，测量误差大。当信噪比大于60 dB时，均值误差小于4.6×10-3。同时，由图6可知多次测量取平均值能降低介损测量误差。白噪音的存在，会降低测量精度，因此采取一定的去噪措施能提高介损角的测量精度。

3.4 采样点数对介损角测量的影响

固定频率为3 200 Hz，采样点数分别取为256，512，1 024，2 048。测量介损角，误差分析如图7所示。

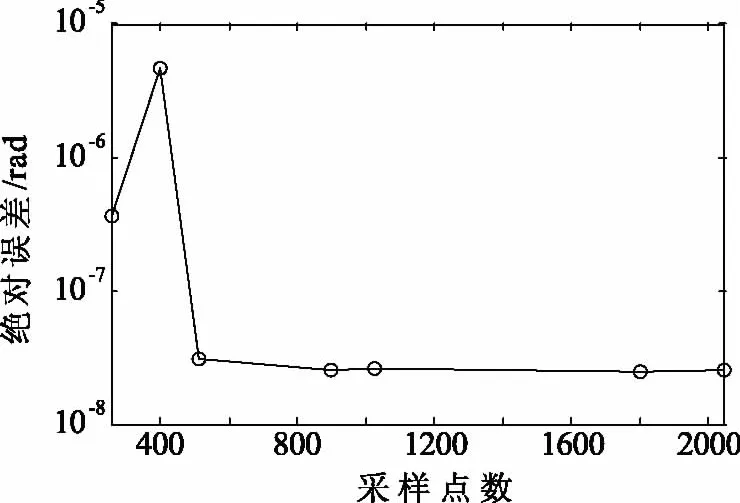
图7 采样点数对介损角测量的影响

采样点数对介损测量误差都小于1.57e-7,在点数增加，精度变化不大，采样点数在512时，测量绝对误差为3.06×10-8，已经具有较高精确度。当频率一定时，选择合适的点数即可得到较高的计算精度，同时能减少计算量。

由以上所有分析结果可知，所提算法测量介损角时，在非同步采样情况下均有较高的精度。频率波动，谐波含量变化，采样点数变化测量精度均比较稳定。在白噪音存在的情况下误差稍有增大，因此，需要采取措施减少白噪音对测量的干扰。

4 结束语

研究了Nuttall窗的频谱特性。结合三谱线插值法，将基于Nuttall窗三谱线插值法应用于介质损失角测量。在频率波动，谐波含量变化，白噪音存在，采样点数变化的况下分析介质损耗角的测量准确度。

仿真实验结果表明：Nuttall窗具有良好旁瓣性，能减少频谱泄露给介损测量的影响，三谱线插值法较双谱线具有更高的计算精度。该算法能克服频率波动和谐波含量带来的影响。在白噪音存在的情况下能仍有较高的计算精度。且该算法易编程实现，可满足电容型设备介损角在线监测的要求。