一种基于瞬时无功功率的电能计量方法

李贺龙，郑智斌，刘建志，赵进全

(1. 中国电力科学研究院，北京 100192； 2. 西安交通大学 电气工程学院，西安 710049)

0 引 言

近年来，随着电力电子技术和新能源技术的快速发展，大量的非线性电源和负载接入电网，导致电网电能质量问题日趋严重，信号波形严重畸变，三相非正弦不平衡现象也越来越严重，传统的三相平衡电能计量理论也将出现较大的电能误差[1-4]。

目前大多数的电能计量方法都是针对工频电路设计的，因此非正弦电路会对其计量结果造成很大影响。非正弦不平衡情况下的电能计量问题已经引起越来越多的重视。国内外学者也先后提出均方根法、傅氏法等算法[5]。虽然这几种方法都能在某些角度满足要求，但仍然存在着很多不足。均方根法是先计算视在功率和有功功率，再计算无功功率[6]。该方法计算简单，但计算的无功功率为Fryze时域定义下的无功功率而不是更广泛使用的Budeanu频域定义下的无功功率，而且该方法不能避免不同次谐波产生的功率正负抵消的现象[7]。傅氏算法的思路来自傅里叶展开，是通过将电压电流信号进行傅里叶级数展开后得到电压电流信号的Budeanu频域表达式，进而可以分别求出各次的谐波的有功功率和无功功率。该方法精度高，并且可以分别计量各次谐波的有功功率和无功功率，但计算量大，而且在实际应用时不能计算出全部的谐波功率，计量误差大[8]。

针对目前电能计量方法存在的问题，提出一种针对三相三线制系统的电能计量方法。该方法通过改变瞬时无功功率中p-q坐标系的旋转方向和旋转速度，分别提取三相电压电流信号中的正负序分量，进而求得正负序功率。最后通过功率转换求得三相三线制系统下的有功功率和无功功率。该方法可以计量有功功率及Budeanu频域下的无功功率，可以实现功率的正反向计量，避免了不同次谐波功率相互抵消的不合理现象，计算量小，计算精度高。最后通过Matlab仿真对该方法进行验证。

1 改进瞬时无功功率理论的电能计量技术

1.1 电压电流正负序各次谐波分量的提取

对于非正弦不平衡三相三线制系统，三相电流可以写成[7-8]：

(1)

式中I为电流的有效值；φ为电流初相角，下标中的1为正序分量，2为负序分量,n为n次谐波。

将三相电流经Clark变换转换至α-β两相正交的坐标系。

(2)

再经过Park变换将其变换到正向旋转的p-q坐标系下，如图1所示。

图1 α-β坐标系和正向旋转的p-q坐标系

(3)

可知，ip、iq中的直流分量是由正序基波电流产生，通过滤波便可以得到：

(4)

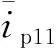
同理，改变坐标系旋转方向，使p-q坐标系反向以角速度ω旋转，如图2所示，则有：

(5)

图2 α-β坐标系和反向旋转的p-q坐标系

可知，ip、iq中的直流分量是由负序基波电流产生的，可得：

(6)

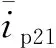
(7)

(8)

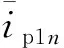
同理，对三相电压经过变换得到p、q坐标轴正负序电压的各次谐波分量:

(9)

(10)

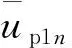
1.2 功率计算

根据电路理论，n次谐波正序有功功率为：

P1n=U1nI1ncos(ψ1n-φ1n)=U1ncos(ψ1n)I1ncos(φ1n)+

(11)

同理，可以求得n次谐波的正序无功功率、负序有功功率及负序无功功率分别为：

(12)

(13)

(14)

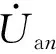
=3P1n+3P2n

(15)

同理，可得n次谐波无功功率为：

Qn=3Q1n+3Q2n

(16)

则三相三线制系统中总有功功率和无功功率分别为：

(17)

(18)

通过式(15)和式(16)就可以得到任一次谐波的有功功率和无功功率，从而防止了不同频次谐波正负抵消产生的不合理现象。

2 仿真验证

利用Matlab软件搭建三相非正弦不平衡系统，各相的谐波电压和电流如表1～表3所示。电压、电流中均含有3、5、7、9次谐波。

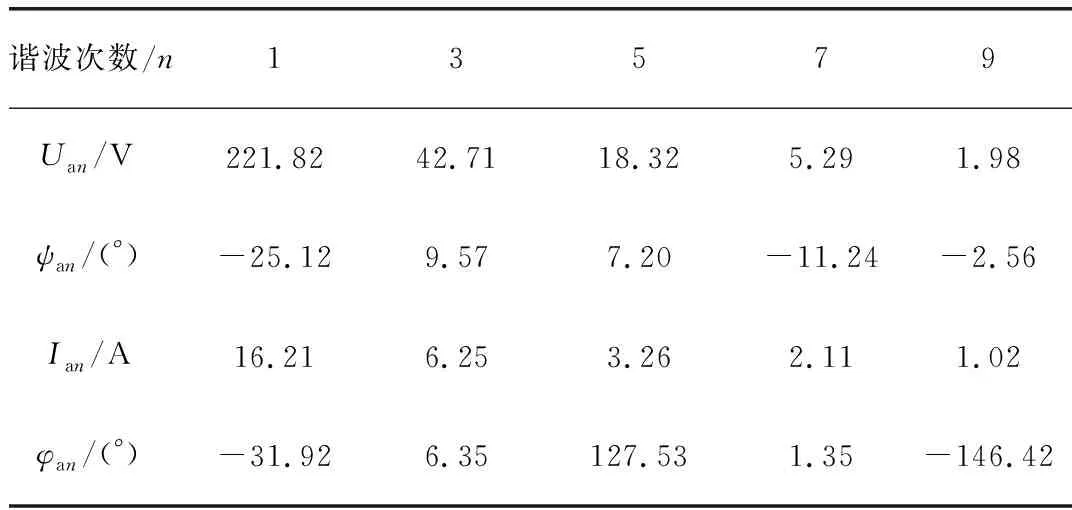
表1 A相谐波电压和谐波电流

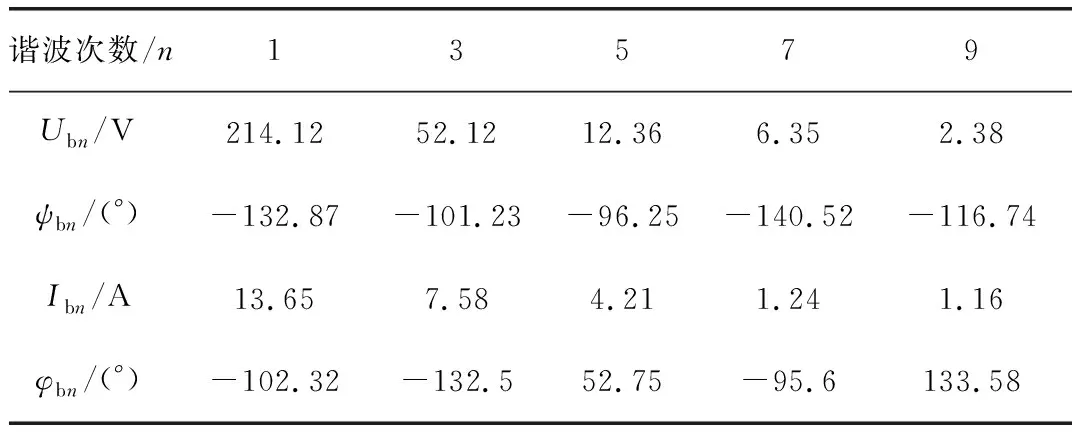
表2 B相谐波电压和谐波电流

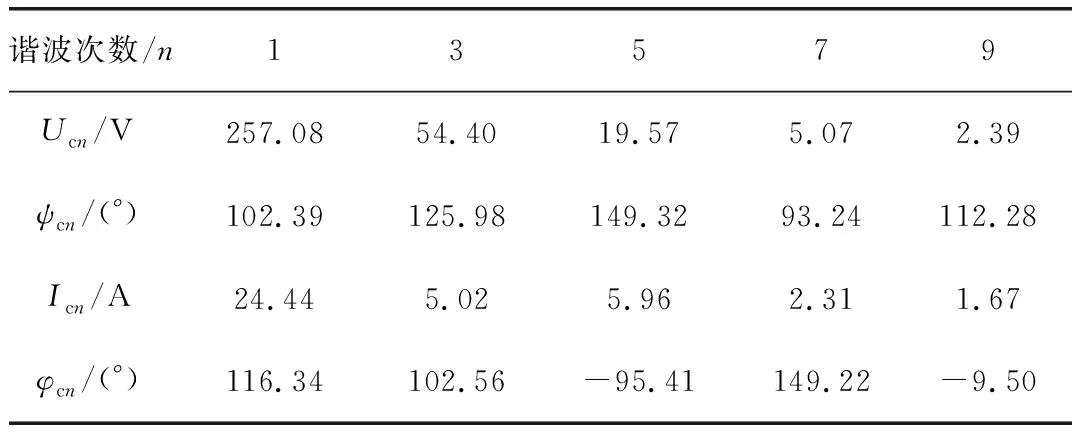
表3 C相谐波电压和谐波电流

使用文中方法对三相非正弦不平衡电路进行计算，并与Budeanu下的功率进行比较，结果如表4、表5所示。

由表4、表5可以看出，文中方法可以分别计量各次谐波的有功功率和无功功率的大小和方向，防止不同频次谐波功率互相抵消的不合理现象。由文献[6]可知文中方法具有很高精度。方法误差的主要来源是滤波器[10]，提高滤波器的滤波性能可以进一步降低计量误差。

表4 实验结果

3 结束语

提出的基于瞬时无功功率的电能计量方法，是通过改变广义瞬时无功功率理论中p-q坐标系的旋转方向和速度，从而将电压电流中的各次谐波的正负序分量提取出来，进而计算系统功率。该方法具有计算简单、计算量小的优点，并且可以分别得到各次谐波的有功功率和无功功率，防止了不同频次谐波功率抵消的不合理现象,最后通过Matlab仿真验证看该方法的准确性。