高磁导率比双铁芯电流互感器原理和误差性能研究*

熊魁，岳长喜，李登云，朱凯，李智成

(中国电力科学研究院，武汉 430074)

0 引 言

气隙电流互感器以其抗饱和能力强的特点最早由原苏联的研究者用于电力系统，但由于气隙电流互感器的误差测量准确度较低，目前气隙电流互感器主要应用在继电保护方面，文献[1]构建了铁心开气隙电流互感器的等值电路模型,分析了气隙对CT性能的影响。文献[2]利用 J-A 模型建立了铁心开气隙互感器的仿真模型,分析了不同气隙大小对于电流互感器的暂态特性的影响。气隙互感器具有很强的抗饱和能力，可以解决传统互感器在直流分量下无法准确测量的问题，但气隙电流互感器在正弦交流下误差较大，或者需要增加有源的电子元件进行补偿，这些限制了其广泛应用[3-10]。

提出一种结合气隙电流互感器和普通电流互感器的双铁芯电流互感器，其能在正弦交流和直流分量下计量交流电能，分析其抗直流性能与互感器参数的函数关系，建立双铁芯电流互感器的数学模型并阐述其误差性能，通过实验验证该双铁芯电流互感器的有效性，最终给出双铁芯电流互感器的基本计量特性和相应结论。

1 直流下气隙电流互感器抗饱和能力的理论分析

一般气隙电流互感器的铁芯截面上有一个或两个完整的气隙，在这种情况下每个气隙中的磁密Ba与铁芯中非气隙部分的磁密Bi是相等的，即Ba=Bi，根据文献[1]气隙互感器的励磁电感L0可看作是铁心非气隙部分电感Li与气隙电感La的并联，即：

(1)

式中N2为二次绕组的匝数；μi为铁芯非气隙部分的磁导率；μa为气隙的磁导率；S为铁芯的截面积；li为铁芯非气隙部分的平均磁路长度；la为铁芯气隙的平均磁路长度。

对于冷轧硅钢片气隙铁芯一般磁路长度la>0.001li，磁导率μi=(10 000～50 000)μa，所以在直流分量使铁芯饱和前有Li>>La，则推出：

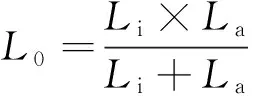
(2)

式中 气隙电感La的值可以看作常量C，等效电路中总的励磁电感相当于铁芯非气隙部分电感与气隙电感的并联，在铁芯饱和前其值近似于恒定的气隙电感，因此原S型B—H磁化曲线饱和点前的曲线部分将会线性化。根据文献[2]结论最大磁密Bmax值几乎不变，对于同一个铁芯其气隙越大，磁导率越小，磁化曲线线性部分斜率越小，且相对应的磁场强度Hmax越大，铁芯越难以饱和。根据上述分析可计算气隙电流互感器所能承受的最大直流电流，由于直流分量通过一次绕组时不能传递到二次侧，其全部用来励磁，直流含量大于3%时有：

IDN1>>I0N1

(3)

式中N1为一次绕组的匝数；ID为直流电流；I0为交流励磁电流。

因此，可以认为总的励磁电流都由直流分量提供：

IDN1=Hl0

(4)

式中H为铁芯磁场强度；l0为气隙铁芯的平均磁路长度。

据式(1)、式(2)，可计算气隙铁芯的等效磁导率μ0为：

(5)

且有：

(6)

式中B为铁芯磁密。根据铁芯材料的饱和磁密Bs，联立式(4)～式(6)，则有：

(7)

因此，气隙电流互感器所承受最大直流电流与铁芯饱和磁密、气隙长度和一次匝数有关。为了验证上述分析的有效性，对不同气隙大小(0.1 mm～0.6 mm)的气隙铁芯和普通电流互感器的超微晶铁芯的磁性参数进行试验测试，得到其磁化曲线见图1，损耗角曲线见图2。

根据图1分析铁芯气隙大小和其能承受最大磁场强度之间的关系，铁芯气隙越大，其磁化曲线斜率越小，即气隙铁芯的饱和磁场强度和气隙大小呈正相关，因此可以通过调整铁芯气隙大小来改变其抗直流能力。

图1 不同气隙大小铁芯和超微晶铁芯的磁化曲线

图2 不同气隙大小铁芯和超微晶铁芯的损耗角曲线

由于气隙铁芯等效磁导率μ0相对完整铁芯磁导率μi很小，则同样结构参数的气隙电流互感器在正弦交流下的复数误差ε0将大于普通电流互感器的误差。同时如图2所示，由于气隙铁芯损耗角ψ很小(1°～4°)，假设负载为纯阻性即阻抗角为0，根据相位差δ和比值差f的关系，可得δ/f=εcosψ/εsinψ=cotψ>>1，即气隙电流互感器在不进行补偿的情况下相位差远大于比值差。综上所述，可以得到以下三点结论：

(1)气隙电流互感器可以根据直流分量的大小来调整气隙的大小，以保证互感器不会出现饱和现象；

(2)在直流含量很小或没有直流时，气隙电流互感器误差特别是相位差比普通电流互感器要大，这限制了气隙电流互感器的应用；

(3)随着直流含量不断增加，普通电流互感器进入深度饱和状态，磁导率不断下降，同时损耗角快速减小，导致其比值差往负偏，相位差往正偏，且相位差变化相对于比值差大。

2 双铁芯电流互感器理论基础和等效模型

为了在交流和直流分量下同时保证电流互感器的误差测量性能，综合普通电流互感器和气隙电流互感器的特点，采用如图3所示结构组成双铁芯电流互感器，其中右边的是普通电流互感器T1，左边是气隙电流互感器T2。其中普通电流互感器主要保证在正弦交流下的测量精度。气隙电流互感器主要作用是保证在较大直流分量下的测量准确度。

图3 双铁芯电流互感器

假设两个互感器基本参数一致，根据磁势平衡方程有：

(8)

式中I01为普通电流互感器T1中的励磁电流；I02为气隙电流互感器T2中的励磁电流，由于T1和T2头尾串联，使得两个互感器一次和二次电流相等，根据式(8)可以看出两互感器励磁电流相同，即：

I01=I02=I0

(9)

由I0N1=HL，互感器其他参数相等，可以推出两互感器磁场强度H相同，即：

H1=H2

(10)

根据互感器电路和磁路关系有：

(11)

式中k为铁芯的叠片系数；Z02为二次总阻抗;Zm为励磁阻抗。

联立式(6)、式(11)可得：

(12)

根据式(8)、式(9)及图3可以得出双铁芯电流互感器的等效电路如图4所示，通过化简得到标准的等效电路如图5所示。

图4 初始的双铁芯电流互感器等效电路

图5 标准的双铁芯电流互感器等效电路

根据标准的等效电路，在其他参数相同情况下，由式(11)、式(12)和互感器磁导率μ，可推出互感器T1和互感器T2励磁阻抗Zm及感应电势E之间的关系。互感器T1在接近饱和点以前其磁导率μ1远远大于互感器T2的磁导率μ2，使得励磁阻抗Zm1>>Zm2且感应电势E21>>E22，则双铁芯电流互感器总的二次感应电势E2基本由普通互感器T1承担，根据误差公式可以得出两互感器组成双铁芯电流互感器的误差为：

(13)

其误差值与互感器T1的误差十分接近，不过由于Z22的引入使其比互感器T1误差略大，而双铁芯电流互感器误差接近互感器T1的误差程度与励磁阻抗Zm1大于Zm2的程度相关。

图6 超微晶铁芯和气隙铁芯磁化曲线

3 试验验证

采用上述原理研制一台500 A/5 A的双铁芯电流互感器样机，其一次绕组N1=1匝，采用穿心的方式穿过铁芯，二次绕组N2=100匝，均匀绕制。作为比对的普通电流互感器为超微晶铁芯、气隙电流互感器为冷轧硅钢片铁芯开气隙，其他参数与三者一样。在实验室对普通电流互感器、气隙电流互感器和双铁芯电流互感器分别在正弦交流和3%～10%直流分量下进行误差试验，其中测量装置通过采用Labview程序、高速双通道数字采集卡构建了一种宽频高精度电流比例测量装置[11]，误差测试结果见表1～表3。

通过表1～表3可以看出，双铁芯电流互感器在正弦交流下比值差小于0.1%，相位差小于6′，相当于普通电流互感器在正弦交流下的误差；在直流含量为3%～10%的范围内其比值差小于0.2%，相位差小于110′，比普通电流互感器在同样直流分量下的误差小很多。再以100%额定电流下正弦交流和不同直流分量的误差为例进行说明，如图7和图8所示，在直流含量为0%时，双铁芯电流互感器的比值差和相位差接近普通电流互感器的比值差和相位差，随着直流含量增加，双铁芯电流互感器的比值差和相位差趋近于气隙电流互感器的比值差和相位差，可以看出实测误差与之前的理论推导分析一致。因此，由于双铁芯电流互感器的上述误差特性使其具有较大的应用潜力。

表1 普通电流互感器误差

表2 气隙电流互感器误差

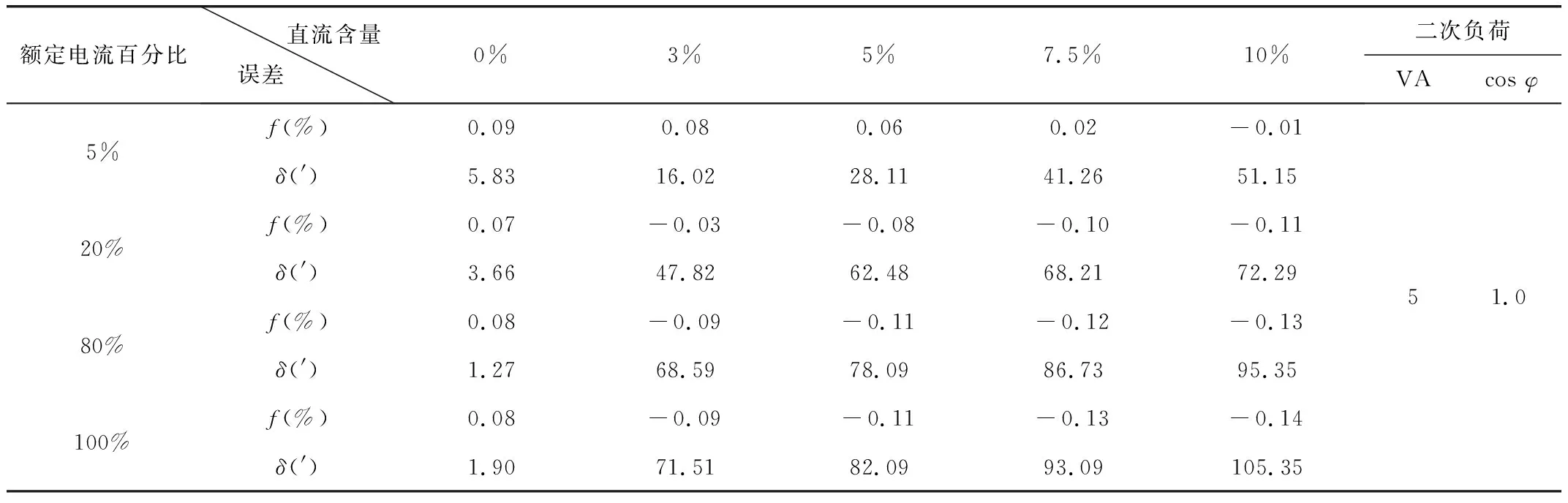
表3 双铁芯电流互感器误差

图7 100%额定电流下各互感器在不同直流分量的比值差

4 结束语

研究了气隙电流互感器的抗饱和能力，并基于双铁芯电流互感器的结构和电路原理，得到了相应的T型等效电路模型，推导了双铁芯电流互感器器的误差公式，并进行了误差校验，可到如下结论：

图8 100%额定电流下各互感器在不同直流分量的相位差

(1)气隙电流互感器能承受最大直流电流与铁芯的饱和磁密、气隙长度和一次匝数有关，一般通过改变气隙的大小可以调整其抗饱和能力，但其在正弦交流下的误差比普通电流互感器要大;

(2)双铁芯电流互感器除了具备气隙电流互感器的抗饱和能力外，在正弦交流下有普通电流互感器的准确度等级，在存在使普通电流互感器饱和的直流下也具有一定的测量准确度;

(3)通过误差试验测试，所研制的双铁芯电流互感器样机在正弦交流下比值差小于0.1%，相位差小于6′，在直流含量3%～10%下比值差小于0.2%，相位差小于110′。