基于改进马氏距离的空压机健康状态评估*

张红飞，夏霜，程志友，李小静

(1.国家电网安徽省电力公司培训中心，合肥 230039； 2. 教育部电能质量研究中心，合肥 230039)

0 引 言

电力设备是电力系统中重要的组成部分，其运行状况的好坏对整个电网系统的安全与稳定运行至关重要[1]。除了在电力设备的设计和制造过程中提高其可靠性外，更重要的是在电力设备的运行过程中，实时地评估其健康状态，进行科学的故障诊断，预测性能发展趋势，对设备的退化及时发出警报，优化设备维护计划，降低生产损失。由于电力设备是一个复杂系统，早期退化的征兆不明显，其状态评估是一项复杂而艰巨的工作，所以有效的健康状态评估方法是此类研究的关键[2-3]。

在现有的研究中，针对电力设备故障诊断的研究比较多，而对电力设备或系统的状态预测研究相对较少，相关的研究比如文献[4]的层次分析法，通过结合专家经验，对各层结构中的各状态参量进行权重分析，其一定程度上能有效地评估电力变压器的运行状态，但是此方法指标统计量过大且难以确定其权重。刘博元等提出的基于大数据的复杂生产线的健康度实时评估方法[5]，以生产线系统运行中的实时大数据(流数据)为基础，综合利用关联规则和评估精度进行相关性挖掘，再引入信息熵原理量化关联规则最终合成健康度，这种方法从大数据角度分析和量化健康度，具有一定的通用性和参考意义，但是过程过于复杂。文献[6]提出了基于模糊理论的状态评估方法，其建立考虑高压断路器运行机理的递阶层次评估模型，并引入了点灰度描述模糊关系，通过建立黑色模糊判别矩阵，判别了其运行状态。实际算例表明所提模型能有效地评估高压断路器的状态，但是如何更加合理地确定权重集有待进一步的研究和完善。

马氏距离(Mahalanobis Distance，MD)[7-8]是由印度统计学家P. C. Mahalanobis提出的一种距离度量方法，通过计算两个样本集之间的协方差距离来度量两个样本之间的偏离度，其值越大表明两个样本之间的偏离度越大，其与欧氏距离、切比雪夫距离等方法一样，均可以使多元变量问题转化为单一变量问题，而相对于其他两种距离度量方法，马氏距离对多元变量的变化敏感，并且是尺度无关的，即不受量纲的影响，所以更能体现各状态特征间的关系，降低相关性干扰[9]。设备发生故障必然会伴随着性能参数偏离正常波动范围，利用马氏距离可以检测出这些异常点。目前马氏距离法已经是电力设备健康状态评估领域的一种重要方法[10-11]。

将马氏距离法引入到电力设备健康状态评估中，并根据此设备的特性对马氏距离法做出了改进。单个或少许几个改进马氏距离偏离正常阈值，可能是劣化故障，也有可能是由于环境扰动造成的瞬时故障。为了研究设备的性能参数存在的某种趋势，只有考虑设备运行过程中的历史数据信息，研究改进马氏距离历史时间序列才能很好地区分瞬时故障和劣化故障。因此结合统计学中的直方图法构建了一种新的度量指标，即退化指数，通过滑动窗口计算随着时间变化的改进马氏距离的直方图变化来检测故障类型，评估设备健康状态。

1 改进马氏距离

1.1 马氏距离

设第i个样本的第j个性能监测数据可以表示为Xij，其中i=1，2，…，n和j=1，2，…m。n表示样本的数量，m表示监测数据的维数。列出矩阵Xn×m=[X1,X2,…,Xm]，其中Xi表示n个样本的第i个性能监测数据所构成的行向量。

定义马氏距离为：

(1)

(2)

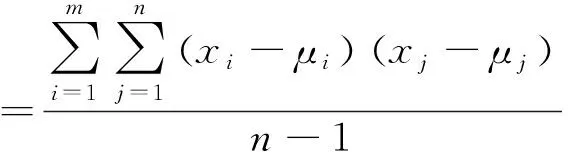
(3)

式中μ和∑分别为样本总体的均值向量和协方差矩阵。

马氏距离的缺点是其夸大了变化微小的参数的作用，微小参数除了使向量值自身产生偏移，也会导致均值向量值的改变，从而对其他各参数的马氏距离值产生偏差，影响评估的准确性[12]。

1.2 改进马氏距离

将马氏距离应用到空压机健康状态评估中并做出了改进：用空压机额定参数(额定工作情况下的一些技术数据)代替样本集的均值向量μ，显然改进后的马氏距离不受向量变化影响，是相互独立的。使用各个参数无故障时的值(比如电压、电流、有功功率等)具有实际的物理意义，比采用空压机容差范围内样本集的均值μ更适用于设备异常点的检测。因此改进马氏距离采用具有实际物理意义的标称值代替采集的样本集的均值，更能反映设备的实际运行状况。

在设备实际运行过程中，环境的瞬时扰动(如电力系统内部电能质量的扰动)也可能会导致设备某个观测点上的数值发生不规则波动，所以只有持续研究此设备的改进马氏距离时间序列，采用一定的方法分析时间序列的整体分布情况，才能更好地评估设备的健康状态。

2 退化指数的构建

2.1 最佳组距与直方图的构建

为了研究改进马氏距离时间序列，需要诸如直方图法、核估计法以及正交序列法等，来估计样本的总体分布特性。其中，直方图法由于其简单、直观、易懂等优点，是一种最为常见的密度估计和数据分析工具[13]。采用直方图法分析改进马氏距离时间序列。制作直方图需要按组距相等的原则对数据进行分组，关键点是分组数和组距的确定。如果组距选择太大，对应的分组数就会较小，制作的直方图会很平坦(过平滑)；反之，如果组距选择太小，对应的分组数较多，数据(过平滑)，两者均不能充分显示样本信息。

由于文中改进马氏距离不完全服从正态分布且具有多模态性，需用核密度估计处理此数据。实际运用中，数据具有连续性且可微性时，可选择Gaussian核函数来简化计算[14]。而Gaussian核最佳组距公式为：

(4)

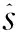
在直方图的绘制过程中，一旦确定了组距、相应的组数就确立了。组数公式为：

(5)

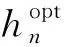
文中直方图是按0到改进马氏距离阈值以最佳组距进行分组为底边(并额外增加一个分组，用以保存超过阈值的一部分数据)，以频数(观测的改进马氏距离出现次数)为高连接起来的一系列直方形矩形图。由此可知直方图中值较小的分组代表着健康状态，而值较大的分组代表着设备偏离了健康状态。随着设备的退化，改进马氏距离较小组占的比重减小，而改进马氏距离较大组占的比重在增大。可见制作直方图来描述此时间段内改进马氏距离的频率分布状况，可以有效减少测量误差和环境扰动导致的噪声干扰。

2.2 结合滑动窗口的退化指数构建

定义直方图中单组中的观测值的数量除以总的观测值数量为频次贡献率(Frequency Contribution，FC)。文中采用滑动窗口[15-16]的方法，在时间轴上从左到右以固定时间间隔滑动窗口，计算直方图每组的频次贡献率。窗口大小的选取需根据数据采样率的大小和能否充分代表设备性能变化等多方面来考虑。每滑动一个窗口都会产生一个新的直方图。从直方图中可以看出一段时间内设备健康状态的变化，每组的频次贡献率变化趋势可以用于评估设备的健康状态，斜率增大可以认为是设备发生故障或退化的征兆。

每个时间点的退化指数(Degradation Index，DI)定义为一个时间窗内直方图中每组的频次贡献率乘以各自权重的总和。

即定义第k时刻的退化指数(DIk)为：

(6)

式中k表示时间，l=1,2,…,b,b为总组数；wl代表分配给每组的权重；fckl是k时刻第l组的频次贡献率。移动窗口则生成了相应的退化指数序列。

依次将较高的权重系数分配给较大的改进马氏距离的组，直方图中的组随着改进马氏距离的增大升序排列。瞬时发生的故障会导致较大改进马氏距离，要分配较大的权重是由于这种故障会给设备带来更大的危害以及更少的反应时间。

定义直方图每组的权重为：

(7)

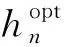
事实上，可以给较大的改进马氏距离分配相同的权重，但是会使得有些故障被忽略。而反相分配权重，会导致健康数据(较低改进马氏距离)的权重更大，使得结果难以解释。由此可见，权重的合理分配有助于更好地评估设备的健康状态。

理论上，退化指数越小代表设备健康状态越好。假设模拟数据的直方图组数为10，根据公式(7)得知，组1的权重W1=1，组10的权重W10=10，退化指数为1(所有的数据全部落在最左端的组中，其fc1=1)就代表着健康设备，10就代表设备已经退化(所有的数据全部落在最右端的组中，其fc10=1)。退化指数接近1为健康，接近10为退化。一般选取设备正常工作下退化指数最大值的95%～99.9%为阈值。在具体的工程应用中，根据设备承担风险的能力来决定合适的阈值大小。根据电力系统阈值的一般选取方法，设定最大值的98%为阈值，来评估设备的健康状态。

确立了设备正常状态数据(作为训练数据)退化指数的阈值后，设备正常运行采集的数据的信息比如均值、标准差、协方差矩阵、滑动窗口的大小、最佳组距等可用于后期测试数据的处理分析中。设备后期采集的测试数据(作为训练数据)的退化指数建立方法设备正常运行状态时的方法相似。

3 空压机的健康状态评估实例

空压机是制氧系统的关键设备，其健康状态直接影响制氧系统的安全运行。文章对某制氧厂2008年采购的一台空压机的运行状况进行评估，通过采集与空压机正常运行至关重要的电压、电流、有功功率、无功功率以及电动机的轴径向位移这五个性能参数，在线评估空压机的实时健康状态。

空压机健康状态评估流程如下：(1)监测此空压机的五个相关的性能参数；(2)构建改进马氏距离时间序列；(3)确定改进马氏距离阈值；(4)选定滑动窗口大小；(5)构建一个滑动窗口内的直方图并计算此直方图的频次贡献率；(6)移动窗口并计算相应窗口内的退化指数；(7)设定退化指数阈值，分析空压机健康状态。

采集空压机正常运行时的160组数据经处理后作为训练样本，并将其转化为改进马氏距离观测序列。根据98%的置信度要求，如图1所示，得到改进马氏距离阈值为4.696 5。

运用训练样本处理得到的样本标准方差及式(4)计算出的直方图最佳分组，得到组距为0.353 4。结合之前得到的改进马氏距离的阈值及式(5)，得到直方图最佳组数为14。以12个观测点为一个滑动窗口制作直方图，计算滑动窗口内每组的频次贡献率并根据式(6)、式(7)计算训练样本的退化指数。按照退化指数98%的置信度，计算退化指数阈值为6.778 3，如图2所示。

图1 训练样本的改进马氏距离

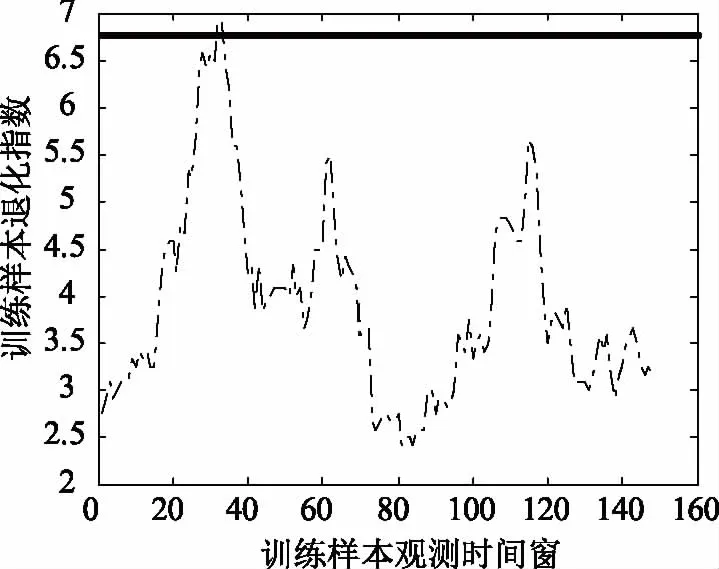
图2 训练样本的退化指数

采集空压机后期数据作为测试样本，选取其中的一段186组数据来进行说明。观测时间窗的组数和权重与训练样本数据相同，得到的改进马氏距离时间序列和退化指数分别为图3、图4所示。

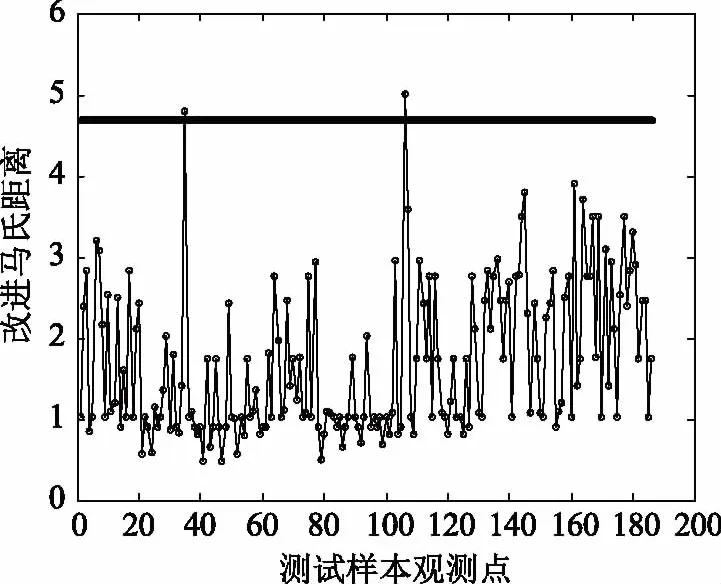
图3 测试样本的改进马氏距离

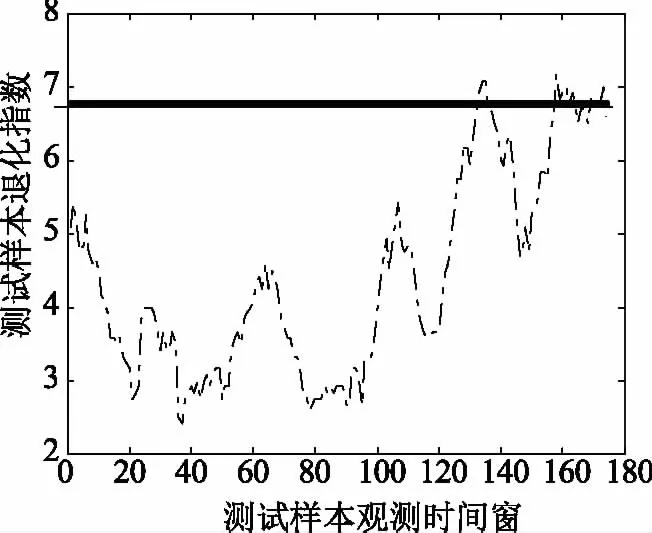
图4 测试样本的退化指数

测试样本的改进马氏距离反映设备实时性能状态，而退化指数因为参照了历史数据，可以反映设备一段时间段内的设备性能变化。采样点35的改进马氏距离超过了阈值，而相应的退化指数并没有超过阈值，观察直方图中这个点附近的改进马氏距离并不呈现一定的趋势，说明这个时刻的数值波动很可能是由于环境扰动导致的。对这个观测点及其相邻时刻的数据进行采集分析，得知该时刻制氧系统内部产生0.08 s的A相电压暂降，后又恢复正常，可见该观测点产生的异常值是由于系统的电能质量扰动问题导致的，并不是空压机设备自身健康状态的变化所致，与本论文方法分析的结果相符合。采样点35及其邻近时刻的电压、电流波形如图5所示。

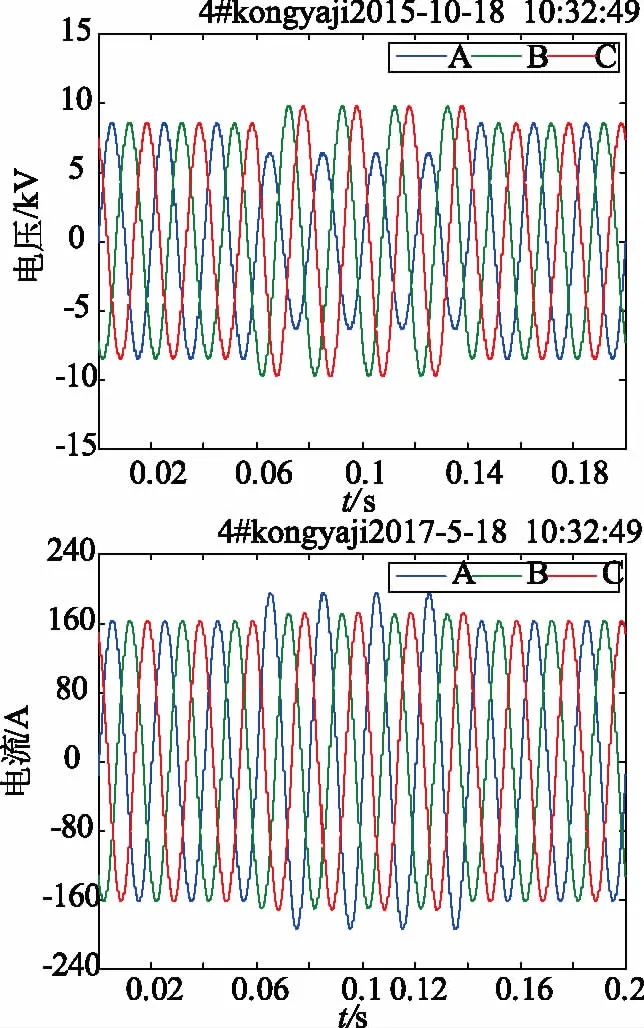
图5 采样点35及相邻时刻的电压和电流波形

采样点108组的改进马氏距离超过了阈值，在此之后直方图中第7组～12组的改进马氏距离值呈上升趋势(改进马氏距离的大值的频次贡献率越来越大)，而第1组～6组的改进马氏距离的频次贡献率越来越小，采样点117组之后健康指数呈上升趋势，说明在采样点108组设备出现了劣化故障，并最终导致采样点137组退化指数超过了阈值，可以认为是设备逐渐退化的过程。采样点158组以后，即使改进马氏距离值低于阈值，但是相应的退化指数依然在阈值附近上下波动，可见设备已经发生了退化，处于非健康状态。

4 结束语

首先利用改进马氏距离，将多维变量问题降维。为了更好地判定设备健康状态，结合构建的退化指数这一新的度量指标，客观的把变动的改进马氏距离分组成直方图，再通过滑动窗口，将领近时间点的历史信息纳入到健康指标体系中，退化指数超过了阈值表征系统发生退化。实验表明，该方法有效地减少了空压机设备假报警的次数。配合分析故障时刻的电压电流波形，验证了该结论的正确性。即使后期改进马氏距离已经低于阈值，利用退化指数仍然可以持续检测出设备的退化状态。可见，退化指数这一度量指标相对于直接利用马氏距离可以可靠地诊断故障和退化状态，在评估设备健康状态上更具备鲁棒性。该方法不局限于空压机设备，对设备或系统的状态量和阈值进行修改，即适用于任何一个不同生命周期下性能参数可测的设备或系统。