基于多分类概率输出模型的变压器故障诊断*

王鹤，姜鸿儒，王振丁

(1. 东北电力大学，吉林 吉林 132012； 2. 国网山东省电力公司黄岛供电公司，山东 青岛 266000)

0 引 言

电力变压器作为电力系统中能量转换、传输的核心，能否快速、准确地诊断出变压器故障，直接影响系统的安全、稳定运行[1-2]。我国目前已有较多变压器在长期运行过程中出现绝缘老化、材质劣化等故障隐患，这将导致发生事故的概率不断增加[3]。由此有必要采取合理的方法来及时的发现变压器潜伏性故障，进而预防和降低事故发生的概率[4]。

目前，变压器油中溶解气体分析法(Dissolved Gas Analysis，DGA)已成为诊断和检测变压器内部故障性质的重要方法[5]。基于DGA已形成了IEC推荐的三比值法、Rogers法等传统诊断方法[6-7]。随着人工智能技术的发展，国内外学者将人工神经网络 (ANN)[6]、贝叶斯分类器[8]、极限学习机(ELM)[9]和支持向量机(SVM)[10]等人工智能算法引入到变压器故障诊断领域，为电力变压器故障诊断技术的发展提供了新思路。其中，支持向量机因所需训练样本数据少、泛化能力强等优点广泛应用于变压器故障诊断中[11-12]。文献[12]利用布谷鸟算法对SVM的参数进行寻优，利用优化后的SVM模型进行变压器故障判断。文献[13]利用建立的快速相关向量机多层次分类模型减少了模型的训练时间，并利用量子粒子群算法优化了模型参数，提高了诊断的精度。文献[14]利用多核学习向量机将模型分解为2个凸优问题进行求解，降低了计算复杂度。以上基于SVM的智能算法最终均是以故障类型作为诊断的结果，但是考虑到变压器结构复杂，故障现象与故障特征间存在着模糊性，其仍存在误诊断问题。

提出一种基于MCPO模型的变压器故障诊断方法，其在继承了SVM优点的基础上，通过利用Sigmoid函数实现SVM的概率输出，进而综合多个二分类输出结果，将模型的求解转化为一个凸二次规划求解问题实现多分类概率输出。该方法能够判别故障特征是否明确，减少了对变压器故障的误判，仿真结果验证了基于MCPO模型的变压器故障诊断方法的有效性。

1 基于SVM的MCPO模型

所建立的基于SVM的MCPO模型是在传统SVM方法的基础上，通过引入Sigmoid函数将SVM的决策函数输出映射为二分类概率输出，进而综合多个二分类输出结果，将模型的求解转化为一个凸二次规划求解问题实现多分类概率输出。

1.1 SVM

支持向量机的本质是在训练样本数据中找出用于构造最优分类超平面的支持向量，在数学上可归结为求解一个二次优化问题[12]。

对于线性可分的样本，其可被最优分类超平面区分开，超平面方程为：

ex+f=0,e∈Rn,f∈R

(1)

式中e为超平面法线；f为分类阈值；n为样本空间维数。

设一组样本(xi，yi)，xi为样本数据，yi为样本类别标志。最优分类超平面问题的求解可转化为求解带约束条件的优化问题：

(2)

式中l为训练样本总数。

对于线性不可分的样本，在约束条件中引入松弛变量βi来解决分类误差问题，则约束条件可表示为：

yie·xi+f≥1-βii=1,2,…,l

(3)

由此可得到线性不可分时的最优分类面，其可表示为如式(4)所示的优化问题:

(4)

式中C(C>0)为惩罚参数，其作用是控制对错分样本的惩罚程度。

利用拉格朗日函数求解上述优化问题：

(5)

式中ai为拉格朗日乘子。

对于非线性问题，SVM通过引入核函数实现某一非线性变换后的线性分类。文中采用RBF作为模型的核函数：

(6)

式中σ为RBF函数宽度参数。

则SVM的分类决策函数为：

(7)

1.2 MCPO模型

采用文献[15]的方法利用Sigmoid函数将g(x)映射在区间[0,1]，则概率输出表达式：

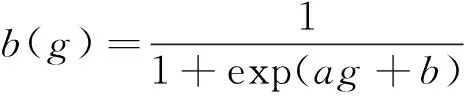
(8)

式中a，b为Sigmoid函数的待定参数。

Sigmoid函数的参数a，b可通过最小化交叉熵误差函数获得，其求解模型可表示为：

(9)

其中：

(10)

式中M是样本类型为yi=1的样本个数；M′是样本类型为yi=-1的样本个数。

式(10)可利用牛顿法获得最优解，即令G(a，b)的梯度矩阵等于0时的解为最优解。G(a，b)的梯度矩阵如式(11)所示。

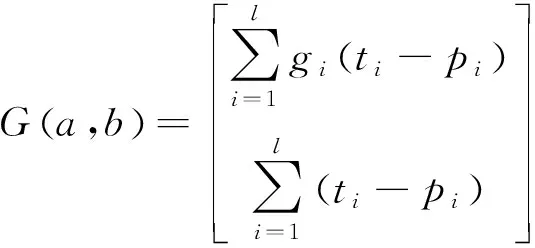
(11)

获得参数a，b后，则可利用Sigmoid函数将g(x)映射成概率输出形式。对于一个二分类问题，利用式(8)可获得x属于某一类(w或v类)的概率估计swv：

(12)

电力变压器的故障类型众多，其诊断的过程应属于多分类问题。一个m分类的问题应该综合考虑1/2m(m-1)个二分类SVM的结果，进而将其swv综合为多分类的概率输出，则x为每一类的概率pw可表示为：

(13)

利用文献[16]给出的从二分类概率得到多分类概率的方法实现多分类的概率输出。考虑有：

(14)

即：

swv/svw≈pw/pv

(15)

对上式进行变换并求和：

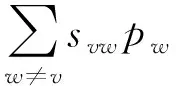
(16)

利用式(16)求解以下模型进而获得pw：

(17)

上述模型的求解可转化为求解一个凸二次规划问题：

(18)

当满足式(19)时，其获得最优解。

(19)

式中e=[1,1, …,1]T，pT=[p1,p2, …,pm]。基于SVM的MCPO模型构建流程见图1。

2 基于MCPO模型的变压器故障诊断

2.1 选取输入、输出向量

MCPO模型的输入为(x，y)，其中x是DGA数据中H2、CH4、C2H6、C2H4、C2H2这五种气体含量，分别记作x1、x2、x3、x4、x5，则特征向量x=(x1、x2、x3、x4、x5)；特征向量y为故障类型，所考虑的故障类型如表1所示。

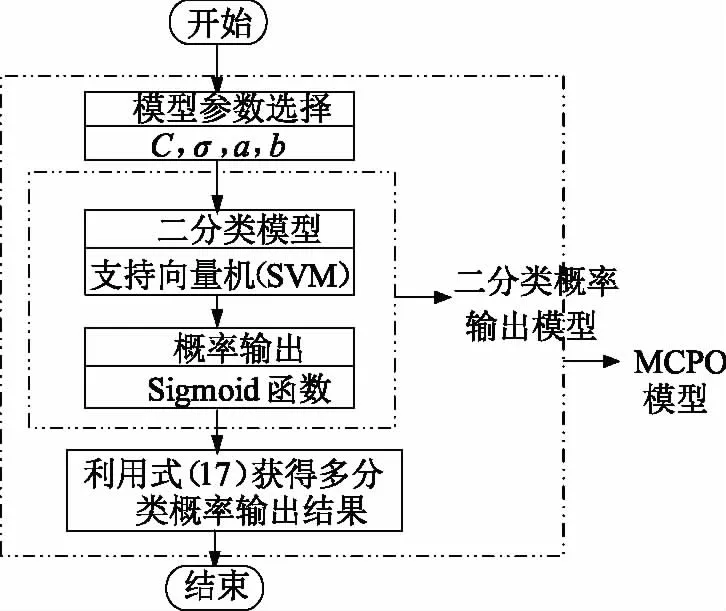
图1 MCPO模型构建流程

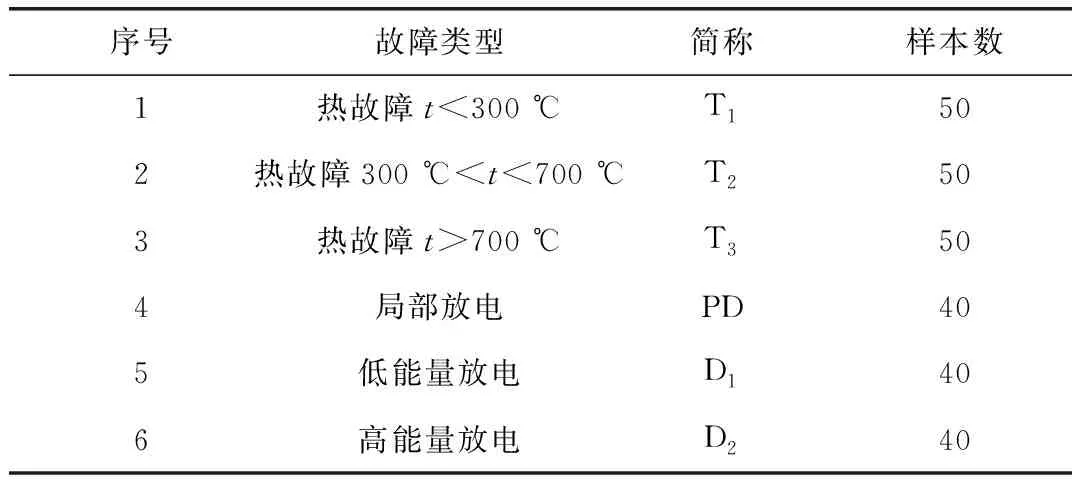
序号故障类型简称样本数1热故障t<300 ℃T1502热故障300 ℃700 ℃T3504局部放电PD405低能量放电D1406高能量放电D240

MCPO模型的输出为(pT1，pT2，pT3，pPD，pD1，pD2)，pT1，pT2，pT3，pPD，pD1，pD2分别代表变压器的状态为T1，T2，T3，PD，D1，D2的概率。考虑到DGA数据中各气体含量存在较大差异，将各种溶解气体含量换算为[0,1]范围内的相对含量，按照式(20)对DGA数据进行归一化处理。

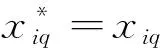
(20)

式中xiq为第i个样本第q类故障气体的含量。

2.2 模型参数的选择

所提出的MCPO模型，其参数(C，σ)的选择对提高故障诊断的准确率至关重要。因此，采用网格搜索的方法，对训练样本集进行交叉验证，并选择其中准确率最高的一组(C，σ)作为模型的参数。同时，实现概率输出还要形成Sigmoid函数的参数训练集，同样利用交叉验证的方法形成Sigmoid函数的参数训练集(gi，yi)。获得最优参数的流程如下:

(1)给定参数(C，σ)；

(2)将样本随机分成k个互不相交的子集，每次选择一个子集作为测试集，其他作为训练集；

(3)训练SVM，计算验证集gi；

(4)k个子集交叉验证形成Sigmoid函数的训练集(gi，yi)，训练Sigmoid函数的参数a，b；

(5)计算全部swv，得到多分类概率估计pw，若完成对所有子集的计算，则计算交叉验证的准确率。否则，返回到第二步。

2.3 诊断流程

(1)数据处理，归一化输入特征向量，形成训练、测试集样本；

(2)确定最优参数(C，σ)；

(3)利用最优参数训练SVM及Sigmoid函数的参数a、b，进而获得诊断模型；

(4)应用诊断模型对测试样本进行故障诊断。

3 算例分析

选择了270组已确定故障类型的DGA数据进行研究，并将样本数据按2∶1比例分为训练集和测试集。模型参数(C，σ)分别在取值范围[2-15，2-14，…，214，215]，[2-7，2-6，…，26，27]内以指数增长方式获取。将训练样本分为5组进行交叉验证，得到的最优参数为(2-1，23)。表2列举了10组测试样本的DGA数据。表3给出了MCPO模型的诊断结果。

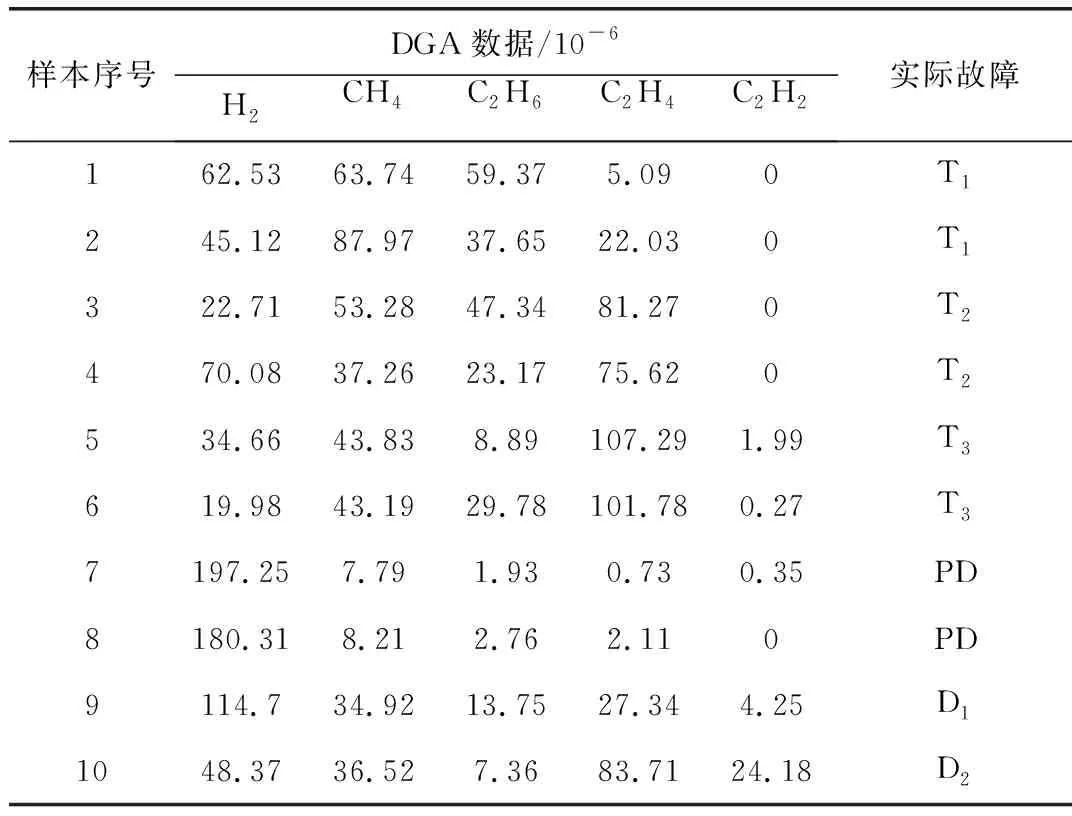
表2 测试样本DGA数据

由表2可知，MCPO模型的诊断结果是变压器的状态为每类故障的概率。如果将概率最大作为判断故障类型的依据，基于MCPO模型的故障诊断正确率为90%。考虑到上述方法在故障特征不明显(样本故障分类概率相差较小)的情况时存在一定的误判，因此本文进一步对诊断判据进行研究。

利用MCPO模型的故障诊断数据，提出基于最大概率Pm和标准差ε的两种故障诊断判据。其中，Pm=max{p1、p2、p3、p4、p5、p6}，ε为{p1、p2、p3、p4、p5、p6}的标准差。为了能够方便的说明Pm和ε的意义，对测试样本进行分类。分类原则如下：如果MCPO模型的诊断结果中概率最大的故障为实际故障，则样本标记为Rh，若不是样本标记为Rl。

由表2、表3可知，依据上述分类原则样本3属于Rh，此时Pm=83.79%，ε=0.301。样本4属于Rl，此时Pm=43.17%，ε=0.15。结果表明，故障特征显著的样本，Pm和ε的取值较大；故障特征不显著的样本，Pm和ε的取值较小。

表4给出了基于上述分类原则，所有测试样本的分类结果。

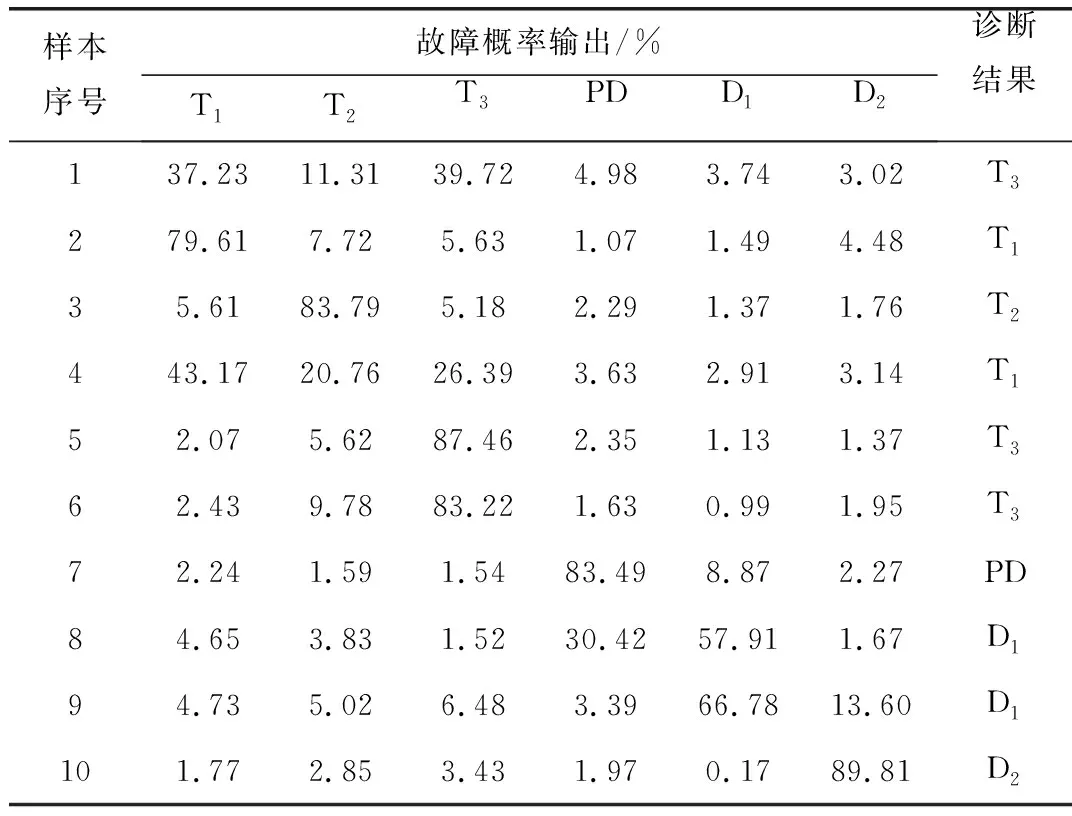
表3 模型诊断结果

表4 测试样本分类结果

表4中，Pmax-z和εz为Pm和ε的平均值。由表4可知，样本集Rh中Pmax-z和εz的值均大于样本集Rl中的值。以上分析结果表明，故障特征明显的样本，样本故障分类概率相差较大，Pm、ε取值较大；故障特征不明显的样本，样本故障分类概率较为接近，Pm、ε取值较小。因此，可以利用Pm和ε表征样本的故障特征是否显著。计算了所有测试集的Pm和ε，计算结果见图2。

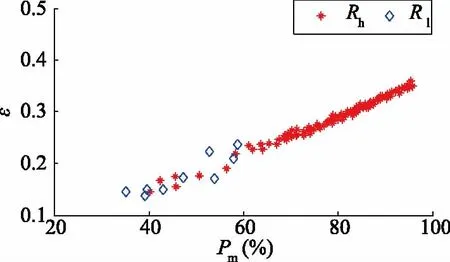
图2 Pm、ε计算结果

由图2可知，对于故障特征不明确的样本主要分布在Pm<0.6和ε<0.25的区域中。因此，本文给出判断标准为Pm=0.6和ε=0.25，即认为Pm<0.6且ε<0.25的样本为故障特征不明确的样本，对于这类样本需要利用MCPO模型的诊断结果针对可能存在的故障做出相应的校正措施。

表5列举了采用SVM方法和MCPO方法对同样的样本进行故障诊断得到的结果。

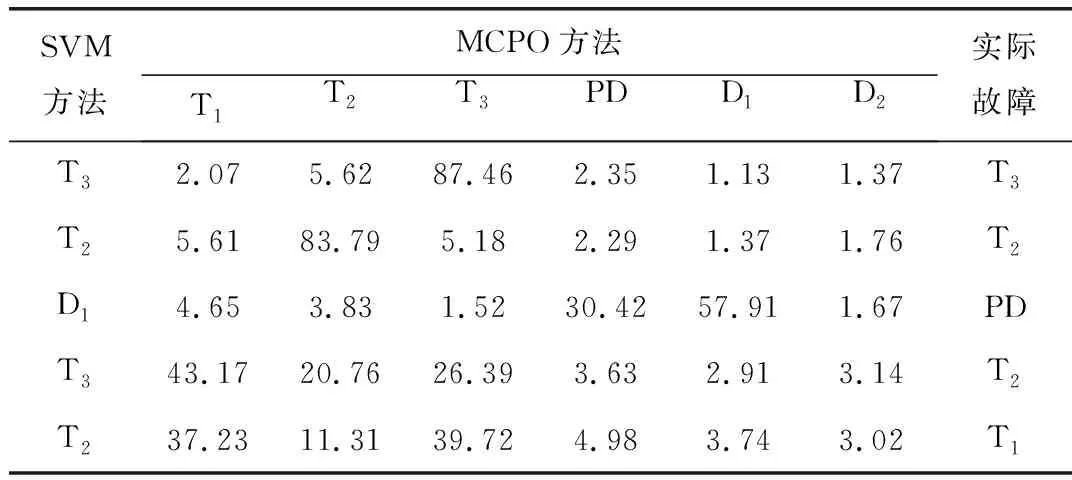
表5 不同诊断方法的比较

由表5可知，故障特征显著的样本利用SVM方法和MCPO方法都能有效的辨别故障类型；故障特征不显著的样本，利用SVM方法会导致误诊断，而MCPO方法可利用基于最大概率Pm和标准差ε的两种故障诊断判据有效的辨识故障特征不显著的样本，对于这类样本，可参考概率较大的两三个故障类型进行相应的校正措施，弥补了传统SVM方法在辨别故障特征不明确的样本时会导致误诊断的问题。

4 结束语

提出的基于多分类概率输出模型的变压器故障诊断方法分类效果较好，并能够提供概率信息。针对故障特征不明确的样本，可参考概率较大的两三个故障类型进行相应的校正措施，进而降低了对变压器故障的误判。通过仿真分析验证了基于最大概率Pm和标准差ε的两种故障诊断判据的有效性，为进一步开展合理的校正措施提供了一定的依据。