电力线信道系统噪声的建模方法研究*
胡苏阳,王莉,杨善水
(南京航空航天大学 自动化学院, 南京 211106)
0 引 言
复杂大系统(飞机、航空航天系统、核及可再生能源系统)的飞速发展促使电力线的使用日益增多,结构交错密布,实际电力线信道具有衰减大、噪声严重的问题[1-3],对信息传输和故障诊断有较大干扰。因此对电力线信道传输特性建模研究引起国内外学者的广泛关注[4-6],在现有电力线系统噪声建模研究中[7-10],信道噪声普遍采用传统分类,主要包括有色噪声、窄带噪声、脉冲噪声[4]。然而实际航空电缆中电弧故障已成为普遍现象,给电网带来高度非线性、时变性以及不可预测性的电弧噪声,导致飞机配电网电压畸变等问题,这给航空航天系统的可靠工作以及电力线故障的准确检测定位带来极大挑战;且电气系统中的电弧故障可能会中断电源供电、损坏电力设备、引起火灾甚至威胁人类生命安全。因此亟需建立适应多条件的、更加全面、准确的电弧噪声模型,将电弧噪声与典型电力线噪声相结合,进一步完善电力线信道噪声特征,建立更加全面的电力线系统信道模型。
1994年,意大利博洛尼亚大学的Montanari G C等学者将电弧电压定义为电弧长度的函数,弧长的时变性通过叠加带通白噪声得到[11]; 1996年,美国克莱姆森大学的Srinivas Varadan等学者通过简化电弧炉负载u-i特性曲线得到电弧电压表达式[12],将带通白噪声叠加于电弧电阻上模拟负载电阻的时变性; 2008年,上海交大的王育飞,潘艳霞[13]等通过直接叠加带通白噪声于确定性电弧电压上,得到用于电压波动与闪变研究的电弧炉随机模型。但以上模型建模较复杂,只能适用于特定的环境。当外界环境改变时,需要专业人员重新考虑方程的合理性,其通用性有待提高。
文中主要研究内容如下:首先对典型电力线噪声进行分类并分析其不同特性,建立典型电力线噪声模型;然后结合实验平台中采集得到的电弧数据,提出基于分数阶滤波器的电弧噪声建模方法以及基于数据驱动的电弧噪声模型参数确定方法;最后通过仿真和实验结果验证模型的准确性。
1 电缆信道噪声特性仿真与分析
电缆信道环境中的噪声按大类可分为有色背景噪声、窄带噪声、脉冲噪声[14](包括工频异步周期脉冲噪声、工频同步周期脉冲噪声等),其中还包括一些复杂电气现象带来的复合噪声,如电弧噪声,呈现高度不确定性与随机性,文中基于Matlab对这些噪声特性进行分析并建模。
1.1 典型电缆信道噪声
1.1.1 有色噪声
有色背景噪声来自各种低功率噪声源,如电脑,调光器等,其频谱较宽且持续存在。从时域角度来看,有色背景噪声的产生过程,即白噪声信号w(n)通过一个特定的滤波器H(z)得到输出的有色背景噪声x(n)。
噪声整形滤波器模型的传递函数如下所示:
(1)
式中函数的分母A(z)表示的是自回归AR部分;ai和p是滤波器的系数和阶数,将典型白噪声序列通过线性稳定滤波系统H(z),即能表示出噪声的产生过程。
1.1.2 窄带噪声
窄带噪声通常由调制的正弦波叠加而成,主要由中短波广播等无线信号在电力线信道中引起的串扰而产生,其频带较窄,可通过式(2)所示的N个独立的正弦函数叠加生成。
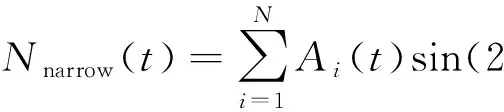
(2)
式中Ai(t)是对信号近似的调制幅值;φi表示相位,在0~2π之间随机产生;fi为各正弦信号频率。
1.1.3 工频同步的周期脉冲噪声
工频同步的周期脉冲噪声主要由整流器件产生,伴随高能量高次谐波,整流器件在每个工频周期内产生两次冲击电压,导通一次,截止一次,重复频率为50 Hz或100 Hz。其特点是持续时间短,脉冲强度高于背景噪声。电缆上的脉冲噪声可以由衰减的正弦波叠加而成,文中采用指数规律衰减的正弦信号来表示,考虑到整个时间轴上脉冲出现的时间,时间轴上所有工频同步周期脉冲噪声可表示为:

(3)
式中A为脉冲幅度0~45 dB;l为整流器件冲击电压的个数;tarr为单个脉冲出现时间;f为衰减正弦波频率,脉冲周期为0.02 s,脉冲宽度τ由整流器件导通或截止时间决定。
1.1.4 工频异步的周期脉冲噪声
工频异步的周期脉冲噪声主要来源于计算机显示器的扫描谐波等,与工频同步周期脉冲噪声不同的是,其出现频率由显示器的扫描频率决定。文中工频异步脉冲噪声采用指数规律衰减的正弦信号叠加产生,可表示为:
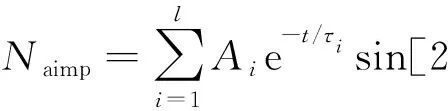
(4)
1.2 电缆信道电弧噪声
电弧是指由于电场过强,气体发生电崩溃而持续形成等离子体,使得电流通过通常状态下的绝缘介质(例如空气)的现象。当电弧产生并稳定燃烧后,电弧电流中还存在着电弧电流交流分量,该交流分量分布不具有周期性,呈现为一种噪声的特性,该噪声主要来源于电弧阴极鞘层区的射频信号[15]。
对电弧噪声特征的建模首先需要利用电弧模拟发生装置对故障进行模拟,并准确采集电弧电流、电弧电压、电弧电流交流分量等电气特征量,分析其时域及频域特征。图1所示为电弧故障模拟、测试自动化研究平台。

图1 电弧故障模拟、测试自动化研究平台实物图
使用铜作为阴极、碳作为阳极,输入电压恒定为270 V,27 Ω电阻作为负载,利用电动电弧发生器产生不同弧长的电弧。采集电弧电流交流分量进行FFT分析,频谱图如图2所示,从图中可以看出随着弧长的增大,在低频段电弧电流频谱幅值不断的增加,呈现为不同衰减速率的有色噪声。
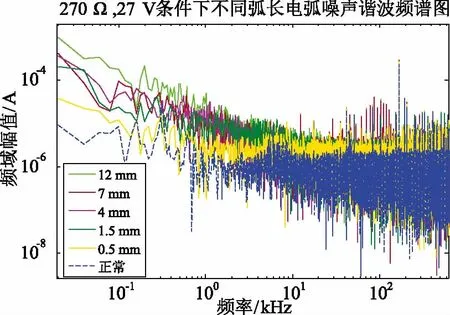
图2 电弧噪声谐波频谱随弧长变化对比图
根据图2中分析的特性,电弧噪声分为两个频带,分别为幅值随频率增加而衰减的低频带,近似于有色噪声;幅值基本保持不变的高频带,近似白噪声。文中基于Matlab,利用白噪声模块产生随机噪声,并设计滤波器,基于建立实际情况相符的电弧噪声模型。
1.2.1 基于分数阶滤波器的电弧噪声建模方法
采用单极点单零点的PI补偿网络设计滤波器,滤波器的传递函数为:
(5)
需要利用分数阶微积分的思想,构造满足指定传递函数的滤波器,以调整幅值衰减的速率,用一个有限的整数阶微分方程来近似描述分数阶系统。对于形如G(s)=su,α∈(0,1)的传递函数,使用分数阶的方法步骤如下:
(1)给定需要等效的近似频段的范围[1/v,v],及近似的阶次M。近似阶次M越大,拟合效果越好,但计算量会大大增加。实验表明,阶次M通常取4时,得出的结果以及各方面因素是令人满意的,因此,文中采用近似阶次M=4;
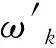
(6)
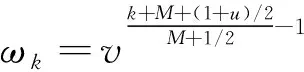
(7)
K=v-u
(8)
(3)由式(9)计算出分数阶传递函数G(s)=su的等效整数阶有理传递函数形式:
(9)
在得到分数阶传递函数后,还需要对白噪声进行放大或缩小一定的倍数w,所以最终的传递函数表达式为:
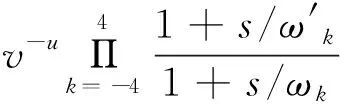
(10)
该方法中的分数阶滤波器的参数需要确定,包括滤波器的阶次u、滤波器截止角频率v,放大倍数w。这三个参数是为了拟合电弧噪声特性而提出的,并无实际的物理意义,只能通过人工反复调整参数实现仿真与试验波形的吻合。而这种方式只能反映单次试验时的电弧噪声随机性特征,当电弧发生条件改变时,需要重新确定参数,不具有通用性。
1.2.2 基于数据驱动的电弧噪声模型参数确定方法
数据驱动方法能够通过分析研究对象的数据,分析系统变量的内部逻辑关系,离线或在线学习计算与当前状态下匹配的模型数据。提出使用数据驱动的方法确定故障电弧随机性噪声模型中的参数,采用离线数据计算不同工作条件下参数的变化。
对于每一次试验采得的数据,均需要待定电弧随机性模型的参数:滤波器的阶次u、滤波器截止角频率v,放大倍数w。因此,采用遍历法对每一个参量进行遴选,以使得拟合得到的频谱结果与实验结果最接近。为了能够定量评定拟合的效果,采用电流在低频段(0~50 kHz)的谐波幅值和判断滤波器的阶次u、滤波器截止角频率v拟合效果,采用电流在高频段(200 kHz ~500 kHz)的谐波幅值和判断放大倍数w。
具体的步骤如下:
(1)读入实验数据,对其进行FFT分析,计算得到试验数据的低频段和高频段谐波幅值和;
(2)设定滤波器的阶次u、滤波器截止角频率v,放大倍数w的初值;
(3)利用上文中的方法,计算得到分数阶滤波器的表达式;
(4)使用分数阶滤波器对N(0,1)的白噪声进行滤波,并对滤波后的波形进行FFT分析,计算得到仿真数据的谐波幅值和;
(5)计算试验数据与仿真数据的谐波幅值和之间的误差;
(6)将误差与误差最小值相比,当误差大于最小误差时,更新最小误差,并记录下此时的u,v,w;
(7)重复步骤(2)~步骤(6)直至遍历所有的u,v,w值后结束循环,输出此次试验下,误差最小时的u,v,w。
对电弧电流交流分量离线数据进行拟合,获得的电弧噪声模型拟合频谱结果如图3所示。
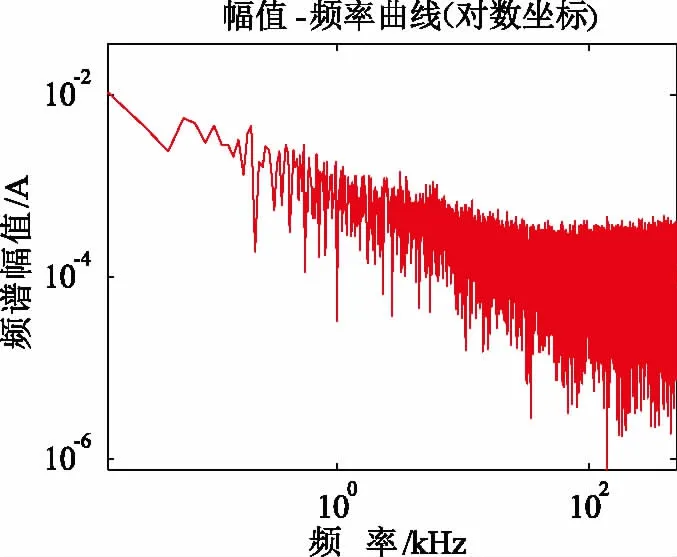
图3 电流6 A弧长11 mm的电弧噪声模型拟合频谱
2 电缆信道系统噪声模型实验验证
利用图1所示电弧故障模拟、测试自动化研究平台对电力线信道噪声模型进行实验验证。拟合电弧噪声与实测数据的频谱对比图如图4所示,电弧噪声谐波的仿真波形与实验波形基本契合,在4 Hz~2 kHz频段内呈现有色噪声的特性,在2 kHz~500 kHz频段内呈现出白噪声的特性,能够较好的还原电弧噪声谐波分量的频域信息。
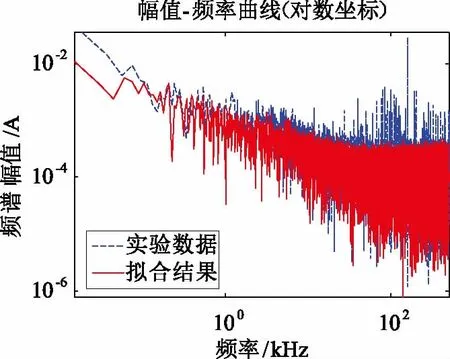
图4 电流6 A、弧长11 mm的电弧噪声模型与实测数据频谱图对比
求取相同弧长、不同电流时的谐波幅值和如图5所示,□和○分别表示实验和仿真获得的频域特征平均值结果。从图中可以看出,实验结果与仿真结果的频域特征量统计区域较为吻合,计算得统计平均误差为15.3%。
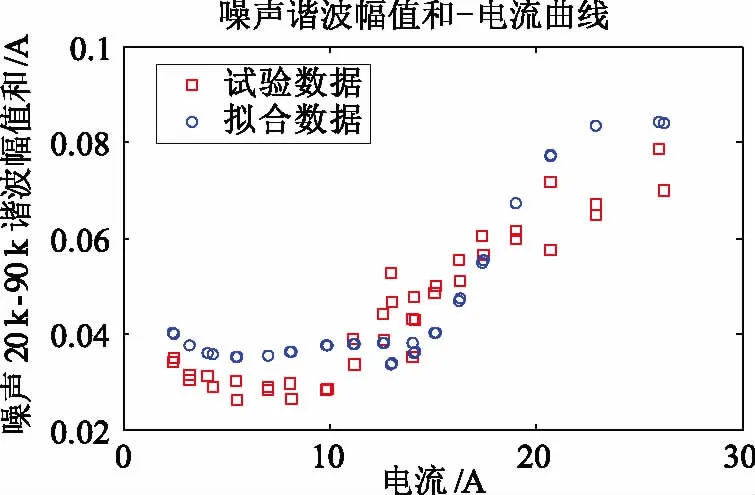
图5 不同电流下1mm弧长电弧噪声频域特征
为了验证模型对外界条件变化的适应程度,比较电极改变时电弧电流的时域特征,采用碳为阴极,铜为阳极,同样比较相同电流(20 A)不同弧长的频域特征量,如图6所示,□和○分别表示实验和仿真获得的频域特征平均值。在电弧弧长小于15 mm时,此时实验结果与仿真结果的频域特征量误差较小,统计平均误差为5.7%。而当电弧弧长大于15 mm时,实验结果频域特征量随弧长增大而减小,仿真结果则基本维持不变,此时拟合误差稍大,统计平均误差为25.8%。
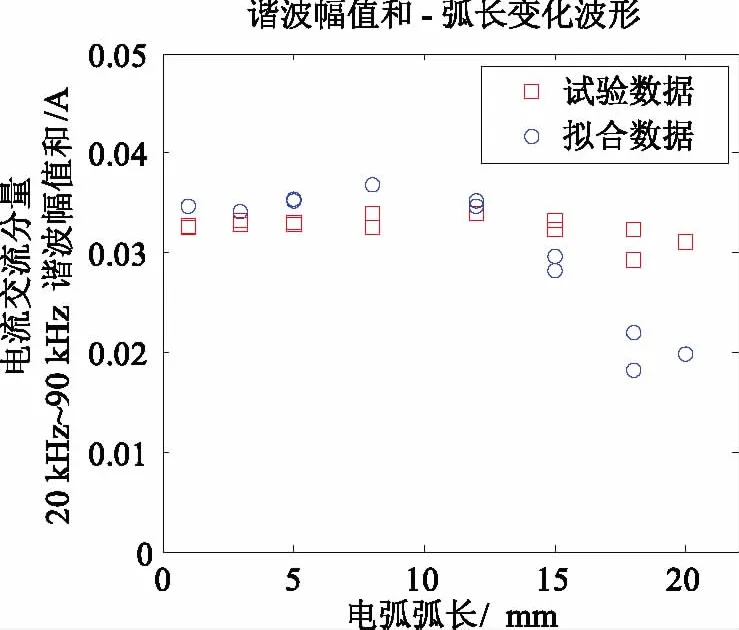
图6 不同弧长下20 A电弧电流频域特征
对电力线中的窄带噪声模型与实验数据的时频域对比如图7所示。
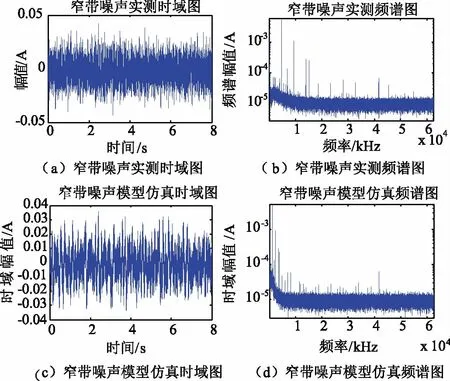
图7 窄带噪声模型与实测对比图
对电力线中工频同步脉冲噪声模型与实验数据的时域对比如图8所示。
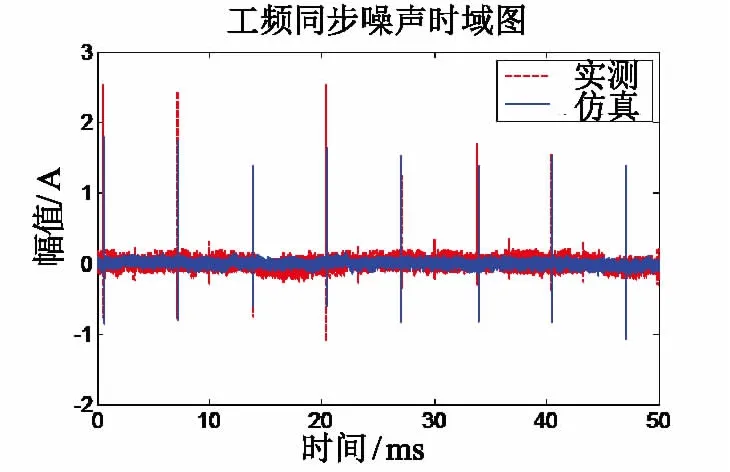
图8 工频同步脉冲噪声模型与实测对比图
对电力线中工频异步脉冲噪声模型与实验数据的对比如图9所示。
考虑到时域波形受电网环境随机性的干扰误差,噪声模型对噪声的时域、频域特性的分布拟合较为准确,验证了模型对典型电力线噪声拟合的准确性。
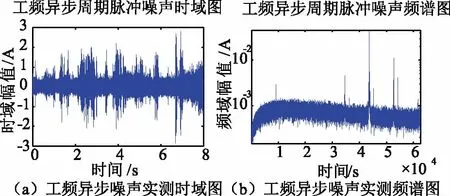
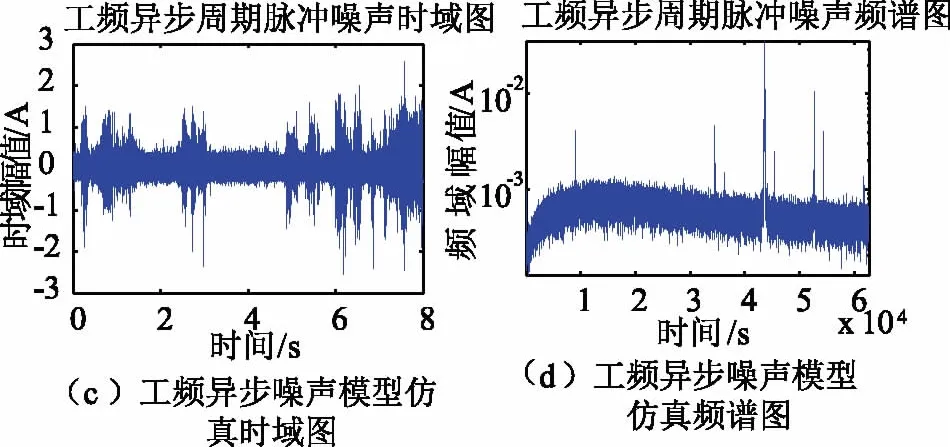
图9 工频异步脉冲噪声模型与实测对比图
3 结束语
对电力线信道典型噪声的不同特性进行分析,并提出基于分数阶滤波器的电弧噪声建模方法以及基于数据驱动的电弧噪声模型参数确定方法,完善了电力线信道噪声模型,通过理论分析、仿真和实验验证得到以下结论:
(1)电弧噪声在4 Hz~2 kHz频段内呈现有色噪声的特性,在2 kHz~500 kHz频段内呈现出白噪声的特性;
(2)提出的电弧噪声模型可以模拟不同电流、弧长条件下的电弧高频噪声特性。随着电弧电流的增大,其高频噪声谐波幅值和具有先减小后增大的趋势;
(3)在碳为阴极、铜为阳极时,在0~30 A状态下对0~15 mm弧长电弧实验结果拟合效果较好,在15 mm以上弧长状态下,实验结果频域特征量随弧长增大而减小;
(4)将典型电力线噪声模型和所提出的电弧噪声模型相结合,进一步建立了更加完善、准确的电力线信道系统噪声模型,为后续开展电力线故障诊断技术的深入研究奠定了基础。

