基于人工鱼群算法的波浪发电系统最优负载*

邹子君，杨俊华，杨金明，王子为

(1.广东工业大学 自动化学院，广州 510006； 2.华南理工大学 电力学院，广州 510641)

0 引 言

最大波浪能捕获是波浪发电研究的关键技术，为提升波浪发电系统的平均输出功率，已涌现各种控制方案。文献[1]提出了一种变步长扰动观察法，用于实现浮标式波能转换装置的最大功率点跟踪。算法根据输入功率的数值范围，决定相应的变步长规则，缓解了算法跟踪速度与精度的矛盾。仿真表明，该算法减少了装置的输出功率值与理论最大值间的稳态误差，提高了装置对不同波浪环境的适应性。但扰动观察法的固有缺陷—最大功率点附近的功率振荡会影响装置的稳定性。针对振荡水柱式波能转换装置，文献[2]提出一种最大捕获宽度跟踪控制器(MCWT)，与传统锁存时间固定的控制器不同，该控制器可根据实际海浪条件自适应调节锁存时间长度。同时，MCWT控制器的设计过程不需要系统的数学模型，假设条件与海浪条件差异不会影响实际控制效果。仿真表明，MCWT控制器可提高随机波浪条件下装置的鲁棒性，增加波浪能捕获功率值。但MCWT控制器需要传感器测量波幅和波能转换装置的功率，实现成本较高。

为实现液压动力输出波能转换装置的最大波浪能捕获，文献[3]提出分离控制方案，基于庞特里亚金最大值原理设计控制率。仿真表明，与伪连续控制相比，分离控制能够增加规则波下转换装置的波浪能捕获宽度，不规则波浪条件下的输出功率平均值也提高了47%。但该方法需提供波浪激励力的预测值，在实际中不易实现。与典型的浮标式波能转换装置不同，可调倾角油压动力输出波能转换装置(ASAWEC)能够从波浪的起伏运动和浪涌中捕获波浪能量，为实现该装置的输出功率最大化，文献[4]提出了学习向量定量神经网络控制算法。通过数据集训练神经网络控制器，分类不同波形条件所对应的最佳倾斜角度，采用PI控制器，可在2 s内将装置倾斜角调节至最佳值，实现输出能量最大化。该算法有效性已得到规则波和不规则波条件下的仿真验证，实际海浪条件的适用性有待进一步研究。

模型自由控制策略(MFC)，不依赖于控制对象的数学模型，特别适于波浪发电类难以建立精确数学模型且实际动态性能复杂未知的系统。为优化单体波浪能转换装置振荡控制，文献[5]采用MFC策略，能够实现浮子速度与最佳速度跟踪误差的最小化，将输出功率的峰均比从11.7大幅降至6.8，增加输出功率平均值。并对参数不确定性、外部干扰等具有鲁棒性，可将这些不确定因素造成的功率降幅减少一半。实际控制效果有待实际实验验证。

针对阿基米德摆式永磁同步直线波浪发电系统，文献[6]提出了无速度传感器控制，通过无迹卡尔曼滤波器估计直线发电机动子速度，从电机瞬时输出有功功率获得与波浪频率匹配的最佳速度值，采用PI控制器跟踪该最佳值，从而满足Falnes提出的相位条件[7]，最大限度捕获波浪能。

为优化波能转换装置的功率控制，文献[8]提出了分层控制方案，通过求解浮子振荡幅度约束条件下的最大吸收功率，产生参考速度。采用滑模变控制方法，调节浮子实际振荡速度跟踪最佳速度。仿真结果表明，与模糊控制、反应式控制相比，分层控制可提高装置对非线性因素、扰动的鲁棒性。但由于不规则波浪条件下产生的参考速度是对应波峰频率的，分层控制只能是一种次优控制。

通过优化算法求解波浪发电系统的最优负载，是一种实现最大波浪能捕获的有效途径。传统粒子群算法易使波浪发电系统负载值陷入局部最优，文中提出一种基于动物行为的人工鱼群智能优化新算法，该算法已应用到微网可再生能源调度优化[9]、不均匀光照下光伏发电系统的MPPT控制[10]等问题中。通过比较“追尾或觅食或随机”和“聚群或觅食或随机”两种组合行为得到的下一位置目标函数值大小，确定搜索方向，可增加搜索过程的灵活性。仿真结果表明，该算法可大幅增加波浪发电系统的平均输出功率。

1 浮子的运动方程

图1给出了振荡浮子式波浪发电系统结构图。

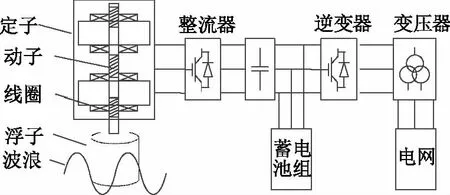
图1 振荡浮子式波浪发电系统结构图

结构由浮子、直线发电机、电力电子变换器、储能单元等模块组成。浮子在波浪中运动时，不仅会引起阻尼力，还会受到重力和静水压力联合作用引起的静水恢复力的作用。根据波浪理论[11]，静水恢复力及阻尼力的表达式为：

(1)

式中Fs(t)是静水恢复力；Fr(t)为阻尼力；Ks是恢复力刚性系数；Rr是阻尼力阻尼系数；x为垂直方向上浮子偏离平衡位置的位移；t为时间。

浮子随波浪振荡时会产生辐射波，辐射波与海水相互作用会产生辐射力，可将辐射力表示为辐射阻抗与速度的乘积[11]：

(2)

式中FR(t)是辐射力；RR是因辐射力产生的附加阻尼；XR是因辐射力产生的附加电抗。

由牛顿力学，可得浮子的运动方程[11]：

(3)

式中m为浮子质量；Fex(t)为海浪激励力，表示入射波作用于浮子上的力。

将上述Fs(t)、FR(t)、Fr(t)的表达式代入式(3)，可得：

(4)

整理后得：

(5)

对式(5)进行傅里叶变换，可得：

(6)

将s=jω代入式(6)，可得：

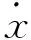
(7)

通常将附加电抗表示为[11]：

(8)

式中mR是因辐射力产生的附加质量。

将式(8)代入式(7)，可得：

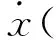
(9)

变换式(9)，得到：

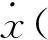
(10)

2 系统平均输出功率的分析

系统输出的平均功率为[11]：

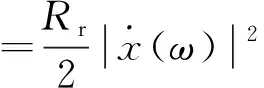
(11)

从式(10)可得：

4）加强田间管理。重视提高麦田沟厢质量，降低田间含水量，为小麦根系发育创造良好的土壤环境，增强小麦自身的抗倒伏能力。根据植保情报，做好小麦病害综合防治工作。

(12)

将式(12)平方后，代入式(11)：

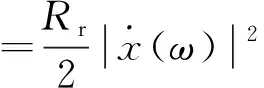
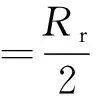
(13)

式中在一定频率下，参数Fex(ω)、ω、RR、Ks、mR、m均为常数，因此可对式(13)进行标么化处理，得：

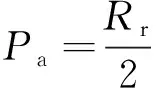
(14)

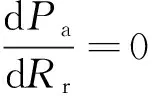
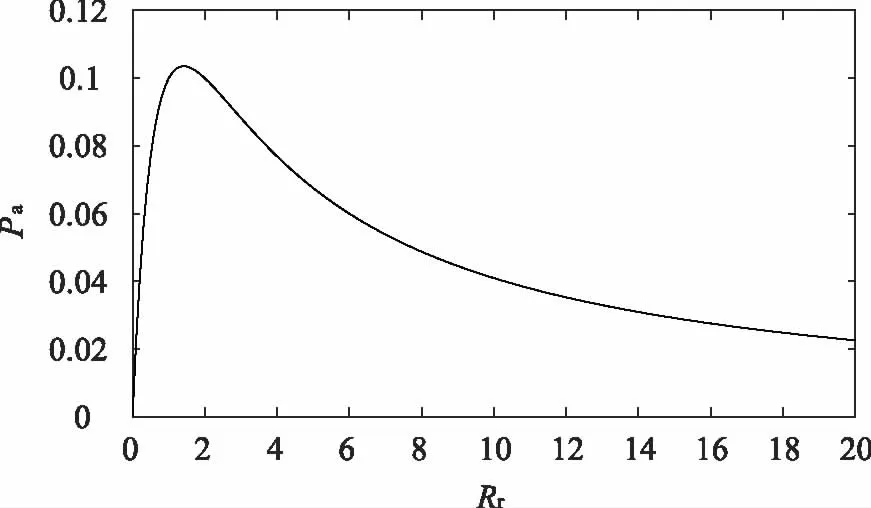
图2 波浪发电系统输出平均功率的曲线图

对Pa的表达式，即式(13)求导可得：

(ωm+ωmR-Ks/ω)2]-2Rr(Rr+RR)=0

(15)

求解后可知Rropt的表达式为：

(16)

将式(16)代入式(13)，可得Pa的理论最大值:

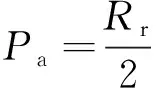
(17)

式中的海浪激励力Fex频率与波浪运动频率保持一致[12]，因此一定频率下Fex的数值是固定的。从图2可知，不同频率下的最大功率点对应着唯一的一个Rr。于是，为寻求波浪发电系统的最优负载，增加输出功率平均值，可利用人工鱼群算法的寻优能力，通过迭代计算，迅速找到不同频率下的Rropt，使Pa与Fex的比值满足：

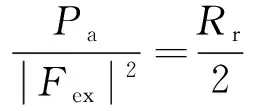
(18)

即可实现不同频率下系统输出功率最大化。

3 人工鱼群算法

人工鱼群算法是一种基于动物行为的群体智能优化算法，通过模拟鱼群的觅食、追尾、随机、聚群等行为在搜索域中进行寻优，求解优化问题。应用于波浪发电系统的最优负载求解问题，收敛速度快并具有取得全局极值能力。

首先，创建初始人工鱼群。设定生成100条人工鱼，随机初始化个体位置。

然后，计算当前个体位置的目标函数值。比较“追尾或觅食或随机”和“聚群或觅食或随机”两种组合行为得到的下一位置目标函数值的大小，选取较优的一种行为来执行，从而确定搜索方向。同时采用随机移动步长，更新人工鱼位置，并计算更新后的目标函数值。待所有个体均完成移动后，将每次迭代得到的最优人工鱼位置及其对应的目标函数值存在bestx和besty。

最后，判断当前迭代次数加1后是否大于文中的最大迭代次数500，若大于则停止搜索，输出最优解；否则继续上述的迭代过程。

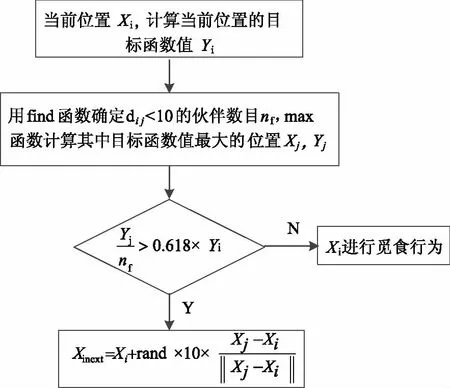
图3 第i条人工鱼的追尾行为

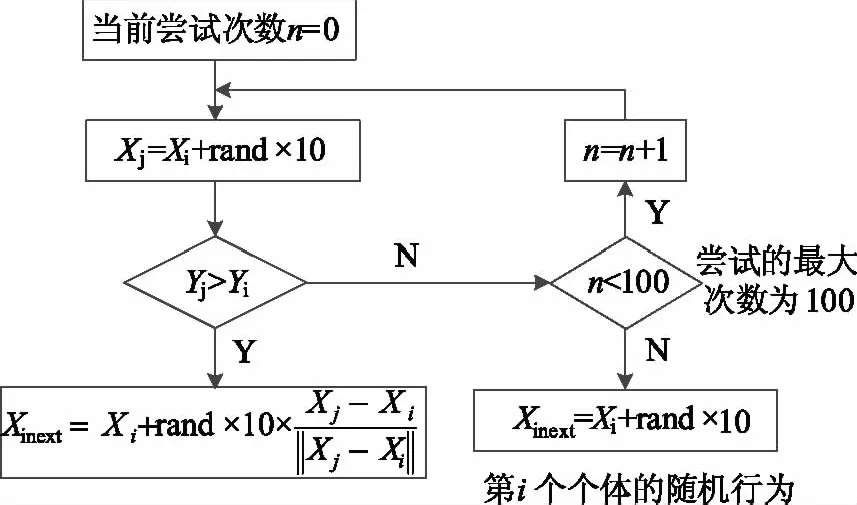
图4 第i条人工鱼的觅食行为

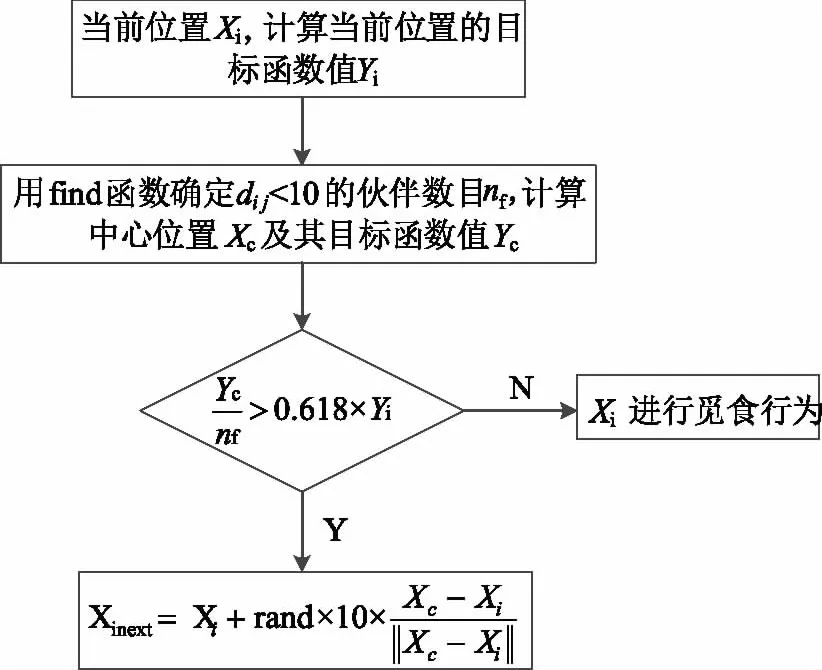
图5 第i条人工鱼的聚群行为

4 仿真结果及分析

为验证人工鱼群算法的有效性，在Matlab/ Simulink仿真环境中结合小型波浪发电系统的数学模型，运行了人工鱼群算法程序,如图6所示。主要参数为：浮子质量m=45 kg，附加质量mR=0 kg，辐射力阻尼系数RR=300 N·S/m，刚性系数Ks=800 N·S/m。

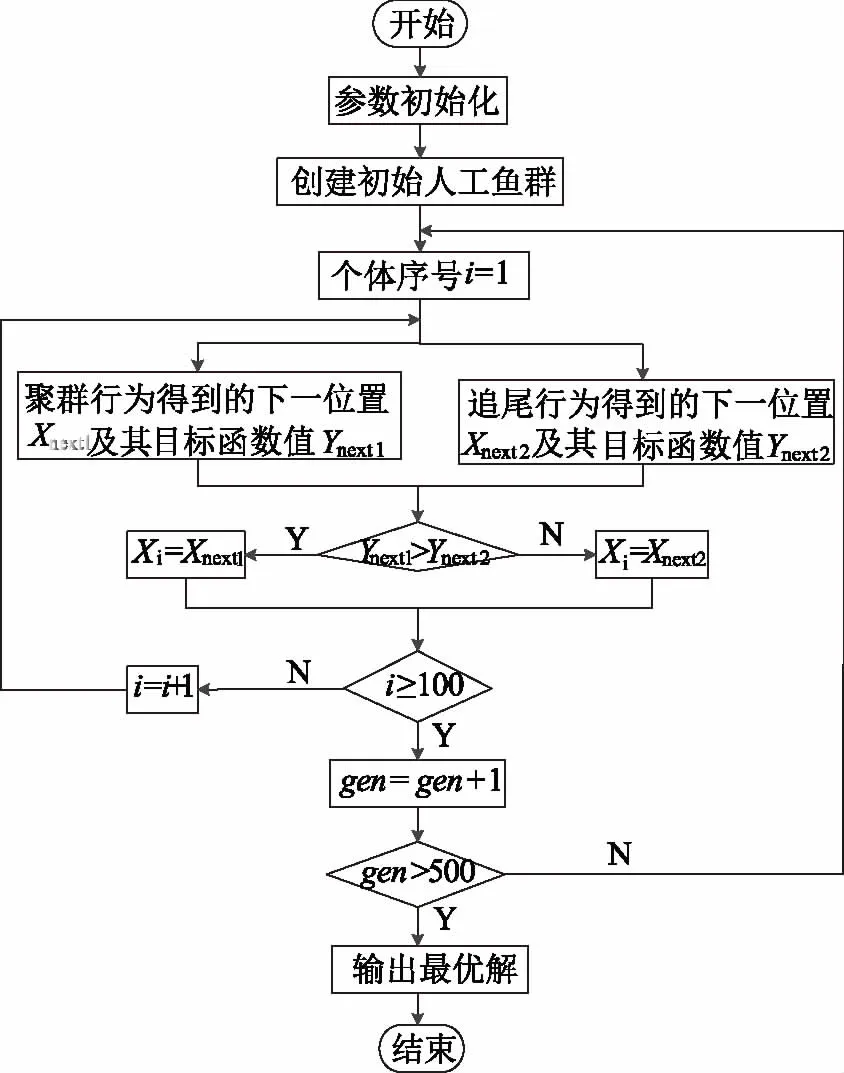
图6 人工鱼群算法的流程图

图7～图9分别是波浪周期T为5 s、6 s和7 s时，运行人工鱼群算法和传统粒子群算法的目标值优化过程，以图7为例进行说明。图7(a)为人工鱼群算法的优化过程曲线，图7(b)为鱼群算法迭代500次的最优人工鱼分布情况，图7(c)为传统粒子群算法的迭代过程。由图7(a)、图7 (b)的迭代次数可知，人工鱼群算法在迭代到第2代的时候，目标值已基本达到最优解，而传统粒子群算法需进化到第8代，始才逐渐稳定。因此，在成功寻优的迭代次数上，人工鱼群算法的寻优速度更快。

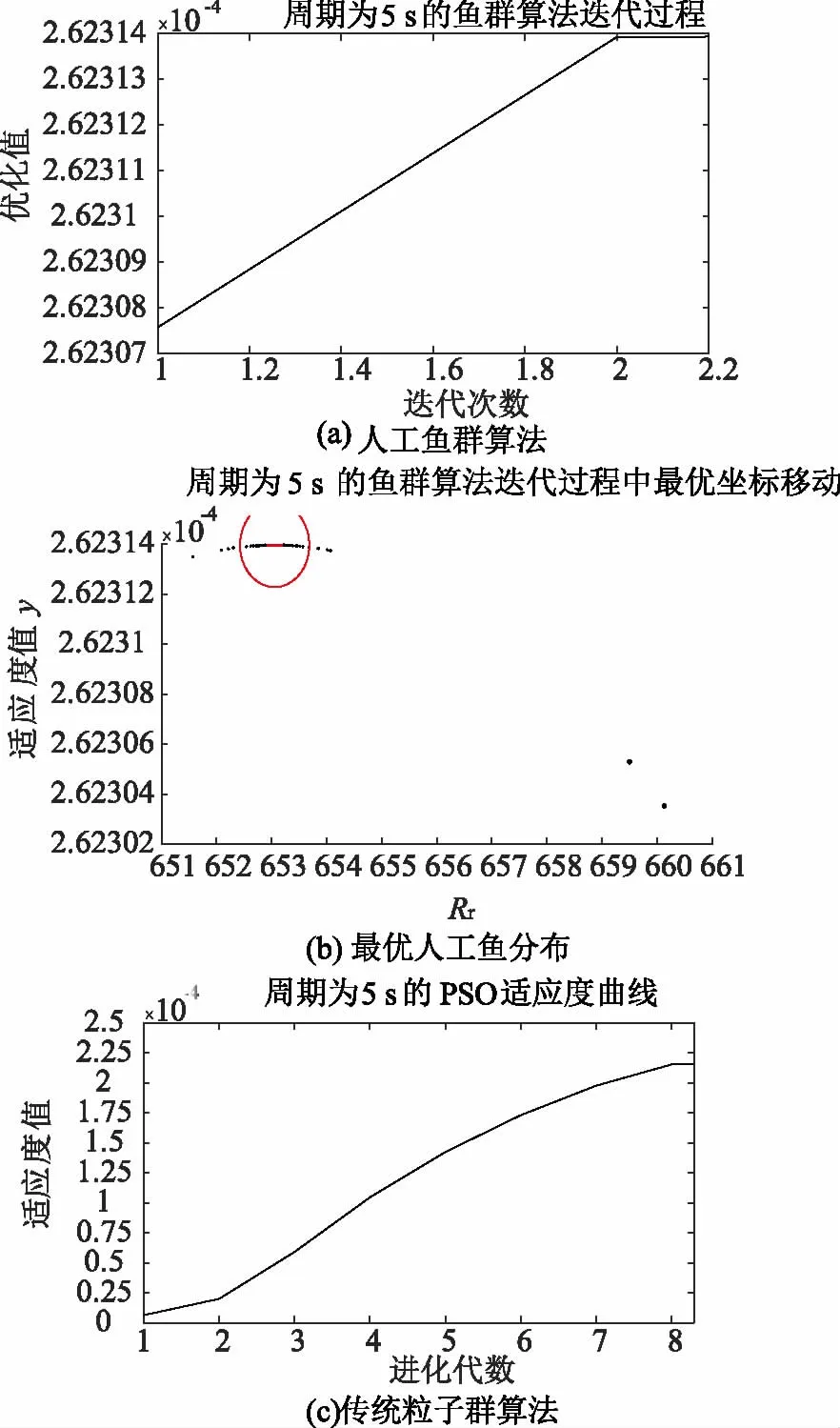
图7 周期为5 s时两种算法的目标值优化过程

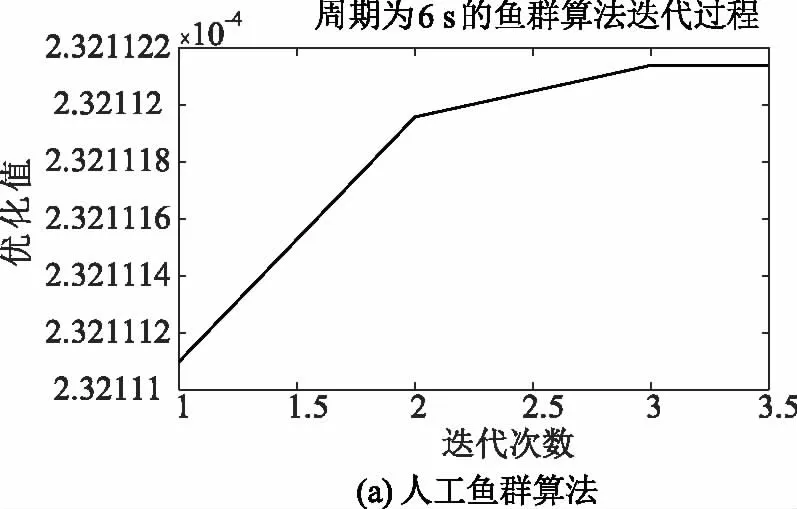
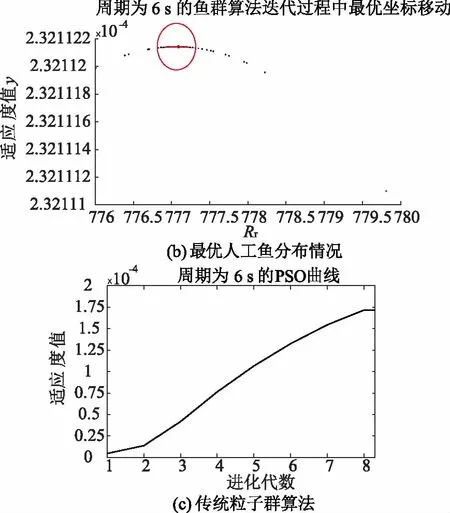
图8 周期为6 s时两种算法目标值的优化过程

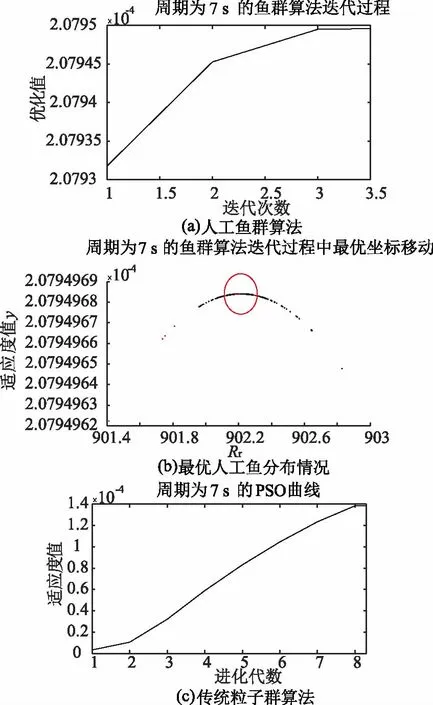
图9 周期为7 s时两种算法目标值的优化过程

表1和表2分别为采用人工鱼群算法和传统粒子群算法计算的目标值及与理论值的误差。由此可见，与传统粒子群算法相比，人工鱼群算法所计算的目标值基本与理论值相等，可大幅增加波浪发电系统的平均输出功率。

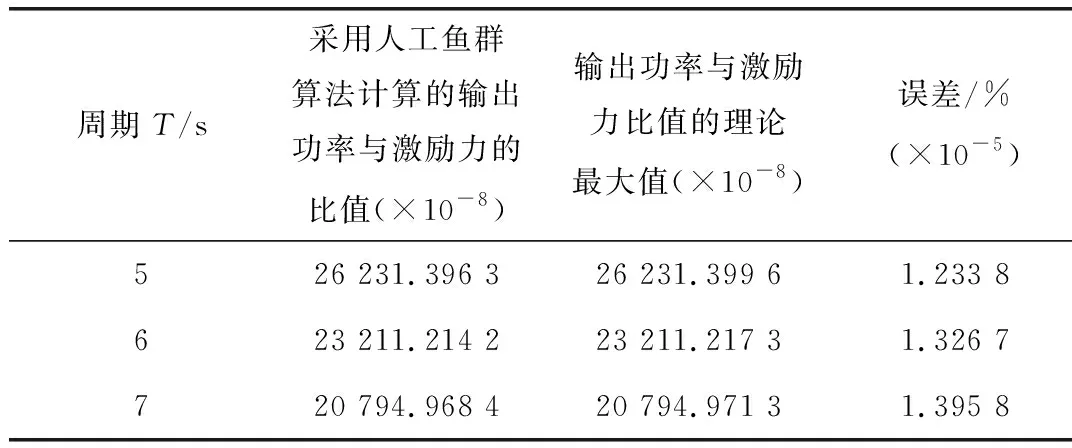
表1 采用人工鱼群算法计算的目标值

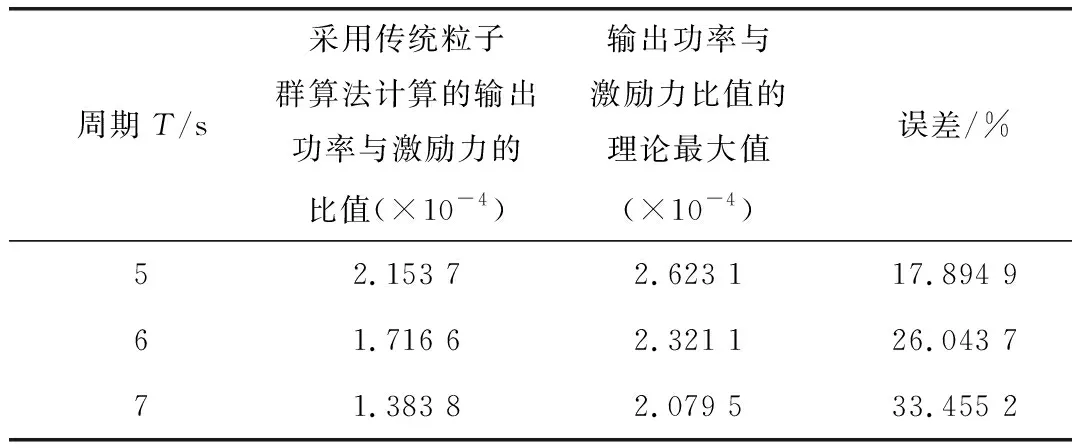
表2 采用传统粒子群算法计算的目标值

5 结束语

人工鱼群算法应用于寻找波浪发电系统的最优负载，可通过比较“追尾或觅食或随机”和“聚群或觅食或随机”两种组合行为得到的下一位置目标函数值的大小，选取较优的一种行为来执行，从而确定搜索方向，可避免陷入局部最优，提高算法全局搜索能力。通过加入随机移动步长，更新人工鱼位置并计算更新后的目标函数值，求解优化问题。仿真结果表明，与传统粒子群算法相比，所提算法寻优速度快，运行结果可达到理论最大值，获得全局最优解，大幅增加波浪发电系统平均输出功率，求解不同频率下系统最优负载。