一类微型扑翼飞行器的滑模自适应姿态控制*

李 航，何广平，毕富国

0 引 言

微型扑翼飞行器(flapping-wing micro air vehicle，FMAV)是一种基于仿生学原理，用于完成某些特殊任务的新概念飞行装置.根据空气动力学的研究表明，在小尺度下，扑翼飞行要优于固定翼和旋翼飞行器[1]，但系统结构更为复杂，外部动力需间接驱动和控制其飞行轨迹.对于各类飞行器来说，姿态控制是其完成精确定向、跟踪飞行至关重要的环节.整个姿态控制系统是一个复杂的非线性耦合的多输入多输出系统，由飞行器的执行机构产生力矩来完成[2].在其设计过程中普遍存在两类不确定性问题，分别是外界环境带来的干扰力矩，如制造缺陷、空气流动；由于飞行器的外形结构，惯性张量在多数情况下不能保证精确已知.

滑模变结构控制方法在应对非线性系统不确定性和抑制扰动中，具有良好的鲁棒性，可以获得较为理想的动态性能，在众多航空航天飞行器的鲁棒控制中得到广泛应用，如卫星[3-4]、四旋翼飞行器[5].但是，由于滑模控制需要知道系统不确定项的匹配条件，因此在不具备要求下设计的控制器会比较保守.同时为了使系统保持在滑动模态上，需要利用开关函数来进行逻辑切换，必然引起抖振现象，增加能量的消耗[6].为了弥补滑模控制的不足，本文引入自适应控制方法，来完成微型扑翼飞行器在悬停过程中调整方位的姿态控制.两者的结合一方面可以解决系统不确定项的匹配问题，抑制抖振；另一方面可以补偿自适应控制方法中，面对变化较快参数响应较慢的问题.

1 飞行器模型

1.1 坐标系和机翼运动轨迹

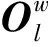
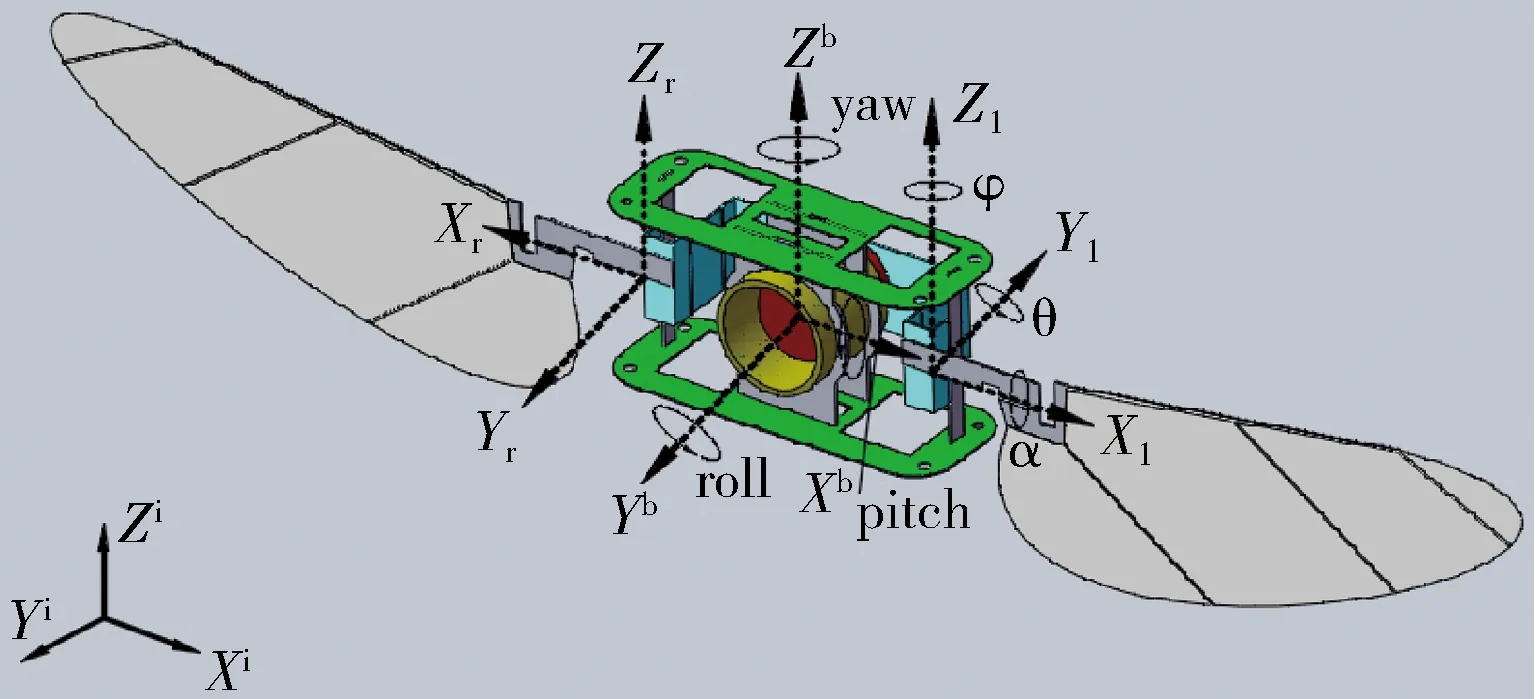
图1 微型扑翼飞行器的坐标系统Fig.1 Frames of FMAV

研究发现，一些生物仅用扑动和扭转便可以完成飞行过程[1]，因此本文忽略机翼挥摆运动，避免由其引起的尾流捕捉现象，导致系统模型的复杂化；并假设扭转发生在扑动的幅值处，且时间极端.

定义在坐标系Ow下机翼运动轨迹方程式(1)，如图2所示.

(1)

式中:φΔ为扑动中轴线偏移角度；φa为扑动角幅值；α0为扭转角幅值；sign()为符号函数；κ为一个周期T内，前(下)扑运动的时间占比.

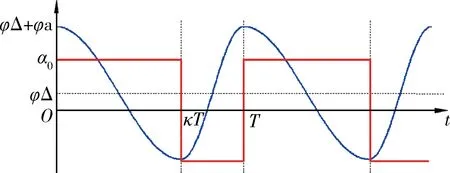
图2 机翼运动轨迹曲线(蓝φ红α)Fig.2 Wing angles configuration

1.2 气动力和力矩

FMAV能够在空中飞行，完成姿态的变换，依靠的是机翼之间不同运动轨迹所产生的气动力和力矩.对于扑翼在低雷诺数条件下的飞行机理，已有大量文献给予充分说明，在这里直接给出单个机翼所受瞬时升力fL和阻力fD的计算式[8]：

(2)

(3)

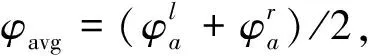
(4)

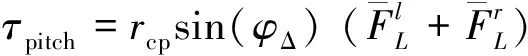
(5)

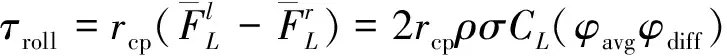
(6)

其中rcp为机翼根到机翼所受等效压力中心的距离，一般取0.6～0.7倍的翼展长度[11].偏航力矩不同于其他两个力矩，是由机翼的阻力在交替变化下引起的，如式(8).

(7)

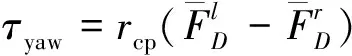
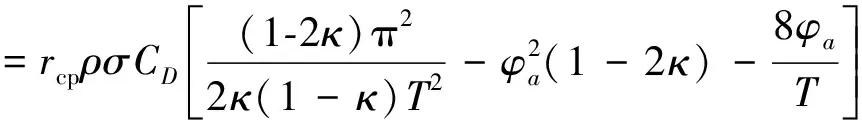
(8)

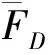
图3 力矩原理图Fig.3 Torque diagram

1.3 运动学和动力学模型

FMAV机翼的质量往往仅占总质量的2～3%，因此可以忽略掉双翼的惯性质量，而视系统模型为单一刚体.由于机体坐标系Ob与质心固联，那么定义坐标系Ob相对于惯性坐标系Oi的位置矢量P、旋转矩阵R，来表达飞行器的位姿：

P=[XYZ]T

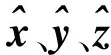
(9)

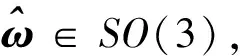
(10)

在坐标系Ob下，单一刚体动力学模型可以用牛顿—欧拉方程表达[7]为

(11)

其中I为单位矩阵；J为惯性张量；m为刚体质量.

(12)

其中c为粘滞阻尼系数；τ0为干扰力矩，导致其出现的主要因素为制造过程无法做到完全的轴对称以及气流的影响.将式(12)代入式(11)中，便可以得到飞行器的动力学模型：

(13)

其中g=[0 0g]T.

式(9)和式(13)便是飞行器的系统模型.不难看出，这个系统是包含12个变量的时变非线性系统,且气动力、力矩的变化呈现周期性.对于这种高频下的周期系统，平均化理论[12-13]可以有效地逼近实际模型，得到近似时不变系统.它已经被用于固定翼、扑翼飞行器以及航天器的模型建立过程中[13-15].结合力、力矩章节求解的平均参数，得到飞行器的平均模型：

(14)

2 控制器

本文希望在FMAV悬停的基础上，完成调整方位的稳定姿态控制，它与直升机、四旋翼飞行器的姿态控制过程有很多相似之处，是一类欠驱动控制问题，即4个输入(φl,φr,αl,αr)协调刚体空间的六个自由度.相对来说，四旋翼的姿态控制飞行有比较充分的发展进程，通过多种控制方式都已经具备了飞行能力.因此，针对FMAV的模型不确定性、非线性等问题，本文的控制方法将借鉴了四旋翼的研究成果[5]，采用滑模自适应控制来完成目标，如图4所示.

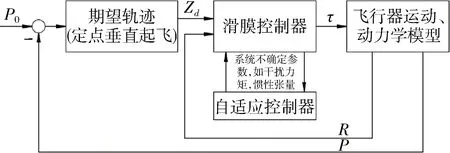
图4 飞行器姿态控制框图Fig.4 Block diagram of attitude controll

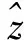
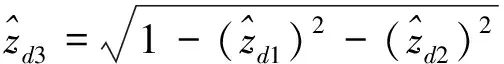
(15)

S=[s1s2s3]T=ωb+Ke

(16)

其中K=diag{k1,k2,k3}增益矩阵.

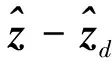
(17)

综上，定义滑模面姿态误差:

(18)

(19)

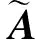
(20)

将式(14)、式(16)代入式(20)，得到

(21)

根据式(21)可以给出滑模控制的控制律为

(22)

(23)

(24)

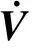
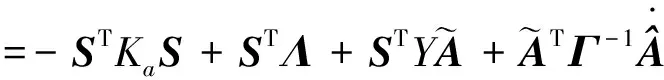
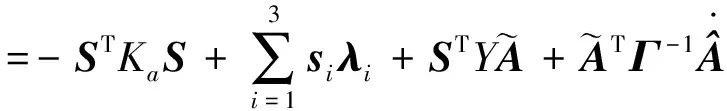
(25)

自适应律为

(26)

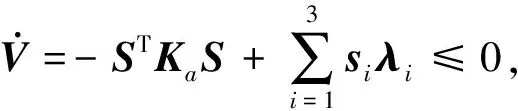
3 仿 真

为了验证本文所设计控制的有效性，本章节以一类带有被动扭转的微型扑翼飞行器为例，如图1，进行仿真分析，并对比控制器在有无自适应控制律下的性能.此类飞行器机翼的运动主要包括前后的扑动和由于气流反作用力而产生的被动扭转[17-19].

为了接近真实模型，采用式(13)作为仿真对象，但模型中角速度存在耦合现象，求解相对复杂.由于准稳态的运动过程，姿态的改变量是微小的，所以将导致耦合项远小于非耦合项[20]，例如(Jzz-Jyy)ωyωz与Jxxωx.因此将模型中角速度替换为ZYX欧拉角Θ=[γβη]T(机体坐标系Ob)表示，忽略掉耦合项，仅考虑主要的影响因素，结合式(9),得到下式(27)，以此作为仿真模型.

(27)

其中c=cos,s=sin.下面给出此飞行器和外部环境的参数：

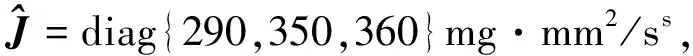
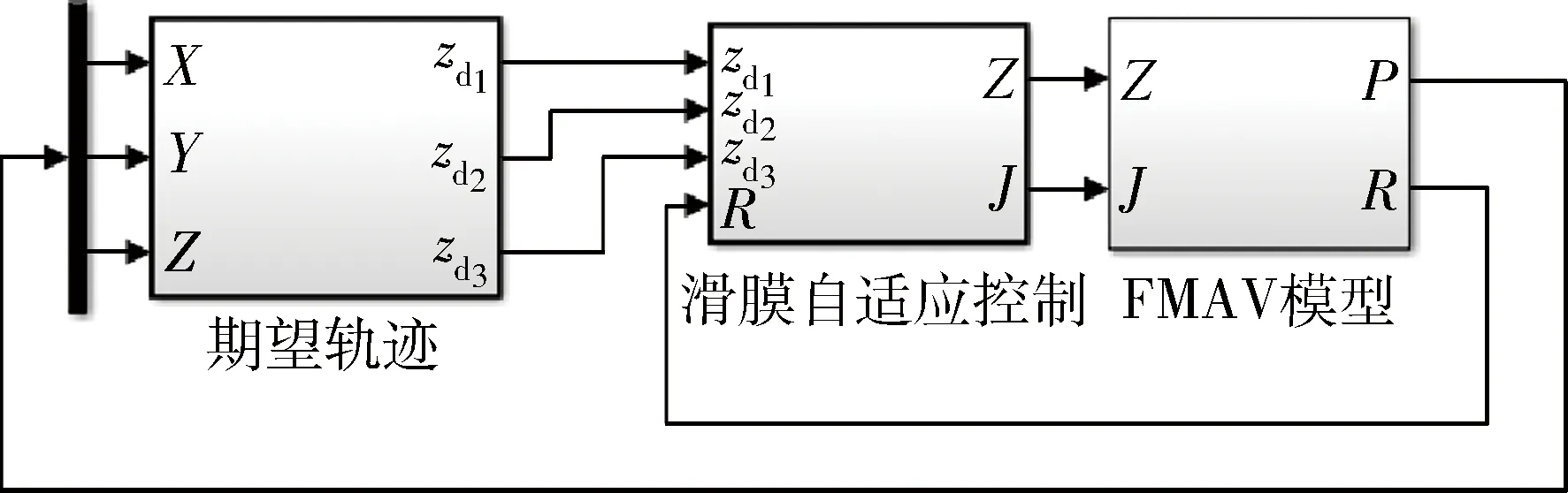
图5 Simulink仿真框图Fig.5 Block diagram of simulink

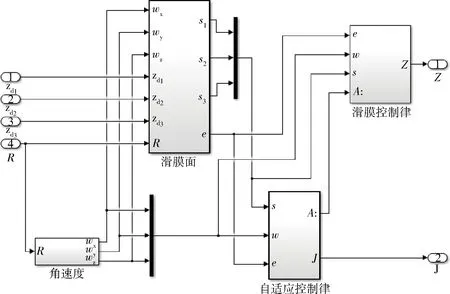
图6 “滑模自适应控制”子系统框图Fig.6 Sliding-mode adaptive attitude controller

图7～9为在没有干扰气流影响下FMAV的滑模自适应姿态控制过程，说明本文提出的滑模自适应控制方法，可以使此类飞行器在4 s内完成[0.1 0.1 0]T到[0 0 0]Tm的位姿稳定调整，满足上一章节提出的控制要求：图7为FMAV机翼运动控制量φl,φr的变化曲线；图7依次为飞行器姿态力矩τ变化曲线；图9为飞行器位姿P、Θ的变化曲线.

接下来，在上述仿真结果的前提下，沿Yb轴对FMAV施加正弦变化的干扰气流0.001sin(10t)，得到图10～12：其中图10为在干扰气流下飞行器位姿P、Θ的变化曲线；图11为俯仰力矩的变化曲线.从图中可以看出飞行器在微小幅度的修正姿态，稳定于期望附近，以此证明系统具有良好的抗干扰能力.

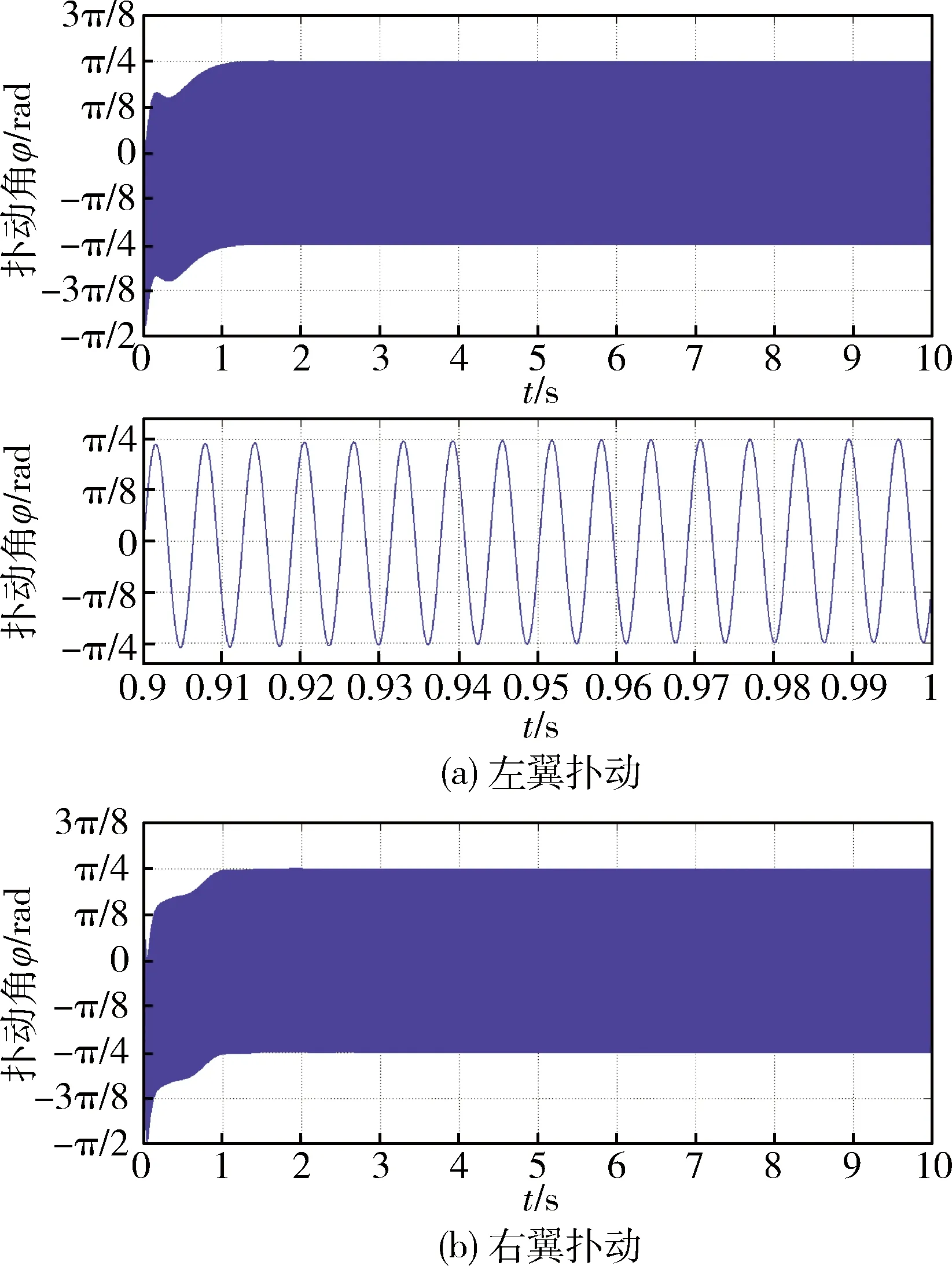
图7 运动控制量变化曲线Fig.7 Stroke angle

图8 输出力矩变化曲线Fig.8 Torque output

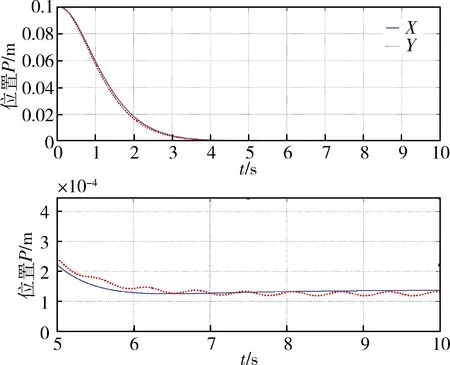
图10 飞行器位置P变化曲线(有干扰气流)Fig.10 Position tracking under the sinusoidal interference

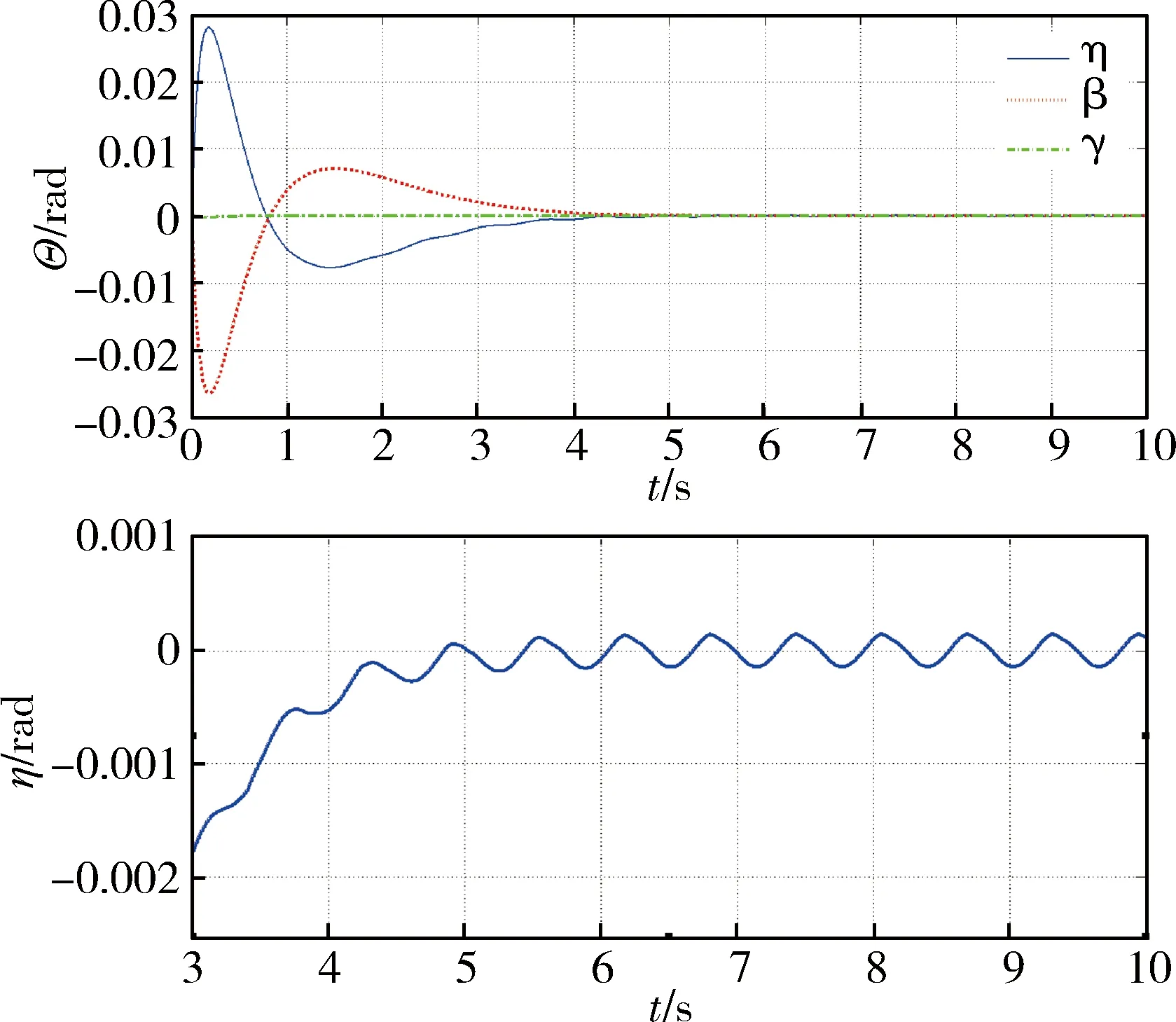
图11 飞行器欧拉角Θ变化曲线(有干扰气流)Fig.11 Euler angle tracking under the sinusoidal interference

图12 输出俯仰力矩τpitch变化曲线 (有干扰气流)Fig.12 Pitch torque output under the sinusoidal interference

最后通过去掉自适应控制律式(26)，仿真得到图13俯仰力矩τpitch在有、无自适应控制下的变化曲线.在存在自适应律的滑模控制中，抖振问题得到有效改善，避免输出高频现象，从而保护这个系统.

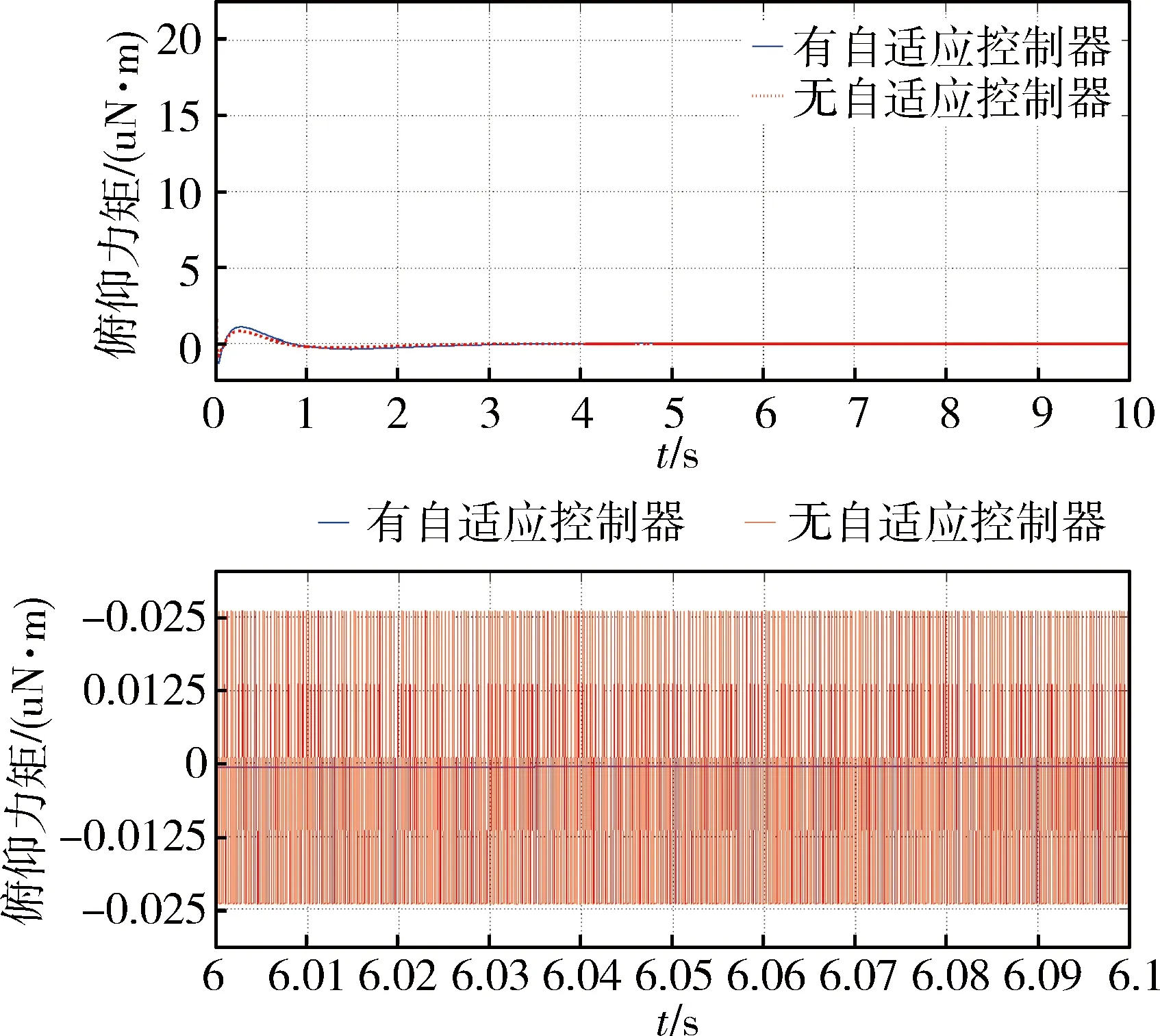
图13 自适应律对滑模控制的影响Fig.13 The influence of adaptive law on sliding mode control

4 结 论

微型扑翼飞行器的姿态控制系统是一类MIMO非线性不确定系统.针对这类系统，本文提出了滑模自适应控制算法.根据FMAV系统模型的二时间尺度特性，采用平均化处理模型，得到近似时不变系统.通过自适应规则来估计系统无法确定的计算参数——干扰力矩和惯性张量，用滑模控制消除系统的跟踪误差，二者的结合也有效的避免了抖振现象.仿真结果表明，所设计的控制系统在外界干扰下有良好的鲁棒性，提高了微型扑翼飞行器的姿态控制性质.