一种基于控制参数化的双连杆机械臂最优PID参数整定方法*

郭小龙，郭敏华，谭 元，曹函宇，佃松宜，李 彬

0 引 言

随着社会生产的不断扩大，可靠、高效的机械臂在工业、安全防爆等重复和危险的领域有不可代替的作用.由于任务差异，需要根据实际应用规划机械臂运动轨迹，来完成机械臂末端的位置和姿势，因此对机械臂关节实施精确快速控制就显得尤为重要.通过给定各关节的驱动力矩，使得机械臂各关节的位置、速度等状态变量跟踪给定的期望轨迹,即为刚性机械臂关节空间轨迹跟踪问题.大部分应用的机械臂是一个多输入多输出的强非线性系统，在工程应用中存在干扰不确定性、动态建模不完善以及参数的摄动，使得对机械臂的控制有一定复杂性.根据机械臂的这些性质，应用机械臂的控制方法主要有[1]：PID控制；自适应控制；鲁棒控制；神经网络控制和模糊控制；迭代学习控制.虽然提出方法很多，可在工程控制中PID控制算法和改进型依然有90%以上的使用率[2]，而PID控制最核心的工作是要整定比例积分和微分的前项参数使得系统的动态和静态性能指标得到满足甚至使某指标达到最优，因此本文将探讨一种新型的最优PID参数的整定问题.

PID参数整定的方法较多，可以将这些方法分为常规整定法和智能参数整定法两类.常规PID整定方法在文献[3]中最早提出，现在已经有很多改进方法和新的整定方法，通过系统特征[4-6]或者继电反馈[7-8]等方法来达到整定参数的目的.智能整定方法是由Astrom在1988年提出的[9],主要可以分两种，分别为基于模型和基于规则两种.前者是根据系统模型是基于Z-N法的改进，通过对输入输出的识别整定参数[10-11].后者则不要知晓系统模型[12-13]，基于类似于有经验的操作者手动整定的规则，基于规则使用暂态响应、设定值改变、负载和干扰的变化等来达到整定参数的目的[14-15].

本文对于双连杆机械臂提出一种基于控制参数化的最优PID整定方法.此方法主要如下所述：首先将系统的上升时间、超调量、响应时间等性能指标和工程应用中物理约束如关节电机驱动力矩建模为最优控制中的连续状态不等式约束.如此，双连杆机械臂的最优PID参数整定问题转化为含连续状态不等式约束的最优参数选择问题.因为每个点的约束都需要被满足，导致每个约束要满足无穷多个约束，所以连续状态不等式约束十分棘手，这类问题在数学规划中被称为半无限规划[16].处理这种约束有很多种方法，其中代表性的方法有约束转录法[17-22]和精确罚函数法[16，23].在本文中应用约束转录法与局部平滑法相结合来处理连续状态不等式约束.经过这样的处理，原约束变为一个标准约束的形式[17].同时，问题的可行域会随之发生变化，通过文献[17]中所提出的渐近调整相关参数的方法来解决，且此算法已经嵌入在最优控制计算软件MISER 3.2中.经过本文方法的处理得到一个标准的最优参数选择问题，直接能用MISER 3.2来求解此问题[25]，也可以用文献[24]中提出新的fortran版本求解.由于本文的方法是基于梯度来进行求解，所以需要代价函数和变换后约束的梯度公式.为此，本文给出了这些梯度计算公式以及推导过程.最后，不借助于简化和线性化，通过本文提出的方法得到了一个最优PID控制器，通过对机械臂位置跟踪问题的数值仿真，其结果表明，该方法能有效地达到控制系统运行所要求的性能,从而验证了本文所提出的方法是有效的.

1 双连杆机械臂的模型和问题描述

本文的目标是设计一个PID控制器使臂杆能始终跟踪期望轨迹，从而完成相应的动作.考虑一个双关节机械臂，其动力学方程为[1]

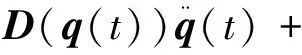
(1)

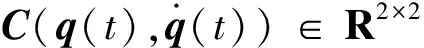
(2)

式中，k1和k4，k2和k5，k3和k6分别为两个电机的控制输入的比例、积分和微分的增益，e(t)=q(t)-qd∈R2,e(t)=[e1(t)e2(t)]T,t∈[0，T],qd为期望角度,其中T=5s.设

则双关节机械臂的动力学方程为

(3)

式中,c11=c12=-m3sinx3(t),c21=-c11,G(q(t))=[φ1(t)φ2(t)]T，d21=d12,g2=m5gcos(x1(t)+x3(t))，w=d22d11-d21d12,d11=m1+m2+2m3cos(x3(t)),d12=m2+m3cos(x3(t)),d22=m2，

g1=m4gcos(x1(t))+m5gcos(x1(t)+x3(t))，

式(3)中mi(i=1,2,…,5)的值由式m=P+pll给出[1],pl为负载,P为机械手自身的参数向量.

x(0)=[0 0 0 0]T

(4)

在实际应用中，为了限制超调引入如下约束：

g1(t)=x1(t)-105%qd1≤0,t∈[0,5s]

(5)

g2(t)=x3(t)-115%qd2≤0,t∈[0,5s]

(6)

式(5)～(6)表示机械臂的两个连杆的响应不能超过各自参考输入qd1,qd2的5%和15%.

基于上升时间、调整时间和稳态误差等性能要求，引入如下约束：

g3(t)=h1(t)-x1(t)≤0,t∈[0,5]

(7)

g4(t)=h2(t)-x3(t)≤0,t∈[0,5]

(8)

式中

式(7)～(8)表示两臂在1 s内必须达到参考输入的80%，在第2 s内必须达到参考输入的98%，满足稳态误差在0.02qd内.

考虑双连杆机械臂两个电机的输出功率物理限制，引入如下约束：

g5(t)=u1(t)-150≤0,t∈[0,5]

(9)

g6(t)=u2(t)-15≤0,t∈[0,5]

(10)

式(9)～(10)代表臂1的控制输入必须在150内，臂2的控制输入必须在15内.

根据跟踪参考信号qd1和qd2,可得到系统的代价函数为

(11)

对于式(2)中给定的积分项，引入新的状态变量

(12)

(13)

于是根据式(12)～(13)将状态方程(3)转换为式(14)

(14)

PID控制器为：

(15)

式中ki,i=1,2,…,6在式(2)中给出，分别为PID的比例、积分和微分的增益.

本文考虑的PID参数整定问题可以描述为：给定系统(14)，求其PID控制参数ki使代价函数(11)最小且满足于连续状态不等式约束(5)～(10)，这个问题被记做问题P.显然，问题P是一个最优参数选择问题.

2 连续状态不等式约束函数的转化和计算方法

求解连续状态不等式约束(5)～(10)十分棘手，是因为每一个约束都包含无限多个约束条件.在这里，应用约束转录法结合一种局部光滑的方法来处理[18,19,20,21,25].首先，将连续状态不等式约束(5)～(10)等效为如下的等式约束：

(16)

然而，式(16)中的max{gi(t),0}不可微，因此,对于每个i=1,2，…,6都用光滑函数Li,ε(t)来近似.即

(17)

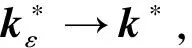
式(17)中给出的ε>0为可调常数，故式(17)可微，但是式(17)的可行域与式(16)的不同，因此应用中提出的参数调整渐近的方法来解决[19].具体而言，对于每一个i=1,2,…,6,设

(18)

将问题P中的(5～10)用式(18)替换后得到问题Pε.

若用数值法求解问题Pε,得到的最优解就不满足式(18)的约束规范.于是，引入如下等式：

我院2005－2017年嗜麦芽窄食单胞菌的临床分布及耐药性分析 …………………………………………… 熊丽蓉等（16）：2248

(19)

将问题P中的(5～10)用(19)替换后得到问题Pε,γ.其证明类似文献[19]中的定理8.3.1.

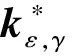
(20)

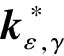
根据定理1和定理2，给出如下算法来近似地求解问题P.

算法3.对于任意ε>0,γ>0.在此问题中取ε=10-1，γ=5ε/16,εmin=10-3.

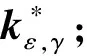
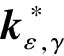
第4步：令γ=γ/2,转至第1步；

第5步：令ε=ε/10,γ=γ/10,转至第第一步；

当ε≤εmin时，算法停止.

备注1.由于双连杆机械臂控制问题为非线性问题，单一的PID参数在不同初始条件下难以满足系统所有的性能和条件约束.所以，对于不同范围的初始条件可用文中的方法整定出相应满足约束的PID参数.然后在实际应用中对于不同的初始条件可切换相应的控制参数使其满足特定的性能和条件约束.

3 代价函数和约束的梯度公式

在本节中，提出一种通过代价函数和连续状态不等式约束对k的梯度求解问题Pε,γ，从而求解原问题P的计算方法.为了求解每一个k对应的代价函数和连续状态不等式约束得梯度，给出以下两个定理.其证明均类似文献[19]中的定理5.2.1.

定理3.代价函数的梯度公式为

(21)

式中H0(t,x(t),k,λ0(t))为哈密尔顿函数，

H0(t,x(t),k,λ0(t))=

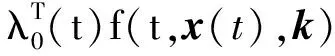
(22)

f为动力学方程(14)的右端项，λi(t)方程(23)的解

(23)

其边界条件为

λ0(T)=0

(24)

定理4.连续状态不等式约束函数的梯度公式为

i=1,2,…,6

(25)

式中Hi(t,x(t),k,λi(t))为哈密尔顿函数

Hi(t,x(t),k,λi(t))=

(26)

f为动力学方程(14)的右端项，λi(t)为方程(27)的解

(27)

式中i=1,2,…,6,其边界条件为

λi(T)=0,i=1,2,…,6

(28)

利用基于梯度(定理3、定理4)的优化方法，如序列二次规划逼近方案[19],可将这些最优参数选择问题转换为一个非线性优化问题求解.因此，可用最优控制软件MISER 3.2计算.

4 计算结果与仿真

本节中使用刚性双连杆机械臂的位置跟踪问题，验证算法的有效性，跟踪信号为阶跃信号.具体参数如下，在计算中选取关节1和关节2 的长度分别为l1=l2=1.在笛卡尔空间中的理想跟踪信号取qd1=qd2=1.机械臂自身的参数向量P=[1.66 0.42 0.63 3.75 1.25]T,pl=0.50.代入本文提出的PID整定算法，计算得到：

k1=47.8,k2=0.95,k3=30,

k4=15,k5=0.24,k6=4.6.

根据参数进行了两次仿真，初始条件为x1=x2=x3=x4=0,分别为无干扰和有干扰的情况，得到响应曲线和两个电机力矩的输出情况，如图1和图2所示.

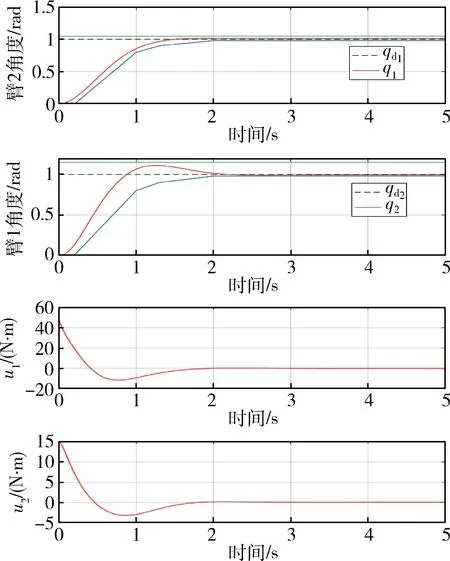
图1 无干扰时臂1和臂2的响应曲线和控制输入Fig.1 Response curves and control inputs of link 1 and link 2 without disturbance

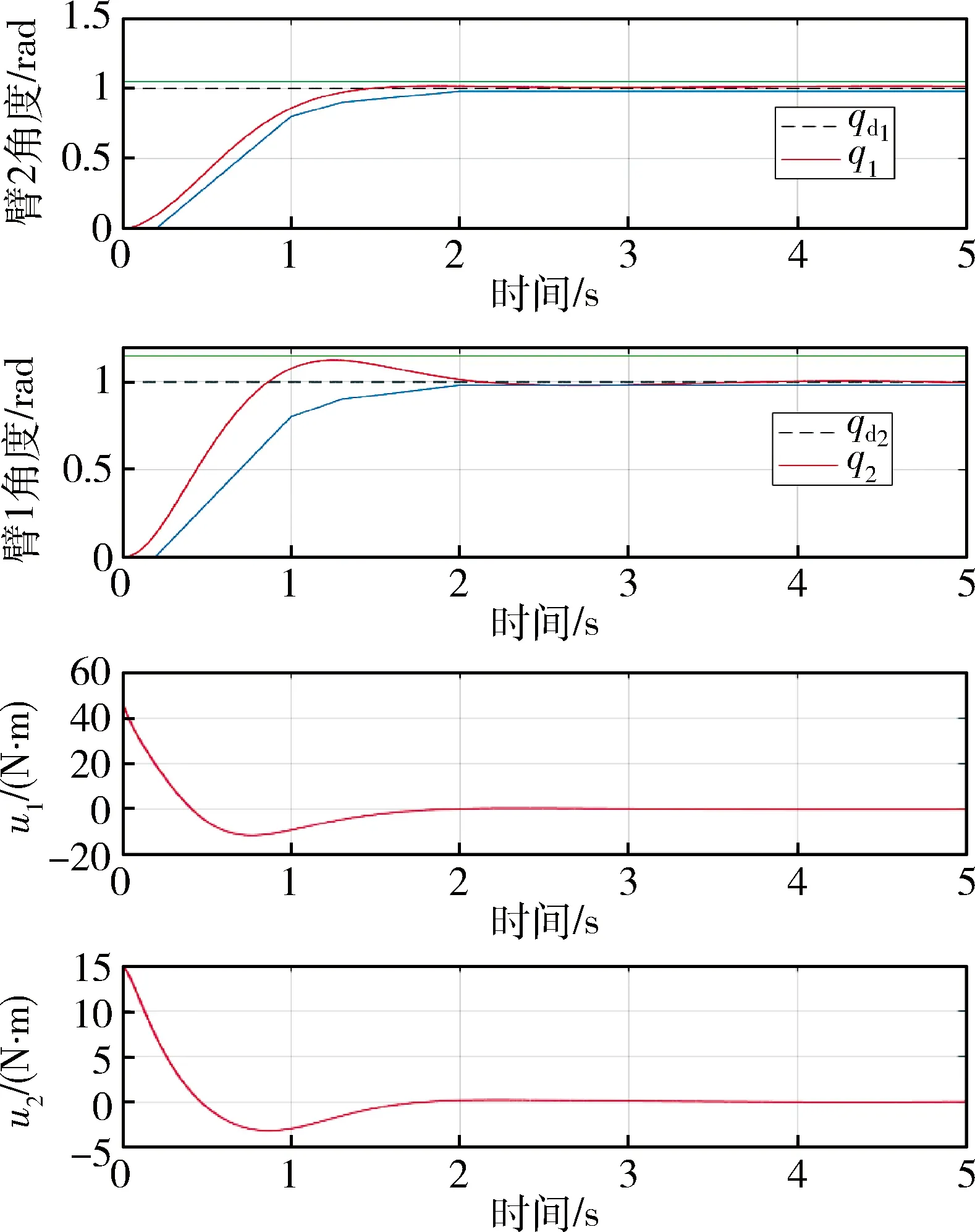
图2 有干扰时臂1和臂2的响应曲线和控制输入Fig.2 Response curves and control inputs of link 1 and link 2 with disturbance

如图1所示.臂1和臂2在输入激励信号以后，响应曲线在1 s内都达到了参考输入的80%，且分别在第1.3 s和第1.9 s达到稳态，满足了约束g3(t),g4(t).臂1和臂2的超调分别小于105%和115%满足了g1(t),g2(t).控制输入最大时分别为43和15满足约束g5(t),g6(t)的要求，且在没有其它输入时保持一个稳定值.由结果可知，所有的约束条件都得到了满足.

为了测试该PID控制的抗干扰能力，在仿真时加入正弦干扰信号，结果如图2所示.系统的响应曲线基本满足所有约束，同时控制输入的约束也得到满足.此外，两臂的位置曲线相比图1有一些振动，但经过小幅度地振动后稳定误差都在0.02qd以内.因此，通过第二个仿真实验，可证明所设计的双连杆机械臂最优PID控制方法具有一定的抗干扰能力.

5 结 论

本文提出了一种基于控制参数化的双连杆机械臂最优PID参数整定方法，考虑性能的要求和工程实际的约束，使用本文提出的整定方法得到具体控制参数.通过数值仿真结果表明本文提出的机械臂最优PID参数整定方法有效性和可靠性.尽管现在许多先进的控制方法在理论上可以对此问题进行比较精确的控制，但是由于其复杂性和不易实现性限制了其更大化的应用.相反，PID控制计算实现都较为简单，可以实现较好性能，且具有一定抗干扰性，所以相比现有方法本文提出算法具有较大的使用价值.