巧借几何直观 妙解中考试题——对一道中考试题的解法探析

☉湖北省宜昌市第九中学 窦正安

几何综合题是初中阶段很多学生难以逾越的一大难题.究其原因，无非在于很多几何综合题需要学生具有较强的逻辑推理能力、计算能力，甚至需要借助转化或添加辅助线.在众多的题目中，那些基于核心素养的，具备一题多解的，甚至拥有拓展空间的好题常被人津津乐道.笔者从众多中考试题中撷取一例加以剖析，以飨读者.

题目：（2018·湖北宜昌）如图1，在矩形ABCD中，AB=12，P是边AB上一点，把△PBC沿直线PC折叠，顶点B的对应点是点G，过点B作BE⊥CG，垂足为E且在AD上，BE交PC于点F.

（1）若点E是AD的中点，求证：△AEB △DEC；

（2）①求证：BP=BF；

②当AD=25，且AE＜DE时，求cos∠PCB的值；

③当BP=9时，求BE·EF的值.

由于（1）、（2）①和②较为容易，过程从略.以下重点探析（2）③的解法.

解法1：如图1.

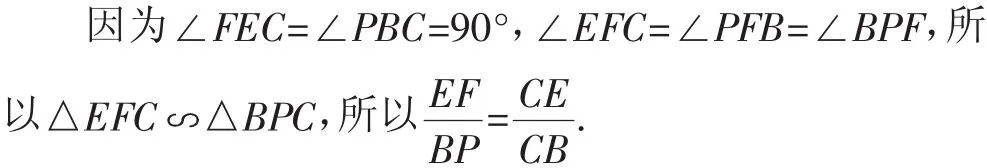
由AD∥BC，得∠AEB=∠EBC.又因为∠BEC=∠A=90°，所以△AEB △EBC，所

所以BE·EF=AB·BP=12×9=108.

点评：此解法的出发点是根据目标联想到了相似，通过两次相似构建包含目标线段的比例式，再转化为等积式求得结果.其优点在于思路比较清晰，易于想到运用相似，缺点是图中不止两对相似三角形，如果选择偏差就很难得出能求出结果的比例式.事实上，我们在阅卷的过程中也的确发现有不少学生想到用相似，但由于选择不当，如证△EFC △GPC，又没想到等量代换，最终只能望题兴叹.

图1

解法2：如图1，设AE=y，EF=x，则BE=x+9.

易证△BAE △EDC.

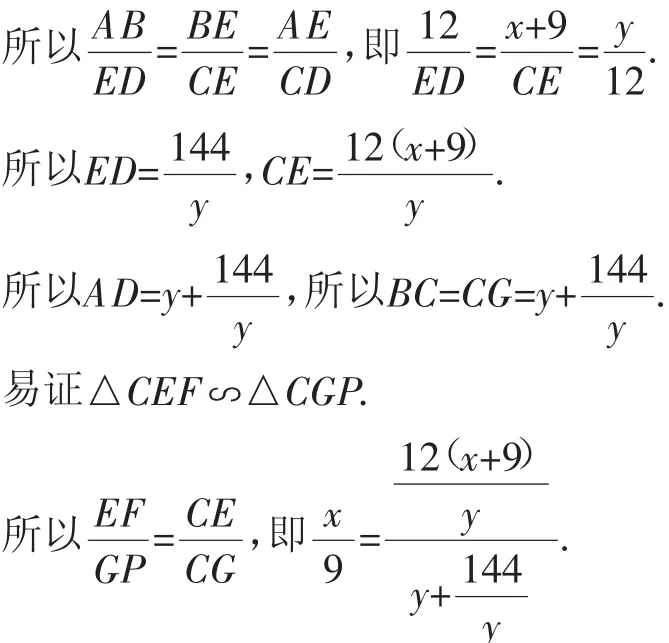
化简得：x（y2+144）=108（x+9）.

在Rt△BAE中，（x+9）2=y2+144.

所以x（x+9）2=108（x+9）.

又因为x+9≠0，所以x（x+9）=108.

所以BE·EF=x（x+9）=108.

点评：此解法的思路是运用设元法，先表示出目标线段和所需线段，再根据相似和勾股定理列方程解决问题.其优点在于思维比较简单、直接，缺点在于计算较为烦琐.事实上，在阅卷中，我们也发现了运用此法的学生，但最终绝大多数人都是因为计算问题而搁浅，甚至发现少数计算能力较强的学生本已算到x（x+9）=108这一步了，却选择把x解出来，没有运用整体思想，无形中增加了计算量，着实令人唏嘘..

解法3：如图2.

设EF=x，则BE=x+9.

过点F作FH⊥BC，垂足为H.

因为EF⊥CE且∠ECF=∠HCF，所以FH=EF=x.

易证△BAE △FHB.

所以x（x+9）=108，所以BE·EF=x（x+9）=108.

点评：此解法充分借助图形的几何直观性，由折叠的性质得知CP平分∠BCG，所谓“图中有角平分线，常向两边作垂线”，故过点F作FH⊥BC构造辅助线，此解法较解法2大大减少了计算量.

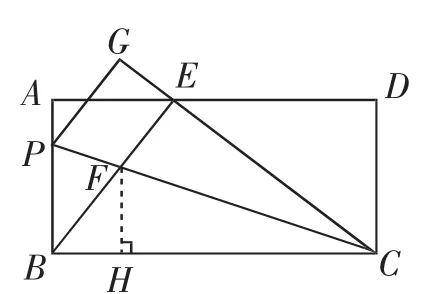
图2

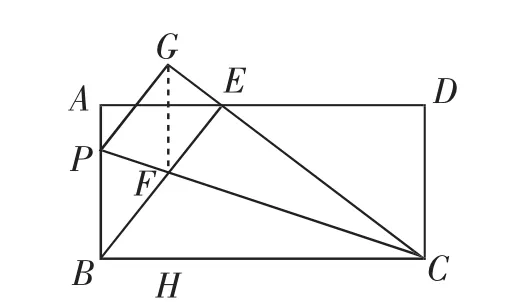
图3

解法4：如图3.

连接GF.

因为∠GEF=90°，∠PGE=∠ABC=90°，所以∠GEF=∠PGE.

易得BF∥PG，BF=PG，所以四边形BPGF是平行四边形.

又因为BP=BF，所以平行四边形BPGF是菱形.

由BP∥GF，得∠GFE=∠ABE.

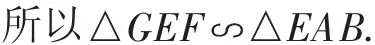
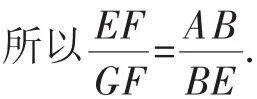
所以BE·EF=AB·GF=12×9=108.

点评：此解法充分地抓住了图形的几何直观性，即局部对称性.由折叠知△BPC与△GPC关于直线CP对称，于是想到“沿轴将图对折看，对折之后关系现”，FB对折后应该与FG对应，故而想到连接GF.与此同时，通过对折我们也不难发现：图中缺少EF的对应线段，这样想来就把解法3、解法4贯通起来了.正所谓：“图中有角平分线，常向两边作垂线.沿轴将图对折看，对折之后关系现”.