高等数学中应用微积分证明不等式的探讨

霍奴梅

(吕梁学院汾阳师范分校，山西 汾阳 032200)

0 引言

高等数学不等式解题存在一定困难已经成为共性问题，不等式为高等数学中的重要部分，在其中占据重要作用。在对不等式进行证明的过程中，模式存在不固定性，会由于题目的差异，产生不同的解题方法，具有较高灵活性，微积分证明不等式对高等数学的发展具有重要意义，应当对此进行深入研究，为高等数学发展做出贡献。

1 函数最小值、最大值、极值证明不等式方法

利用函数解不等式，这种方法属于解不等式的常规方法，在解题过程中一般都会选择此种方式，这种方式可以利用最大值、最小值和极值根据已知条件直接求值，需要找到其中的切入点，将函数值进行对比即可。

1.1 最小值、最大值解题方式

1)对闭区间[a，b]的连续函数最大值、最小值求解：需将其中可疑点解出，再将两个端点a、b以及可疑点部分函数值进行对比，数值大的为最大值，相反则为最小值。

2)对开区间[a，b]可导函数最大值、最小值求解：设定f(x)在(a，b)中可导，并且极端为唯一值，所存在的极值点便是最大值点或者最小值点。

1.2 可导函数单调性解不等式

可导函数证明不等式的方法是利用导数符号与函数单调性关系求解的，这种解题方法以及解题过程如下：

例如f(x)，g(x)可导，证明f(x)>g(x)。

证明：首先利用减法，假如x>a，可以转换证明f(x)-g(x)>0。在此结构中辅助函数F(x)=f(x)-g(x)，假如F′(x)>0，F(a)=0，那么F(x)单调函数则呈现递增趋势，因此，F(x)>F(a)=0，F(x)=f(x)-g(x)>0。那么f(x)>g(x)，假如F′(x)不可作为判断大于0的数值，F′(a)=0，则计算F″(x)，假如F″(x)>0，那么F′(x)则呈现单调递增趋势，那么F′(x)>F″(a)=0，F(x)为单调递增趋势，从而得出F(x)>F(a)=0，因此f(x)>g(x)。

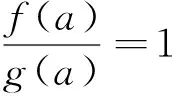
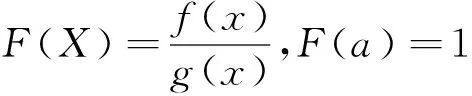
φ′(x)=f″(x)g(x)+f′(x)g′(x)g″(x)-f(x)g″(x)-f(x)g′(x)，

φ′(x)=f″(x)g(x)-f(x)g″(x)。

1)假如φ′(x)>0，F(a)=1，φ(a)=0，那么φ(x)则呈现单调递增趋势，F′(x)>0，那么F(x)呈现单调递增。在此过程中F(x)>F(a)=1，从而得出f(x)>g(x)。

2)φ′(x)<0，F(b)=1，φ(a)=0，那么φ(x)呈现单调递减趋势，F′(x)<0，便会存在F(x)单调递减趋势，并且此过程中F(x)>F(b)=1，那么f(x)>g(x)。

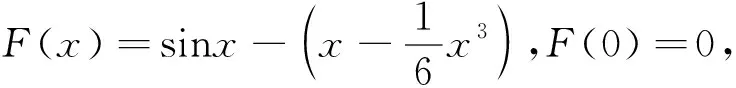
在本次解题过程中，F′(x)无法判断出是否大于0，但是两端点数值为0，因此求F″(x)，F″(x)依旧不能判断是否大于0，但是F″(0)=0，继续求F‴(x)，F‴(x)>0，并且所采取极值点为0，在一步步推理后可以计算出F″(x)，F′(x)，F(x)呈单调递增趋势，便能够呈现单调递增趋势，可得出最终结论，此次解题过程可利用定积分方法求解。

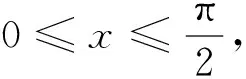
在此解题过程中可以发现，利用函数单调性进行求解，不等式两边函数可导，并且结构辅助函数F(x)需要在闭区间中连续，开区间内可导，并且在闭区间某端点f(x)数值为0，根据开区间中F′(x)符号判定F(x)在闭区间的单调性。首先可利用减法，若减法不能成立，并能够满足除法条件，便能够利用除法解题。

2 导数定义证明不等式的方式

导数解不等式的方法能够利用条件进行假设，将问题转化然后进行解析，属于解不等式中的简单技巧。

例3 假设函数f(x)=a1sinx+a2sin2x+…+ansinx，其中a1，a2，…，an为实数，n在其中代表正整数，已知条件为实数x，并存在|f(x)|≤|sinx|，证明：|a1+2a2+…+nan|≤1。

解析：在此问题中存在条件与结论不为同一类型的函数的问题，需对其中条件关系作出详细分析，通过分析能够发现：a1+2a2+…+nan=f′(0)。因此可以将问题转化为解析|f′(0)|≤1。

证明：f′(x)=a1cosx+2a2cos2x+…+nancosnx，得出f′(0)=a1+2a2…+nan。

因为：|f(x)|≤|sinx|

可以得出a1+2a2+…+nan≤1。

经过本次计算可以说明利用导数定义解决不等式问题的应用范围并不大，解题过程较为复杂，必须仔细探讨问题与条件的关系，才能得出结论。

3 应用拉格朗日中值定理解析不等式

3.1 拉格朗日中值定理

3.2 拉格朗日中值定理解析理念

拉格朗日中值定理存在形式为等式，那么采取哪种方式利用定理证明不等式，在拉格朗日中值计算过程中ξ∈(a，b)，可根据ξ在(a，b)取值范围评估f′(ξ)取值范围，构建不等式。

3.3 利用拉格朗日中值定理解析不等式步骤

1)验证函数在区间中能够满足拉格朗日中定理的条件，并设定自变量取值区间为[a，b]。

3)若ξ取值范围为f′(ξ)的范围，可以验证不等式。

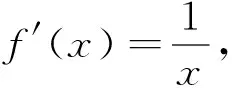
说明：拉格朗日中值定理可将函数值与导数相衔接，本次计算过程中并未给出ξ具体位置，并且对于不等式来讲，可以不必做到精确。因此可以利用此种方法证明定理，主要在于选择f(x)以及区间[a，b]。

4 应用柯西中值定理解析不等式

在柯西定理中，加入f(x)，g(x)条件满足：1)在区间[a，b]连续；2)在区间[a，b]可导；3)f′(x)与g′(x)不在同一时段为0；4)g(a)≠g(b)。

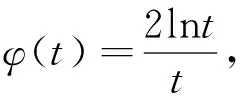
说明：柯西中值定理为探讨两个函数变量关系的中值关系定理，若函数为自变量时，便符合拉格朗日中值定理，因此可以利用拉格朗日中值定理解决的不等式也可以利用柯西中值定理处理，若相反则不能证明。

5 应用泰勒公式解析不等式

5.1 泰勒定理

1)函数在f(x)闭区间[a，b]中存在n阶连续导数。

2)f(x)在开区间[a，b]中存在f(x)的n+1阶导数，并且对x∈(a，b)存在一点ξ∈(a，b)。

5.2 泰勒公式证明不等式方法

1)据相关已知条件，确定证明目标，甄选合适的点将函数体现在泰勒公式中。

2)据已知条件，向较为有利证明目标不等式的方向做出合理计算，最终能够与已知条件结合，并将不等式结果证明。

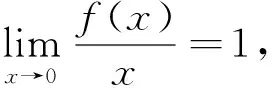
说明：将泰勒公式应用于解不等式中，应当根据题中假设条件选择计算函数，并在邻域将函数展开，将阶次及余项展开。

6 利用定积分原理解析不等式

说明：不等式中含有定积分，并且能够被积函数f(x)≤g(x)时，可以利用定积分性质将不等式解析。

7 结语

通过分析以上多种微积分方式解析不等式，可以发现存在一定条件时，不等式能够被顺利解题，并且不会存在较多困难。但是在实际解题过程中还应当做到具体问题具体分析，不等式证明不只是适用一种方式，可以通过多种证明方法将结果解析。