在对比中概括提升——“正比例的意义”教学实录与思考

◇杨灵君

一 填写表格，比较中概括意义

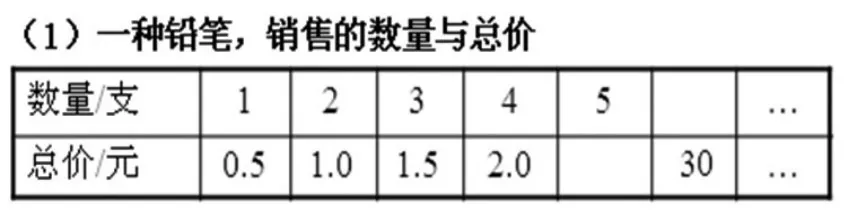
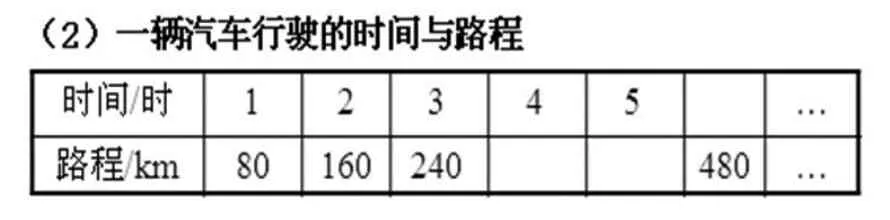
师：生活中总有“两种相关联的量，一种量变化，另一种量也随着变化”（板书），但有时的变化有规律，有时的变化没有规律，你能针对3张表格中两种相关联的量继续把表格填完整吗？

（预先发给每个学生如下的表格）

?

?

?

学生独立填表，很快填出了前两张，但在填第三张表格时碰到了困难。教师先让学生分组交流填表的想法，再组织集体反馈，并提出：第一张和第二张表格为什么你们能很快地填出来？而第三张为什么填写时有困难呢？

生：从第一张表格中可以看出数量和总价在增加，但每支铅笔的价钱都是0.5元。

师：每支铅笔的价钱都是0.5元，也就是单价不变。

生：从第二张表格中可以看出每小时行80千米，所以4小时就行320千米，5小时就行400千米，要行480千米就要6小时。

师：这里的时间与路程是相关联的两个量，路程随着行驶时间的变化而变化，从表格中可以看到这里的路程除以对应的时间等于速度，速度是不变的。

教师进一步指出：像以上两张表格中两种相关联的量，一种量变化，另一种量也随着变化，而且两种量中相对应的两个数量的比值一定，这样的两种量我们就叫作成正比例的量，它们的关系叫作正比例关系。教师板书正比例的意义，再让学生阅读课本，找出正比例意义的表述。接着教师根据学生的表述，写出字母式子

师：那第三张表格中，两种相关联的量有没有这样的变化规律呢？

生：没有。因为小明4岁时的身高一定比3岁时要高，但高多少不知道；5岁时的身高要比4岁时高，但高出多少也不知道，所以很不好填。

师：从表（3）前几格对应的几个数来看，身高随着年龄的增长也在增长，但每年增长数量不一样，而且他的身高到了一定年龄时也不会再增高。关键是年龄与身高这两种相关联的量中对应的两个数的比值在变化，所以说年龄与身高这两种量不能成正比例。

[教学思考]以上的学习素材中，表（1）就是原教材的例题，表（2）就是原教材“做一做”的练习素材，我把这两个素材放在一起，而且增加了表（3）不成正比例的两种量，其目的是使学生更好地投入自主探究。学生通过对前两张表格已有数据的观察和计算，发现了这两张表格中的两种相关联的量对应的两个数的比值是一定的，从中概括出正比例的意义。再让学生阅读教材，进一步理解正比例的意义。学生通过对第三张表格已有数据的观察，发现身高也随着年龄的增长而增长，但找不到规律。针对这张表格，我特别指出它们对应的两个数量的比值不相等，就不是成正比例的两种量。这样就给学生创设了对比素材，增强了对正比例意义的认识。

二 画图分析，观察中认识特征

1.针对教材例题中的图像回答问题。

师：书上已经根据表（1）的数据画出了图像的一部分，你能继续画图并回答问题吗？书上有如图1的图像和以下的几个问题。

（1）从图中你发现了什么？

（2）把数对（10，5.0）和（12，6.0）所在的点描出来，并和上面的图像连起来并延长，你还能发现什么？

（3）不计算，根据图像判断，如果买 7支铅笔总价是多少？20元能买多少支铅笔？

（4）小明买的铅笔的数量是小丽的2倍，他花的钱是小丽的几倍？

学生针对前两个问题回答出了总价随着支数的增加而增加，把每一点连在一起是一条直线。后两个问题大部分学生是通过计算作了回答，教师有意识地引导学生观察图像回答出：买7支铅笔的总价是3.5元。

对于20元可以买多少支铅笔，先引导学生通过图像的延长想象，再通过“20÷0.5”的计算得出可以买铅笔 40支。学生在思考第（4）个问题时，继续观察图像回答出“小明花的钱也是小丽的 2 倍”。（如图1）

图1

2.针对第二张表格继续在书上画图思考。

因为第二张表格就是教材第46页“做一做”的练习，此题只要求学生根据表格画好图像回答问题。（过程略）

[教学思考]学生通过对表（1）和表（2）图像的观察与思考，知道成正比例的两个相关联的量在图像上形成的是一条直线。在初步了解正比例图像的特征后，就可以通过对图像的观察，大致确定对应数对的点的位置，同时针对图像的分析，加深对正比例概念的理解。

三 创设练习，思考中深化认识

1.根据下面每张表格中的数据，判断表中两种相关联的量是否成正比例。

① 汽车所行路程和耗油量的对应数值表：

所行路程/km 36 72 108 144 …耗油量/L 2 4 6 8 …

② 同一时间、同一地点测得4棵树的树高和影长如下表：

树高/m 2 3 6 8 …影长/m 1.6 2.4 4.8 6.4 …

③ 在水果店里购买苹果的数量与总价如下表：

数量/kg 1 2 3 4 …总价/元 4 7 10.5 12 …

④ 在水果店里购买香梨的数量与总价如下表：

数量/kg 1 2 3 4 …总价/元 4 8 12 16 …

学生先独立思考，教师再组织集体交流。

师：还可以把以上对应的两个数量的比写成“耗油量∶所行的路程”，这样就可以得到什么是不变的？

生：每千米的耗油量是不变的。

师：所以同样可以说明所行的路程与耗油量成正比例。

接着，对第②张表格进行同样的分析。（略）

生：在第③张表中我发现买1千克要4元；如果要买2千克或3千克时，每千克的单价是3.5元；如果买4千克时，每千克的单价又是3元。这里的单价变化了，所以这张表中的总价与数量不能组成正比例。

生：在第④张表中发现不管买多少千克，单价都是4元，所以这张表中的总价与数量成正比例。

师：请你分别根据第③张和第④张表格中两种相关联量，在下面的格子纸上画出它们的图像。

当学生独立画图后，教师利用投影逐步呈现出它们的图像（图略）。并向学生提出：不能组成正比例和能组成正比例的图像有什么区别？

生：能组成正比例的图像是一条直线，不能组成正比例的这条线弯了。

[教学思考]这一环节给学生提供了4张表格，让学生再次观察分析表中两种相关联的量是否成正比例。通过学生的独立思考和集体交流，除了及时巩固对正比例意义的认识，还获得了演绎推理的训练。以上最后2张表虽然都分别呈现了两种水果购买数量与总价的变化情况，但学生从中发现表③的单价在变化，而表④的单价不变；再通过对图像的比较，强化了判断能否成正比例的关键和图像特征。

2.观察下面2张表格中两种相关联的量是否能成正比例。

① 正方形的边长与周长。

正方形的边长/c m 1 2 3 4 …正方形的周长/c m 4 8 1 2 1 6 …

② 正方形的边长与面积。

正方形的边长/c m 1 2 3 4 …正方形的面积/c m 1 4 9 1 6 …

教师再利用投影逐步呈现它们的图像（图略），再次引发学生观察周长与边长能成正比例的图像和面积与边长不能成正比例的图像的区别。

[教学思考]学生通过对正方形的边长与周长和正方形的边长与面积两种关系的判断，从图形角度再次认识正比例的意义和图像特征。

3.观察下面3张表格中两种相关联的量是否能成正比例。

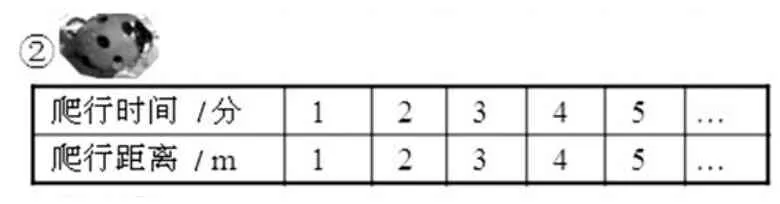
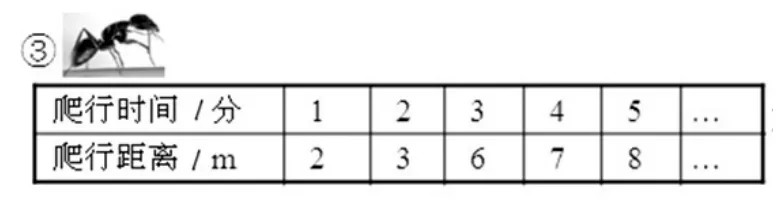
教师利用投影出示了如下的3张表格，这3张表格分别表示的是3只小动物爬行情况的记录。学生很有兴趣地观察后，教师组织集体质疑交流。

生：第一张表格是蜗牛爬行的，速度很慢，但速度都是相等的，所爬行的距离与爬行的时间成正比例。

生：第二张表格七星瓢虫爬行距离与爬行的时间也能成正比例。

生：第三张蚂蚁爬行的速度有快有慢，它爬行的距离与爬行的时间不能成正比例。

?

?

?

教师根据学生的回答在表格的右边打出判断的结果，接着又向学生提出：那你觉得怎样把蚂蚁爬行的距离改一改，使它爬行的距离与爬行的时间也能成正比例？

生：把蚂蚁爬2分钟的距离改成4m，爬4分钟的距离改为8m，爬5分钟的距离改为10m，这样蚂蚁爬行的距离与爬行的时间也能成正比例了。

教师根据学生的回答在投影上改动第三张表格中这几个数据，再向学生提出：现在这3只动物各自爬行的距离与爬行时间都成正比例了，我根据每一张表格画出了图（这时投影上呈现如图2），请大家继续观察表格和图，你又有什么发现？

生：我发现蜗牛爬得比较慢，画出的线比较平；蚂蚁爬得比较快，画出的线是最斜的。

师：你的意思是按第一张表格的对应数量画出的线上升的速度比较慢，按第三张表格的对应数量画出的线上升的速度比较快。

生：是的。

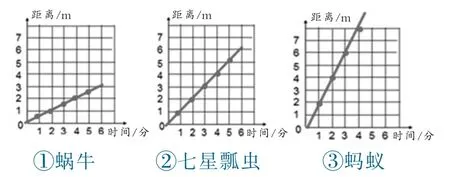
图2

这时教师在投影上又把以上三条线放在同一幅图上（图略），又向学生指出：从图中可明显地看出蚂蚁爬行的速度最快，画出的这条线是最陡的，而蜗牛爬行的速度最慢，画出的这条线是最平缓的。

[教学思考]由于上述表格和图都以小动物爬行的时间与爬行的距离为背景，学生自始至终颇有兴趣地参与其中，从而加深了对正比例意义的理解，同时较好地渗透了对应数量的比的值越大，所画出的线就越陡。这也正是在今后研究线性函数图像时的斜率大小问题。