区组为K4-e的可分组核心设计
高玉峰, 冯 弢
(1. 北京交通大学 理学院, 北京 100044; 2. 通化师范学院 数学学院, 吉林 通化 134000)
1 引言与预备知识
组合设计理论中的核心设计[1]在图分解、 图填充和图覆盖等问题中应用广泛. Mendelsohn等[1]首先提出了核心设计的概念, 并解决了区组长度为3核心设计的存在性问题. 本文将核心设计的概念推广到可分组核心设计.
设H是一个简单图,Γ是一个简单图的集合. 设X是H的点集, A,B是H子图的集合, A,B中的元素称为区组. 如果每个区组都同构于Γ中的一个图, 且H的每条边都包含在A的至多一个区组中, 则称(X,A)为一个(H,Γ)-填充. 如果每个区组都同构于Γ中的一个图, 且H的每条边都包含在B的至少一个区组中, 则称(X,B)为一个(H,Γ)-覆盖. 如果Γ只包含一个简单图G, 则记为(H,G)-填充或(H,G)-覆盖.
对于(H,G)-填充(X,A), 如果不存在(H,G)-填充(X,D)使得|D|>|A|, 则称该(H,G)-填充(X,A)是最大的. 由H中所有不包含在A区组中的边构成的图(X,L)称为(H,G)-填充(X,A)的余边图, 简称余边. 对于(H,G)-覆盖(X,B), 如果不存在(H,G)-覆盖(X,D)使得|D|<|B|, 则称该(H,G)-覆盖(X,B)是最小的. 由H中所有包含在B的至少两个区组中的边构成的图(X,E)称为(H,G)-覆盖(X,B)的超边图, 简称超边. 如果一个(H,G)-填充的余边是空的, 则该填充是最大的; 如果一个(H,G)-覆盖的超边是空的, 则该覆盖是最小的, 此时称为(H,G)-设计.
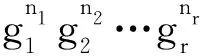
Billington等[2]给出了型为gn的K3-MGDP存在的充分必要条件, 并验证了所有可能的余边;Hu等[3]考虑带所有可能余边的型为gn的(K3+e)-MGDP存在性, 其中K3+e为三角K3带一条悬边, 解决了带所有可能超边的型为gn的(K3+e)-MGDC的存在性;Fort等[4]解决了型为1n的K3-MGDC的存在性问题;Heinrich等[5]推广了文献[4]的结果, 确定了型为gn的K3-MGDC存在的充分必要条件, 并给出了一种可能超边的存在性.
定义1设H,G为简单图, (X,A)为任意的最大(H,G)-填充, (X,B)为任意的最小(H,G)-覆盖, 令C=A∩B, 当|C|最大时, 称(X,C)为一个(H,G)-核心设计. 一个(Ku1,u2,…,ut,G)-核心设计称为可分组的G-核心设计, 记作型为{u1,u2,…,ut}的G-GDND.


这些边生成的所有可能余边列于表1.
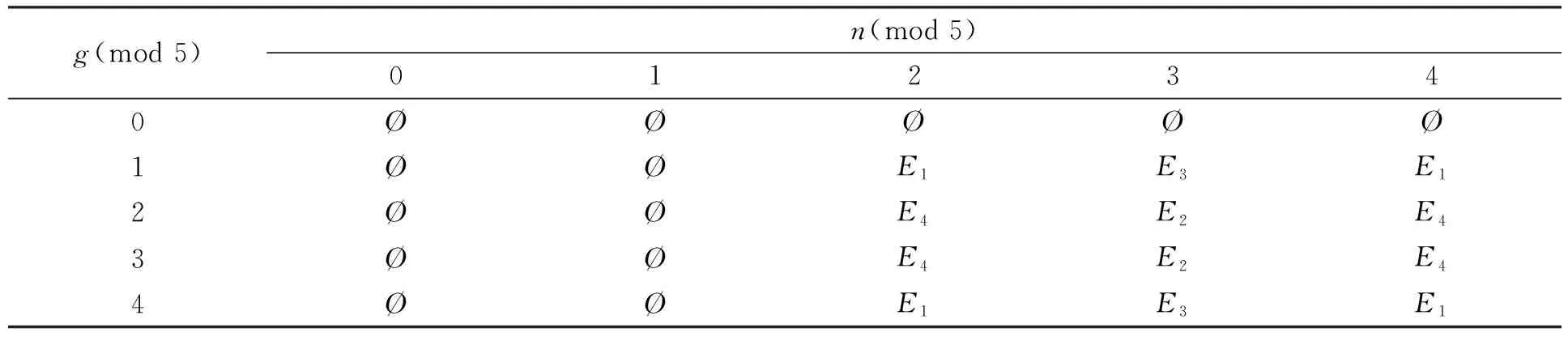
表1 组型为gn的(K4-e)-MGDP可能的余边
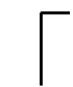
这些边生成所有可能的超边列于表2. 表1和表2中的Ei表示由i(i=1,2,3,4)条边组成的任意简单图. 易知E1为一条单边. 图1为E2,E3,E4所有可能的简单图, 其中Ei,j中的i(i=2,3,4)表示边数,j(1≤j≤11)为序号.

表2 组型为gn的(K4-e)-MGDC可能的超边

图1 含有2条边、 3条边、 4条边的简单图Fig.1 Simple graphs with 2 edges, 3 edges and 4 edges
Colbourn等[6]确定了型为gn的(K4-e)-GDD存在的充分必要条件;Hoffman等[7]研究了带所有可能余边的型为1n的(K4-e)-MGDP的存在性;Lindner等[8]给出了带所有可能超边的型为1n的(K4-e)-MGDC的存在性. 将型为gn的(K4-e)-GDND区组数记为N(gn), 由定义易知

本文利用直接构造和递归构造的方法, 讨论型为gn的(K4-e)-MGDP和(K4-e)-MGDC的存在性, 并确定型为gn的(K4-e)-GDND的存在性.
2 不完全可分组设计及相关构造
考虑两种不同结构的K4-e不完全可分组设计, 并讨论其在(K4-e)-GDND构造中的应用.
2.1 型为g(n,h)的K4-e不完全可分组设计
一个型为gn-h(gh)1的G-GDD称为一个型为g(n,h)的不完全G-GDD, 简写为型为g(n,h)的G-IGDD. 大小为gh的组称为IGDD的洞. 用一个型为gh的G-GDP填一个型为g(n,h)的G-IGDD的洞, 可得一个型为gn的G-GDP. 用一个型为gh的G-GDC填一个型为g(n,h)的G-IGDD的洞, 可得一个型为gn的G-GDC.
构造1假设存在型为g(n,h)的G-IGDD. 如果存在型为gh的G-GDND, 则可得型为gn的G-GDND.
证明: 设型为gh的G-GDND(X,C)是由型为gh的G-MGDP(X,A)和型为gh的G-MGDC(X,B)得到的, C=A∩B. 设型为g(n,h)的G-IGDD为(X,D). 用型为gh的G-MGDP(X,A)填型为g(n,h)的G-IGDD(X,D)的洞, 可得型为gn的G-MGDP(X,A∪D). 用型为gh的G-MGDC(X,B)填型为g(n,h)的G-IGDD(X,D)的洞, 可得型为gn的G-MGDC(X,B∪D). 用型为gh的G-GDND(X,C)填型为g(n,h)的G-IGDD(X,D)的洞, 可得(X,C∪D). 由
(A∪D)∩(B∪D)=(A∩B)∪D=C∪D
可知, (X,C∪D)是一个型为gn的G-GDND.
引理1[9]对于满足g(h+2)≡0(mod4)和h≡0(mod2)的任意正整数g,h, 总存在型为g((3h+2)/2,h)的(K4-e)-IGDD.
引理2[9]对于g,h∈{2,3,4}, 存在型为g(5+h,h)的(K4-e)-IGDD.
引理3[9]对于(g,n,h)∈{(2,14,7),(11,8,3)}, 存在型为g(n,h)的(K4-e)-IGDD.
构造2[9]假设存在型为g(n,h)的(K4-e)-IGDD, 则存在型为(gt)(n,h)的(K4-e)-IGDD, 其中t≥1.
对于n∈{12,14}, 型为1(n,4)的(K4-e)-IGDD是存在的[7], 由构造2可得如下引理.
引理4令n∈{12,14}, 对任意的g≥1, 总存在型为g(n,4)的(K4-e)-IGDD.
由文献[10]中可分组设计的标准填洞构造变形可得如下引理.
引理5[10]令n≡h(mod5), n≥15+h, 如果存在型为g(5+h,h)的(K4-e)-IGDD, 则存在型为g(n,5+h)和型为g(n,h)的(K4-e)-IGDD.
2.2 型为(g,h)n的K4-e的不完全可分组设计
令S为完全n部图Kn(g)点集的子集, S带分部的集合Gi(1≤i≤n), 满足|Gi∩S|=h. 令K[S]为由S诱导的Kn(g)的子图. 称(Kn(g)K[S],G)-设计为不完全的可分组设计, 记作型为(g,h)n的G-IGDD, S称为洞.
例1在I12上构造一个型为(4,1)3的(K4-e)-IGDD, 组为{i,i+3,i+6,i+9}, 0≤i≤2, 洞集合为S={0,1,2}. 所有的区组为: {[5,4,0-3],[7,8,0-6],[10,11,0-9],[5,6,1-10],[3,11,1-7],[8,9,1-4],[7,9,2-5],[3,10,2-8],[4,6,2-11]}.
类似构造1, 下面给出利用型为(g,h)n的G-IGDD构造G-GDND的基本方法.
构造3假设存在型为(g,h)n的G-IGDD. 如果存在型为hn的G-GDND, 则可得型为gn的G-GDND.
例2已知存在型为(4,1)4的(K4-e)-IGDD[9]和型为14的(K4-e)-GDND[7], 运用构造3可得型为44的(K4-e)-GDND.
构造4假设存在型为(g,h)n的(K4-e)-IGDD, 则存在型为(gt,ht)n的(K4-e)-IGDD, 其中t≥1.
引理6[9]令g≡r(mod5), g≥15+r, 如果存在型为(5+r,r)n的(K4-e)-IGDD, 则存在型为(g,5+r)n和型为(g,r)n的(K4-e)-IGDD.
引理7[9]令g(n-1)≡0(mod2), n≥3, 存在型为(3g,2g)n的(K4-e)-IGDD.
引理8[9]令n≥3, n≠6, 对于(g,h)∈{(4,1),(7,3),(13,7)}, 存在型为(g,h)n的(K4-e)-IGDD. 令n≥3, n≠6,8, 存在型为(11,1)n的(K4-e)-IGDD.
引理9[9]令r∈{2,3,4}, 存在型为(5+r,r)8的(K4-e)-IGDD. 令r∈{1,2,3,4}, n≥3, n≠6, 存在型为(5+r,r)n的(K4-e)-IGDD.
引理10[9]令n≡1,3(mod6), n≥3, 存在型为(11,6)n的(K4-e)-IGDD.
3 可分组核心设计的直接构造与递归构造
由核心设计定义可知, 如果由型为gn的(K4-e)-MGDP(X,A)和(K4-e)-MGDC(X,B)可得型为gn的(K4-e)-GDND(X,C), 则

因此, 假设由型为gn的(K4-e)-MGDP(X,A)和(K4-e)-MGDC(X,B)可得(X,C), C=A∩B, 如果

则此时|C|一定最大, 因此(X,C)是一个型为gn的(K4-e)-GDND. 如果

则此时|C|也一定最大, 因此(X,C)是一个型为gn的(K4-e)-GDND. 下面给出可分组设计的直接构造和递归构造.
1) g=1,2,3,4的情形.
引理11对于n∈{3,4,7,8,9,12,13,14}, 存在型为2n的(K4-e)-GDND.
证明: 令点集X=I2n, 组的集合为{{i,i+n}: 0≤i≤n-1}.
当n=3时, 已知带余边E2,1的型为23的(K4-e)-MGDP不存在, 带余边E2,2的型为23的(K4-e)-MGDP(X,A)存在, 且两条边的4个点只出现在两个组中[9]. 因此, 不能通过将A与一个区组求并的形式得到型为23的(K4-e)-MGDC. 所以, N(23)≤D(23)-1. 令
则|C|=|A|-1. 令
可知(X,A)是带余边E2,2的型为23的(K4-e)-MGDP, (X,B)是带超边E3,5的型为23的(K4-e)-MGDC, 则(X,C)是型为23的(K4-e)-GDND.
当n=4时, 令
可知(X,A)是带余边E4,2的型为24的(K4-e)-MGDP, (X,B)是带有超边E6的型为24的(K4-e)-MGDC, 则(X,C)是型为24的(K4-e)-GDND.
当n=7时, 令A=C, 区组为: {[0,8,6-13],[1,9,6-13],[2,10,6-13],[3,11,6-13],[4,12,6-13],[5,7,6-13],[0,2,4-5],[0,9,3-11],[0,1,10-12],[1,2,7-11],[1,5,3-4],[2,3,8-12],[4,7,3-10],[5,10,8-11],[8,9,4-7],[11,12,7-8]}. 令
B=C∪{[9,10,12-5]}, E4,1={{5,9},{9,10},{9,12},{10,12}}, E1={{5,10}}.
可知(X,A)是带余边E4,1的型为27的(K4-e)-MGDP, (X,B)是带超边E1的型为27的(K4-e)-MGDC, 则(X,C)是型为27的(K4-e)-GDND.
当n=8时, 令A=C, 区组为: {[0,3,2-4],[0,6,5-7],[0,10,9-11],[12,13,0-1],[14,15,0-1],[1,4,2-5],[1,6,3-10],[7,11,1-2],[2,8,5-6],[2,12,9-14],[13,15,2-3],[3,7,5-9],[9,15,5-6],[4,10,8-15],[10,12,3-7],[10,14,5-13],[4,14,9-11],[8,14,3-7],[4,13,6-7],[11,12,5-6],[9,13,8-11],[8,15,11-12]}. 令
可知(X,A)是带余边E2,1的型为28的(K4-e)-MGDP, (X,B)是带超边E3,2的型为28的(K4-e)-MGDC, 则(X,C)是型为28的(K4-e)-GDND.
当n=9时, 令A=C, 区组为: {[0,4,3-5],[0,7,6-8],[0,12,11-13],[14,15,0-1],[16,17,0-1],[1,5,3-6],[1,7,4-9],[8,12,1-2],[11,13,1-3],[2,6,3-4],[2,7,5-10],[2,13,9-16],[2,17,14-15],[3,14,7-8],[3,10,9-17],[15,16,3-4],[4,9,8-17],[10,12,4-6],[11,14,4-10],[5,15,8-12],[9,16,5-6],[10,13,5-15],[11,17,5-6],[6,13,8-14],[11,15,7-9],[7,17,12-13],[8,16,10-11],[12,14,9-16]}. 令
可知(X,A)是带余边E4,1的型为29的(K4-e)-MGDP, (X,B)是带超边E1的型为29的(K4-e)-MGDC, 则(X,C)是型为29的(K4-e)-GDND.
当n=12时, 令A=C, 区组为: {[0,4,5-6],[0,7,8-9],[0,10,11-13],[0,14,15-16],[0,17,18-19],[20,21,0-1],[22,23,0-1],[1,3,4-7],[1,6,5-17],[1,8,9-14],[1,10,12-15],[11,16,1-2],[18,19,1-2],[2,3,5-10],[4,8,2-10],[7,10,5-17],[9,10,6-18],[10,14,19-20],[10,16,21-23],[2,9,12-13],[2,15,6-17],[2,7,20-23],[21,22,2-3],[6,7,11-16],[4,7,12-14],[7,13,15-21],[18,22,4-7],[4,11,9-21],[4,13,17-19],[4,15,20-23],[5,9,14-15],[8,15,11-21],[12,15,16-18],[19,22,5-15],[5,18,8-21],[5,13,11-16],[5,12,20-23],[3,16,8-18],[11,14,3-18],[13,18,20-23],[12,19,11-21],[11,20,17-22],[16,22,9-17],[19,20,6-16],[8,23,17-19],[14,17,12-21],[6,23,14-21],[3,9,17-19],[20,23,3-9],[13,22,8-14],[6,12,8-22],[3,13,6-12]}. 令
可知(X,A)是带余边E4,1的型为212的(K4-e)-MGDP, (X,B)是带超边E1的型为212的(K4-e)-MGDC, 则(X,C)是型为212的(K4-e)-GDND.
当n=13时, 由引理1可知, h=8满足引理条件, 因此存在型为2(13,8)的(K4-e)-IGDD. 已知存在型为28的(K4-e)-GDND, 利用构造1可得型为213的(K4-e)-GDND. 当n=14时, 由引理3可知, 存在型为2(14,7)的(K4-e)-IGDD. 已知存在型为27的(K4-e)-GDND, 利用构造1可得型为214的(K4-e)-GDND.
引理12对于n∈{3,4,7,8,9,12,13,14}, 存在型为3n的(K4-e)-GDND.
证明: 令点集X=I3n, 组的集合为{{i,i+n,i+2n}: 0≤i≤n-1}.
当n=3时, 易知N(33)≤D(33)-1[9]. 由引理7可知, 存在型为(3,2)3的(K4-e)-IGDD. 由引理11可知, 存在型为23的(K4-e)-GDND, 应用构造3可得型为33的(K4-e)-GDND.
当n=4时, 令A=C, 区组为: {[0,3,5-6],[0,7,9-10],[1,3,4-10],[2,11,4-9],[3,8,2-9],[4,9,6-10],[5,7,2-4],[6,11,1-5],[7,8,1-6],[8,10,5-11]}. 令
可知(X,A)是带余边E4,1的型为34的(K4-e)-MGDP, (X,B)是带超边E1的型为34的(K4-e)-MGDC, 则(X,C)是型为34的(K4-e)-GDND.
当n∈{7,9,13}时, 由引理7可知, 存在型为(3,2)n的(K4-e)-IGDD. 由引理11可知, 存在型为2n的(K4-e)-GDND, 利用构造3可得型为3n的(K4-e)-GDND. 当n∈{12,14}时, 由引理4可知, 存在型为3(n,4)的(K4-e)-IGDD. 已知存在型为34的(K4-e)-GDND, 利用构造1可得型为3n的(K4-e)-GDND.
当n=8时, 令A=C, 区组为: {[0,2,1-3],[0,5,4-6],[0,9,7-10],[0,12,11-13],[0,15,14-17],[0,19,18-20],[0,22,21-23],[1,4,3-6],[1,7,5-8],[1,11,10-13],[1,14,12-16],[1,18,15-20],[19,22,1-2],[21,23,1-2],[2,7,4-6],[2,8,5-9],[2,14,11-13],[2,15,12-16],[17,20,2-3],[3,9,5-6],[3,10,7-8],[3,16,12-13],[14,21,3-4],[15,22,3-4],[18,23,3-4],[4,11,8-9],[4,13,10-17],[16,19,4-5],[5,12,10-17],[5,15,11-20],[14,23,5-8],[18,22,5-7],[6,13,8-15],[6,23,10-12],[6,18,11-16],[17,19,6-14],[20,21,6-11],[11,17,7-23],[7,21,12-16],[13,19,7-23],[14,20,7-10],[12,19,8-9],[15,21,8-9],[17,18,8-21],[20,22,8-13],[9,18,13-14],[16,22,9-11],[20,23,9-16],[10,19,15-21],[10,17,16-22]}. 令
可知(X,A)是带余边E2,1的型为38的(K4-e)-MGDP, (X,B)是带超边E3,3的型为38的(K4-e)-MGDC, 则(X,C)是型为38的(K4-e)-GDND.
引理13对于n∈{3,4,7,8,9,12,13,14}, 存在型为4n的(K4-e)-GDND.
证明: 令点集X=I4n, 组的集合为{{i,i+n,i+2n,i+3n}: 0≤i≤n-1}.
当n=3时, 令
可知(X,A)是带余边E3,1的型为43的(K4-e)-MGDP, (X,B)是带超边E2,1的型为43的(K4-e)-MGDC, 则(X,C)是型为43的(K4-e)-GDND.
当n=4时, 令A=C, 区组为: {[0,2,1-3],[0,6,5-7],[0,10,9-11],[0,14,13-15],[1,4,3-6],[1,8,7-10],[11,14,1-4],[12,15,1-2],[2,7,4-13],[5,11,2-12],[8,9,2-11],[5,10,3-7],[6,13,3-11],[8,14,3-5],[9,12,3-6],[4,15,5-9],[10,13,4-12],[8,15,6-13],[7,14,9-12]}. 令
B=C∪{[10,15,9-12]}, E1={{10,15}}, E4,2={{9,10},{9,15},{10,12},{12,15}}.
可知(X,A)是带余边E1的型为44的(K4-e)-MGDP, (X,B)是带超边E4,2的型为44的(K4-e)-MGDC, 则(X,C)是型为44的(K4-e)-GDND.
当n∈{7,9,12,14}时, 由引理1、 引理2和引理4可知, 存在型为4(n,4)的(K4-e)-IGDD. 已知存在型为44的(K4-e)-GDND, 利用构造1可得型为4n的(K4-e)-GDND. 当n=8时, 由引理2可知, 存在型为4(8,3)的(K4-e)-IGDD. 已知存在型为43的(K4-e)-GDND, 利用构造1可得型为48的(K4-e)-GDND. 当n=13时, 由引理1可知, 存在型为4(13,8)的(K4-e)-IGDD. 已知存在型为48的(K4-e)-GDND, 利用构造1可得型为413的(K4-e)-GDND.
引理14令g∈{1,2,3,4}, n≥3, 存在型为gn的(K4-e)-GDND.
证明: 对于g=1, 在Kn上讨论.
当n≡0,1(mod5), n≥6时, 型为1n的(K4-e)-设计即为(K4-e)-GDND. 当n≡2,3,4(mod5), n≥8且n≠9时, 易知存在型为1n的(K4-e)-GDND[7-8]. 此时,


对于g∈{2,3,4}, 当n≡0,1(mod5)时, 型为g6的(K4-e)-GDD即为(K4-e)-GDND.
当n≡2,3,4(mod5), 3≤n≤14时, 由引理11~引理13知结论成立. 此时,

当(g,n)∈{(2,3),(3,3)}时,


2) g=6,7,8,9,11,12,13,14的情形.
引理15对于n≥3, 存在型为6n的(K4-e)-GDND.
证明: 当n≥3时, 由引理7可知, 存在型为(6,4)n的(K4-e)-IGDD. 由引理14可知, 存在型为4n的(K4-e)-GDND. 利用构造3可得型为6n的(K4-e)-GDND.
引理16对于n≥3, 存在型为7n的(K4-e)-GDND.
证明: 令点集X=I7n, 组的集合为{{i,i+n,i+2n,i+3n,i+4n,i+5n,i+6n}: 0≤i≤n-1}.
当n=3时, 令A=C, 区组为: {[0,2,1-4],[0,7,5-8],[0,11,10-13],[0,16,14-17],[19,20,0-3],[1,5,3-6],[1,9,8-11],[1,14,12-15],[1,18,17-20],[2,10,3-12],[2,13,6-9],[2,18,7-19],[15,16,2-8],[3,14,4-7],[3,13,8-17],[11,16,3-18],[5,18,4-13],[4,11,6-15],[4,12,8-17],[9,20,4-7],[5,16,9-12],[5,15,10-19],[7,17,6-15],[6,19,8-14],[6,20,10-16],[11,12,7-19],[10,18,8-14],[9,17,10-19],[13,20,12-15]}. 令
可知(X,A)是带余边E2,1的型为73的(K4-e)-MGDP, (X,B)是带超边E3,3的型为73的(K4-e)-MGDC, 则(X,C)是型为73的(K4-e)-GDND.
当n=6时, 型为76的(K4-e)-GDD即为(K4-e)-GDND. 当n≥4, n≠6时, 由引理8可知, 存在型为(7,3)n的(K4-e)-IGDD. 由引理14可知, 存在型为3n的(K4-e)-GDND. 利用构造3可得型为7n的(K4-e)-GDND.
引理17对于n≥3, 存在型为8n的(K4-e)-GDND.
证明: 令点集X=I8n, 组的集合为{{i,i+n,i+2n,i+3n,i+4n,i+5n,i+6n,i+7n}: 0≤i≤n-1}.
当n=3时, 令A=C, 区组为: {[0,2,1-4],[0,7,5-8],[0,11,10-13],[0,16,14-17],[19,20,0-3],[22,23,0-3],[1,5,3-6],[1,9,8-11],[1,14,12-15],[1,18,17-20],[21,23,1-4],[2,7,3-6],[2,10,9-15],[12,13,2-20],[2,18,16-22],[19,21,2-11],[4,14,3-6],[8,10,3-12],[11,16,3-12],[13,17,3-6],[5,9,4-19],[4,18,8-11],[12,17,4-7],[15,20,4-22],[10,18,5-23],[5,22,12-21],[5,15,13-16],[6,22,8-11],[6,20,10-16],[19,23,6-12],[7,20,9-21],[7,15,11-23],[14,18,7-19],[8,21,13-16],[15,19,8-17],[9,23,13-16],[9,22,14-17],[10,21,14-17]}. 令
B=C∪{[14,18,13-16]}, E2,1={{13,14},{13,18}}, E3,1={{14,16},{14,18},{16,18}}.
可知(X,A)是带余边E2,1的型为83的(K4-e)-MGDP, (X,B)是带超边E3,1的型为83的(K4-e)-MGDC, 则(X,C)是型为83的(K4-e)-GDND.
当n=6时, 型为86的(K4-e)-GDD即为(K4-e)-GDND. 当n≥4, n≠6时, 由引理9可知, 存在型为(8,3)n的(K4-e)-IGDD. 由引理14可知, 存在型为3n的(K4-e)-GDND. 利用构造3可得型为8n的(K4-e)-GDND.
引理18对于n≥3, 存在型为9n的(K4-e)-GDND.
证明: 当n=6时, 型为96的(K4-e)-GDD即为(K4-e)-GDND. 当n≥3, n≠6时, 由引理9可知, 存在型为(9,4)n的(K4-e)-IGDD. 由引理14可知, 存在型为4n的(K4-e)-GDND. 利用构造3可得型为9n的(K4-e)-GDND.
引理19对于n≥3, 存在型为11n的(K4-e)-GDND.
证明: 当n=4或n≥10时, 由引理8和引理14可知, 存在型为(11,1)n的(K4-e)-IGDD和型为1n的(K4-e)-GDND, 利用构造3可得结论. 当n=5,6时, 型为11n的(K4-e)-GDD即为(K4-e)-GDND. 当n=3,7,9时, 由引理10和引理15可知, 存在型为(11,6)n的(K4-e)-IGDD和型为6n的(K4-e)-GDND, 利用构造3可得结论. 当n=8时, 由引理3可知, 存在型为11(8,3)的(K4-e)-IGDD和型为113的(K4-e)-GDND, 利用构造1可得结论.
引理20对于n≥3, g∈{12,14}, 存在型为gn的(K4-e)-GDND.
证明: 对于g∈{12,14}, 当n=6时, 型为g6的(K4-e)-GDD即为(K4-e)-GDND. 当n≥3, n≠6时, 令(g′,h′)∈{(6,4),(7,3)}, 由引理7和引理8可知, 存在型为(g′,h′)n的(K4-e)-IGDD. 由构造4可知, 存在型为(2g′,2h′)n的(K4-e)-IGDD. 由引理15和引理17可知, 存在型为(2h′)n的(K4-e)-GDND. 利用构造3可得型为gn的(K4-e)-GDND.
引理21对于n≥3, 存在型为13n的(K4-e)-GDND.
证明: 当n=6时, 型为136的(K4-e)-GDD即为(K4-e)-GDND. 当n≥3, n≠6时, 由引理8和引理16, 对于型为(13,7)n的(K4-e)-IGDD和型为7n的(K4-e)-GDND, 利用构造3可得型为13n的(K4-e)-GDND.
3) 任意g的情形.
引理22对于n≥3, g≡1,2,3,4(mod5), g≥16, 存在型为gn的(K4-e)-GDND.
证明: 当n=6时, 型为g6的(K4-e)-GDD即为(K4-e)-GDND. 当n≥3, n≠6时, 令r∈{1,2,3,4}, g≡r(mod5). 由引理9可知, 存在型为(5+r,r)n的(K4-e)-IGDD, 则由引理6可得型为(g,5+r)n的(K4-e)-IGDD. 由引理15~引理18可知, 存在型为(5+r)n的(K4-e)-GDND, 利用构造3可得结论.
综上, 由引理14~引理22可得本文主要结果如下:
定理1对于n≥3, g≥1, 存在型为gn的(K4-e)-GDND, 且
——平衡不完全区组设计定量资料一元方差分析

