g-期望的凸性及其应用*

纪荣林，周津名

(1. 安徽大学数学科学学院，安徽 合肥 230601；2. 合肥师范学院数学与统计学院，安徽 合肥 230601)

为了克服金融风险度量方法VaR的先天性缺陷，Artzner-Delbaen-Eber-Heath[1-2]首次通过公理化假设的方法开创性地引入了一致性风险度量的概念，随后 Föllmer-Schied[3]和 Frittelli-Rosazza Gianin[4]分别独立地提出凸风险度量的定义，即用条件较弱的凸性取代一致性风险度量公理化体系中的正齐次性和次可加性。 Detlefsen-Scandolo[5]引入了条件凸风险度量的定义，获得了条件凸风险度量可表示的充分必要性条件；进一步地，给出了动态凸风险度量定义并研究其时间相容性条件的等价刻画。关于动态凸风险度量的相关文章请参阅文献[6-9]等。众所周知，这种公理化的风险度量理论与非线性数学期望之间存在着紧密的联系。1997年，山东大学彭实戈院士通过非线性倒向随机微分方程的解引入了g-期望和条件g-期望的概念[10-11]。g-期望是一类典型的域流相容的非线性数学期望。Rosazza Gianin[12]将g-期望理论与公理化的金融风险度量结合起来，通过条件g-期望诱导出条件凸风险度量，进而通过g-期望诱导出一类时间相容的动态凸风险度量。Jiang[13]通过应用其所获得的倒向随机微分方程生成元的表示定理，系统性地建立了g-期望所诱导的 (动态) 凸风险度量与生成元函数g之间的一一对应关系。进一步地，Delbaen-Peng-Rosazza Gianin[14]应用g-期望所诱导的动态凸风险度量的表示结果给出了一类时间相容的动态凸风险度量(动态凹效用)的表示结果。

需要指出的是, Jiang[13]中动态凸风险度量的公理化假设，特别是在条件凸性假设上, 与 Detlefsen-Scandolo[5]是不一致的。由此，一个自然的问题是：在g-期望的框架下，关于动态凸风险度量的这两种定义方式是否是一致的？在倒向随机微分方程生成元满足基本假设条件的前提下，本文致力于研究 g-期望的凸性、条件凸性与生成元函数g之间的一一对应关系，进而证明这两种定义方式在g-期望框架下是等价的；进一步地，研究了g-期望与其诱导的时间相容的动态凸风险度量之间的对应关系。

1 预备知识

设T是一个给定的正实数，(Bt)t≥0是概率空间(Ω,F,P)上的d-维标准布朗运动，(Ft)t≥0是由该布朗运动生成的完备的σ域流。对每一个正整数n，记|·|为Rn中 Euclid 范数；对任意的z1,z2∈Rn，记z1·z2为向量z1与z2的内积；记L2(Ω,Ft,P)为Ft-可测且平方可积的随机变量全体; 记L∞(Ω,Ft,P)为Ft-可测且本性有界的随机变量全体。

考虑如下形式的一维倒向随机微分方程：

若生成元函数g:[0,T]×Ω×R×Rd→R满足下述假设条件 (A1) 和 (A2):

(A1) (Lipschitz条件) 存在常数K≥0使得dP×dt-a.s., 对任意的(y1,z1),(y2,z2)∈R×Rd有

|g(t,y1,z1)-g(t,y2,z2)|≤

K(|y1-y2|+|z1-z2|)

(A3) dP×dt-a.s., 对任意的y∈R有g(t,y,0)=0。

则由Pardoux-Peng[10]知, 对任意的ξ∈L2(Ω,FT,P), 上述倒向随机微分方程存在唯一一对平方可积的适应解，记为(Yt(g,T,ξ),Zt(g,T,ξ))t∈[0,T]。进一步地，若生成元函数g还满足假设条件(A3)，Peng[11]用Eg[ξ]表示Y0(g,T,ξ)，称Eg[ξ]为ξ的g-期望；用Eg[ξ|Ft]表示Yt(g,T,ξ)，并称Eg[ξ|Ft]为ξ关于Ft的条件g-期望。

接下来，我们引入本文的重要的引理，下述引理来自文献[13]的定理3.2。

引理1 设生成元g满足 (A1) 和 (A3)，则以下陈述等价：

(i)g独立于y且关于z是凸的，即对任意的z1,z2∈Rd，λ∈[0,1]，有

g(t,λz1+(1-λ)z2)≤

λg(t,z1)+(1-λ)g(t,z2),

dP×dt-a.s.

(ii) 对任意的X,Y∈L2(Ω,FT,P)，λ∈[0,1]，有

Eg[λX+(1-λ)Y]≤

λEg[X]+(1-λ)Eg[Y]

(iii) 对任意的t∈[0,T],X,Y∈L2(Ω,FT,P),λ∈[0,1], 有

Eg[λX+(1-λ)Y|Ft]≤

λEg[X|Ft]+(1-λ)Eg[Y|Ft],P-a.s.

为方便读者起见，我们回顾文献[5]中动态凸风险度量的公理化定义，如下：

定义1 称ρs,t(·):L∞(Ω,Ft,P)→L∞(Ω,Fs,P)，0≤s≤t≤T，为条件凸风险度量，若其在P-a.s.意义下满足：

(i) 单调性: 若X≥Y, 则ρs,t(X)≤ρs,t(Y)。

(ii) 平移不变性: 对任意的Y∈L∞(Ω,Fs,P), 有ρs,t(X+Y)=ρs,t(X)-Y。

(iii) 条件凸性: 对任意的λ∈L∞(Ω,Fs,P),λ∈[0,1],有

ρs,t(λX+(1-λ)Y)≤λρs,t(X)+(1-λ)ρs,t(Y)

(iv) 标准化:ρs,t(0)=0。

定义2 称 (ρs,t)0≤s≤t≤T为动态凸风险度量，若其对任意的0≤s≤t≤T，ρs,t(·)均为条件凸风险度量。进一步地，称动态凸风险度量(ρs,t)0≤s≤t≤T是时间相容的，若对任意的r∈[s,t]，X∈L∞(Ω,Ft,P)，有

ρs,t(X)=ρs,r(-ρr,t(X))

2 主要结果

定理1 设生成元g满足 (A1) 和 (A3), 则以下陈述等价：

(i)g独立于y且关于z是凸的, 即对任意的z1,z2∈Rd，λ∈[0,1]，有

g(t,λz1+(1-λ)z2)≤

λg(t,z1)+(1-λ)g(t,z2),dP×dt-a.s.

(ii)Eg[·]满足凸性，即对任意的X,Y∈L∞(Ω,FT,P)，λ∈[0,1]，有

Eg[λX+(1-λ)Y]≤λEg[X]+(1-λ)Eg[Y]

(iii)Eg[·|Ft] 满足条件凸性, 即对任意的t∈[0,T],X,Y∈L∞(Ω,FT,P),λ∈L∞(Ω,Ft,P),λ∈[0,1], 有

Eg[λX+(1-λ)Y|Ft]≤

λEg[X|Ft]+(1-λ)Eg[Y|Ft],P-a.s.

证明(iii)⟹(ii)是显然的。由引理1易证(ii)⟹(i)成立。下证 (i)⟹(iii)。首先, 考虑参数λ是简单函数时的情形，即

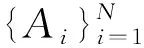
故对任意的 (y,z)∈R×Rd，

1Aig(t,y,z)=g(t,1Aiy,1Aiz),i=1,2,…,N

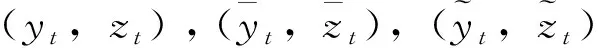
注意到对每一个i, 均有

从而

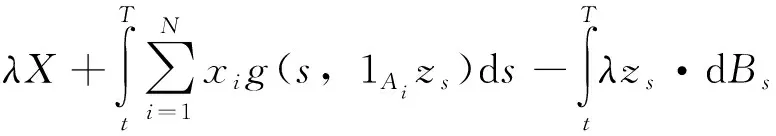
类似可得

Yt=λX+(1-λ)Y+

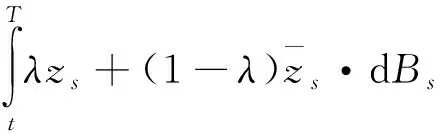
对每一个i=1,2,…,N，注意到g是独立于y且关于z是凸的, 结合xi∈[0,1], 可得

由g-期望的定义及倒向随机微分方程的比较定理立得

λEg[X|Ft]+(1-λ)Eg[Y|Ft]

接下来，考虑一般情形下的参数λ。对任意的λ∈L∞(Ω,Ft,P),λ∈[0,1]，选取L∞(Ω,Ft,P)中收敛于λ的简单函数列{λi}，其中对每一i，λi∈L∞(Ω,Ft,P)，λi∈[0,1]。由倒向随机微分方程解的连续依赖性(参阅Peng[11])知

EP[|Eg[λiX+(1-λi)Y|Ft]-

Eg[λX+(1-λ)Y|Ft]|2]≤

CT,KEP[|(λi-λ)(X-Y)|2]→0

其中，CT,K为仅依赖于T,K的非负常数。故对任意的t∈[0,T]，X,Y∈L∞(Ω,FT,P)，λ∈L∞(Ω,Ft,P)，λ∈[0,1]，有

Eg[λX+(1-λ)Y|Ft]≤

λEg[X|Ft]+(1-λ)Eg[Y|Ft],P-a.s.

证毕。

易验证, 对任意的X,Y∈L2(Ω,FT,P), 定理 1 中的论断依然成立, 结合引理1立得下述命题, 从而说明在g-期望的框架下, Jiang[13]中动态凸风险度量的公理化假设与Detlefsen-Scandolo[5]是完全一致的。

命题1 设生成元g满足 (A1) 和 (A3)，则以下陈述等价：

(i)Eg[·]是凸g-期望，即对任意的X,Y∈L2(Ω,FT,P)，λ∈[0,1]，有

Eg[λX+(1-λ)Y]≤

λEg[X]+(1-λ)Eg[Y]

(ii)Eg[·|Ft]满足条件凸性，即对任意的t∈[0,T]，X,Y∈L2(Ω,FT,P)，λ∈L2(Ω,Ft,P)，λ∈[0,1]，有

Eg[λX+(1-λ)Y|Ft]≤

λEg[X|Ft]+(1-λ)Eg[Y|Ft],P-a.s.

接下来, 我们探讨g-期望与其诱导的时间相容的动态凸风险度量之间的对应关系。

定理2 设生成元g满足 (A1) 和 (A3)。对任意的0≤s≤t≤T，令

则以下陈述等价:

(i)Eg[·]是凸g-期望。

(ii) (ρs,t)0≤s≤t≤T是时间相容的动态凸风险度量，且对任意的0≤s≤t≤T，ρs,t满足从上连续性，即若Xn↓X,P-a.s.，则ρs,t(Xn)↑ρs,t(X),P-a.s.

证明首先, 我们证明 (ii)⟹(i)成立。事实上，由(ρs,t)0≤s≤t≤T是动态凸风险度量知，对任意的t∈[0,T],ρt,T为条件凸风险度量。特别地，ρ0,T为凸风险度量。从而由凸风险度量的公理化定义知，对任意的X,Y∈L∞(Ω,FT,P),λ∈[0,1]，有

ρ0,T(λX+(1-λ)Y)≤

λρ0,T(X)+(1-λ)ρ0,T(Y)

结合ρ0,T(X)=Eg[-X|F0]=Eg[-X],∀X∈L∞(Ω,FT,P)，得

Eg[λ(-X)+(1-λ)(-Y)]≤

λEg[-X]+(1-λ)Eg[-Y],

∀X,Y∈L∞(Ω,FT,P)

即Eg[·]是凸g-期望。

下证 (i)⟹(ii)成立。对任意的0≤s≤t≤T，由定理 1 知生成元g独立于y且关于z是凸的，且条件g-期望Eg[·|Fs]满足条件凸性。进一步地，结合倒向随机微分方程的比较定理、解的存在唯一性，Peng[11]g-期望的平移不变性、保常数性、连续依赖性等，可知Eg[·|Fs] 在P-a.s. 意义下满足下述性质：

(a) 对任意的X,Y∈L∞(Ω,Ft,P), 若X≥Y, 则Eg[X|Fs]≥Eg[Y|Fs]。

(b) 对任意的X∈L∞(Ω,Ft,P),Y∈L∞(Ω,Fs,P), 有

Eg[X+Y|Fs]=Eg[X|Fs]+Y

(c) 对任意的X∈L∞(Ω,Ft,P),Y∈L∞(Ω,Fs,P),λ∈[0,1],有

Eg[λX+(1-λ)Y|Fs]≤

λEg[X|Fs]+(1-λ)Eg[Y|Fs],P-a.s.

(d)Eg[0|Fs]=0。

(e) 对任意的X∈L∞(Ω,Ft,P),r∈[s,t], 有

Eg[Eg[X|Fr]|Fs]=Eg[X|Fr∧s]=Eg[X|Fr]

(f) 若Xn,X∈L∞(Ω,Ft,P)且Xn→X, 则Eg[Xn|Fs]→Eg[X|Fs]。

由ρs,t(X)=Eg[-X|Fs],X∈L∞(Ω,Ft,P), 结合性质 (a)-(d) 可知ρs,t为条件凸风险度量, 且由性质 (a) 和 (f) 得，条件凸风险度量ρs,t满足从上连续性。进一步地，由时间参数s和t选取的任意性知，(ρs,t)0≤s≤t≤T是动态凸风险度量，从而由性质 (e) 立得 (ρs,t)0≤s≤t≤T是时间相容的动态凸风险度量。证毕。