B-C转捩模型的标定与应用*

余秋阳，邓小刚，包芸，王光学，王靖宇，张怀宝

(1.中山大学工学院，广东 广州 510006；2.国防科技大学空天科学学院，湖南 长沙 410073；3.中山大学物理学院，广东 广州 510006)

转捩现象的研究对飞行器设计非常重要。层流边界层和湍流边界层结构的不同会导致很多气动力参数在转捩后发生很大的变化。20世纪末，湍流模式理论显示出它在工程应用上的优势，很多模型如S-A模型[1]、k-ω模型[2]等涌现出来，全湍流的计算也得到了很多令人振奋的结果。但与此同时，转捩现象的数值模拟却没有得到很好的发展，原因可以归结为转捩现象本身的复杂性[3]：① 在于物理过程的复杂性。转捩的类型包括自然转捩、旁路转捩、分离诱导转捩等，同时湍流边界层在强顺压梯度下还可能再层流化，很难从一两个物理量的变化得到全部的物理信息。② 在于数学表达的复杂性。转捩流动中线性和非线性效应的相互影响导致几乎不可能用单一数学模型来刻画这一物理现象。

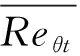
C转捩模型由Onur Bas和Samet等在2013年提出[13]。它与γ-Reθ模型一样基于当地关联。B-C模型使用函数公式而不是输运方程去激发转捩过程。它耦合于S-A湍流模型上使用，因其同样包含经验关联式，也可以根据不同的转捩关联进行标定。本文详细介绍了B-C转捩模型，利用零压力梯度平板转捩实验数据得到一组关联函数；并针对E387、NLF(1)-416翼型做了验证计算，将得到的结果与风洞实验结果、全湍流计算结果进行了比较，获得了有益的结论。

1 B-C转捩模型简介

非结构软件平台中的B-C转捩模型与文献[13]中的略有不同，修正了部分量纲不匹配的问题。间歇因子γ是转捩过程中流动状态的一个物理性质，整个转捩过程γ从层流状态时的0变为全湍流状态时的1。B-C转捩模型的思想就是建立一个间歇因子γ的表征函数用于实现转捩的数值模拟。S-A湍流模型的方程为：

(1)

B-C模型在原湍流模型生成项上乘上γ函数，从而达到在湍流计算中引入转捩的目的。

(2)

这样的转捩模型不会改变计算过程中的方程个数，形式上也较简单，这是它优于输运方程转捩模型之处。其中，γ函数的具体形式为：

(3)

(3)式由两部分组成：第一部分将涡雷诺数与转捩起始动量厚度雷诺数关联起来，起到判断转捩位置的作用；第二部分在近壁面区起作用。近壁面区涡雷诺数等于0，以至于第二部分也会等于0。第一部分使用的关联方法来源于文献[4]，其具体形式为：

(4)

(3)式中参数δ1=0.002，δ2=5.0，且

(5)

目前的B-C转捩模型使用的转捩动量厚度雷诺数表达式是一个与湍流强度相关的经验关联式[3]，即为：

Reθt=803.73(Tu+0.606 7)-1.027

(6)

2 B-C转捩模型标定过程

B-C转捩模型的标定是指利用T3系列低速平板实验的实验数据对模型中的经验关联式进行标定。B-C模型中的经验关联式只有Reθt的经验关联，原Reθt经验关联在B-C模型中不能很好地模拟转捩位置，与实验结果有所偏差，而，工程上更关心的是转捩位置，因此本文的标定工作主要依据转捩位置。本文采用与原有Reθt类似的样条拟合曲线，描述对Reθt的标定。

关联函数的标定一般选取低速平板实验中的S&K、T3A、T3A-和T3B。其中低湍流度的自然转捩有S&K和T3A-实验，高湍流度的旁路转捩有T3A和T3B实验。

标定过程中使用的网格如图1所示。网格数量为348×119，共41 412个矩形单元。网格在壁面处加密以保证边界层内的正确模拟。另外，在x=0处也加密了网格。标定计算在非结构软件平台上进行，对流项离散采用二阶精度的Roe格式，并使用预处理技术以适应低速流动。低速平板实验来流条件见表1, 表中FSTI为来流湍流强度。

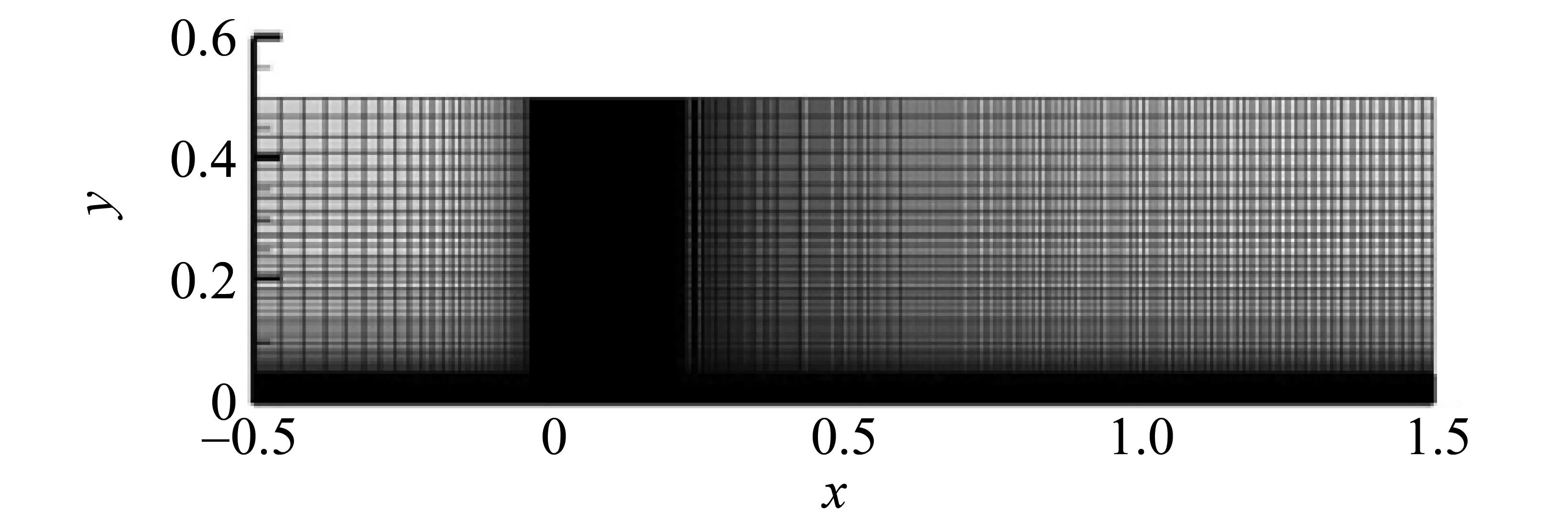
图1 平板计算网格Fig.1 Computational mesh for the flat plate

算例U/(m·s-1)μ/(Pa·s)ρ/(kg·m-3)FSTI/%S&K50.11.8×10-51.20.18T3A-19.81.8×10-51.20.874T3A5.41.8×10-51.23.5T3B9.41.8×10-51.26.5

关联函数Reθt的标定工作具体步骤如下所示：

1) 采用原有的Reθt经验关联式进行计算、并记录。将计算结果与实验值进行比较，若误差很小，则不再进行计算。

2) 对于步骤1)中误差较大的算例，需将Reθt定为常数代入计算。如果与实验值误差较大，则换另一常数代入计算。如此循环，直到计算值与实验值之间的误差很小为止。记录下最后的Reθt值。

3)记录步骤1)和步骤2)的所有Reθt值。新Reθt值与原Reθt值比较如表2所示。

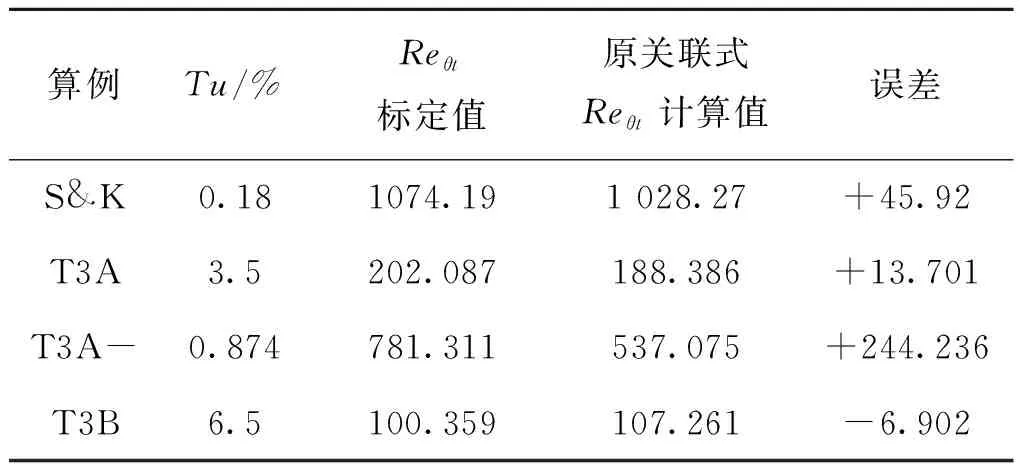
表2 平板算例的Tu和ReθtTable 2 Tu and Reθt of the flat plate

拟合表2中的数据得到新的经验关联式，如式(7)所示：

Reθt=-4.351Tu3+80.49Tu2-

502.705Tu+1 162

Tu≥0.027;Reθt≥20

(7)

原经验关联式曲线以及新经验关联式曲线，如图2所示。

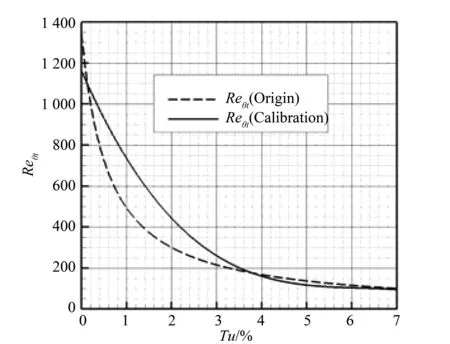
图2 经验关联式与计算值的对比Fig.2 The comparison of empirical correlation and calculated value

标定后的B-C转捩模型的低速平板算例的计算结果如图3-6所示。

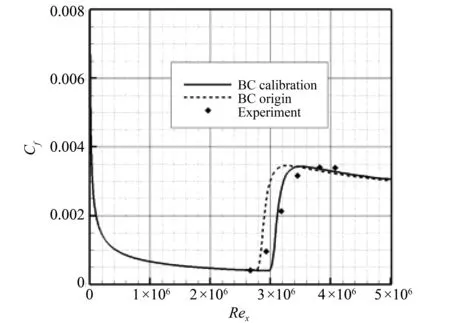
图3 S&K平板算例的计算结果Fig.3 Calculation result of S&K flat plate

图4 T3A平板算例的计算结果Fig.4 Calculation result of T3A flat plate

图5 T3A-平板算例的计算结果Fig.5 Calculation result of T3A- flat plate

图6 T3B平板算例的计算结果Fig.6 Calculation result of T3B flat plate

3 标定后的B-C转捩模型在二维低速问题上的应用

3.1 低雷诺数算例

Eppler E387翼型的转捩仿真是典型的低雷诺数翼型转捩算例。低雷诺数下的翼型绕流问题十分复杂，通常会有分离泡[14]，影响转捩的因素也较多。本文选取E387翼型在雷诺数为2×105和3×105时的流动，对本文的标定模型进行验证计算。算例采用O网格构型，共129 870个单元，如图7所示。网格在翼面附近加密，第一层网格控制在10-6量级以保证y+<1。

图7 E387翼型算例的网格图Fig.7 Mesh of E387 airfoil

本算例来流湍流强度FSTI=0.1%，对流项离散采用二阶精度的Roe格式，时间离散采用欧拉隐式格式，离散方程采用LU-SGS方法求解。为了更好的模拟低速情况，加快算法的收敛，本文采用了预处理技术。本文根据气动力参数的计算结果，绘制了升力系数曲线和极曲线，分析了升阻力系数的变化趋势。最后，将转捩模型的计算结果与全湍流模型计算结果、实验结果进行了对比分析，实验结果取自文献[13]。当计算攻角α从-3°增大到12°时，Re分别为2×105和3×105的升力系数、极曲线如图8-9所示。

从图中可以看出，在不同雷诺数下，转捩模型的计算结果都明显优于全湍流模型。全湍流模型可以很好地模拟升力系数，但阻力系数却与实验结果相差较大，可见转捩现象的影响在气动力参数计算上的重要性。另外，还可以发现不管是升力变化还是极曲线的计算结果与实验结果都很吻合。随着攻角的不断增大，超过失速角后，可能是由于流动分离过大，转捩模型的计算结果会出现偏差。

图9 Re=3×105时的升力系数和极曲线Fig.9 Lift coefficient and polar curve at Re=3×105

3.2 中高雷诺数算例

NASA/LANGLEY NLF(1)-416翼型被广泛应用于转捩模型的测试计算[13、15]。NLF(1)-416算例的实验结果取自文献[13]。本文计算了Re=1×106和2×106两种工况，来流湍流强度为0.03%。本算例的网格采用C型结构网格，共189 945个单元，如图10所示。翼面上分布了1 048个网格点，网格在翼面附近和尾迹区加密，翼面上第一层网格高度设为1×10-5以保证y+<1。

图10 NLF(1)-416翼型算例的网格图Fig.10 Mesh of NLF(1)-416 airfoil

3.2.1 气动力参数 本算例采用与E387翼型一样的计算方法与离散格式。当计算攻角α从-6°增大到12°时，Re分别为1×106和2×106的升力系数、极曲线如图11-12所示。

从图11-12可以看出， 对于在不同雷诺数工况下的NLF(1)-416翼型来说，转捩模型的计算结果同样都明显优于全湍流模型，更加符合实际流动。从升力系数和极曲线的变化趋势来看，转捩模型的计算结果与实验结果大致相同。

3.2.2 摩阻系数分布 6°攻角下摩阻系数计算结果如图13-14所示。

图13-14将转捩模型的计算结果与全湍流模型进行了对比。根据摩阻系数变化趋势可以判断流动是否发生了层流分离。当摩阻系数沿弦向先降为负值时，说明出现了回流即发生层流分离；然后，摩阻系数迅速增长为正值，说明分离导致转捩并且湍流又附着到物面上。从图13中可以看出：在Re=1×106的工况下，上翼面在翼型弦长32.7%处发生了分离，在40%处再附着；下翼面在在翼型弦长61%处发生分离，在68.5%处再附着。从图14处可以看出：在Re=2×106的工况下，上翼面没有发生流动分离现象，下翼面分离点位于翼型弦长61%处，再附着点位于65.7%处。由摩阻系数计算结果可以看出转捩模型的计算结果可以体现层流分离泡在中高雷诺数翼型转捩过程中的影响。

图11 Re=1×106时的升力系数和极曲线Fig.11 Lift coefficient and polar curve at Re=1×106

图12 Re=2×106时的升力系数和极曲线Fig.12 Lift coefficient and polar curve at Re=2×106

4 结 论

本文确定了一组经验关联函数，并且在低速平板算例中的摩阻系数分布与实验结果吻合得很好，说明了本文的标定工作是成功的；在二维低速问题中对比了标定后的B-C转捩模型和全湍流模型，选择了中低雷诺数两个算例。计算结果表明标定后的B-C转捩模型可以很好地捕捉转捩过程，中等攻角下计算出的升力阻力系数与实验结果吻合得较好。标定后的B-C转捩模型还可以反映层流分离泡在中高雷诺数翼型转捩过程中的影响。这些都说明了B-C转捩模型的合理性。

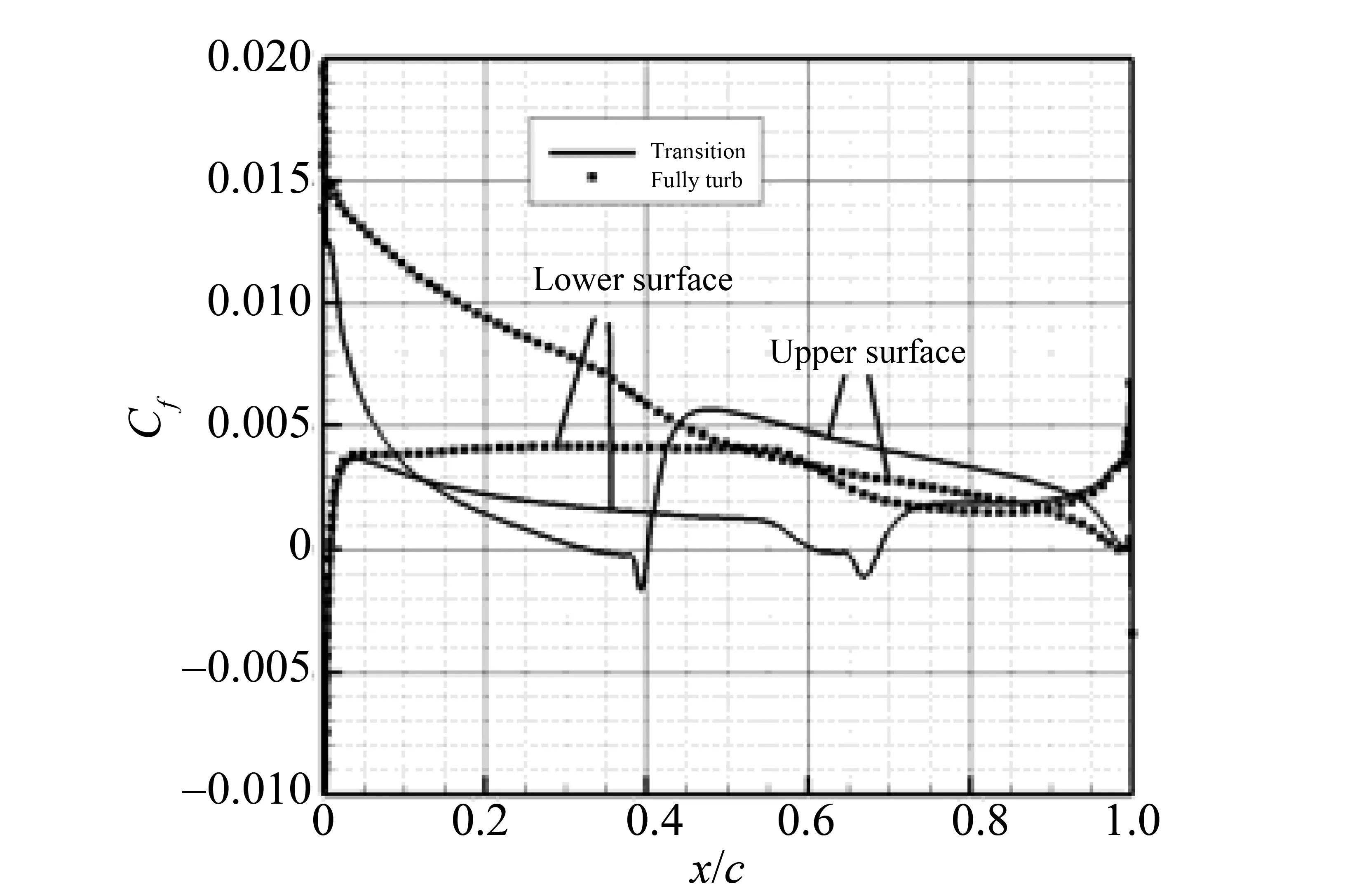
图13 Re=1×106时的摩阻系数计算结果Fig.13 Frictions coefficient around the airfoil at Re=1×106

图14 Re=2×106时摩阻系数计算结果Fig.14 Frictions coefficient around the airfoil at Re=1×106